湘教版八年级数学上册第2章三角形 单元测试 (含答案)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形 单元测试 (含答案) | 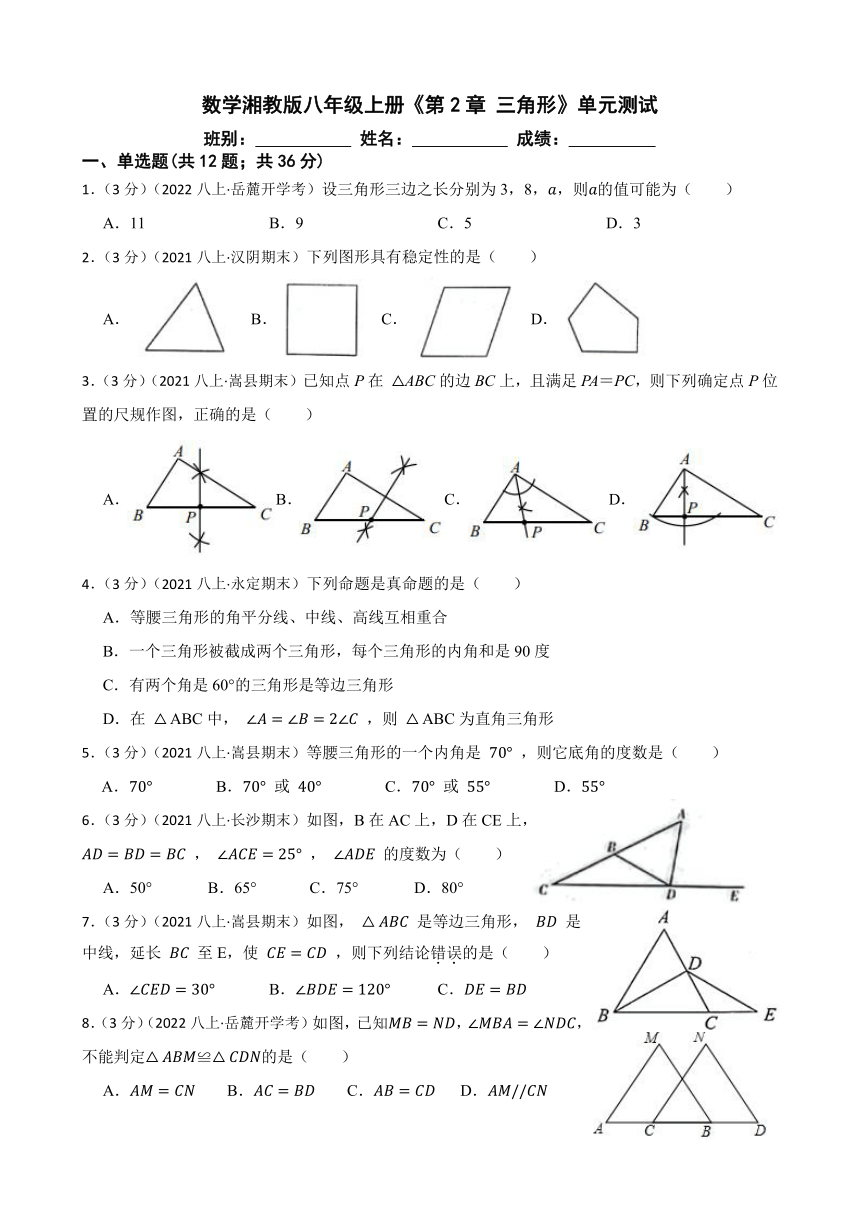 | |
| 格式 | docx | ||
| 文件大小 | 242.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 13:14:50 | ||
图片预览



文档简介
数学湘教版八年级上册《第2章 三角形》单元测试
班别: 姓名: 成绩:
一、单选题(共12题;共36分)
1.(3分)(2022八上·岳麓开学考)设三角形三边之长分别为3,8,,则的值可能为( )
A.11 B.9 C.5 D.3
2.(3分)(2021八上·汉阴期末)下列图形具有稳定性的是( )
A. B. C. D.
3.(3分)(2021八上·嵩县期末)已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A.B.C.D.
4.(3分)(2021八上·永定期末)下列命题是真命题的是( )
A.等腰三角形的角平分线、中线、高线互相重合
B.一个三角形被截成两个三角形,每个三角形的内角和是90度
C.有两个角是60°的三角形是等边三角形
D.在 ABC中, ,则 ABC为直角三角形
5.(3分)(2021八上·嵩县期末)等腰三角形的一个内角是 ,则它底角的度数是( )
A. B. 或 C. 或 D.
6.(3分)(2021八上·长沙期末)如图,B在AC上,D在CE上,
, , 的度数为( )
A.50° B.65° C.75° D.80°
7.(3分)(2021八上·嵩县期末)如图, 是等边三角形, 是中线,延长 至E,使 ,则下列结论错误的是( )
A. B. C. D.
8.(3分)(2022八上·岳麓开学考)如图,已知,,不能判定≌的是( )
A. B. C. D.
9.(3分)(2021八上·南充期末)如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( )
A. B.
C. D.
10.(3分)(2021八上·嵩县期末)如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A. B. C. D.
11.(3分)(2021八上·长沙期末)如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )
A.7 B.8 C.10 D.12
12.(3分)(2022八上·岳麓开学考)如图,已知平分,于,,则下列结论:;;;;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共18分)
13.(3分)(2022八上·岳麓开学考)将一副直角三角板如图放置,使含角的三角板的短直角边和含角的三角板的一条直角边重合,则的度数为 .
14.(3分)(2021八上·南京期末)如图,在 ABC中,AB=AC,∠A=36°,点D在AC上,且BD=BC,则∠BDC= .
15.(3分)(2021八上·嵩县期末)若 ,则以a、b为边长的等腰三角形的周长为 .
16.(3分)(2021八上·河南期末)“的算术平方根是2”这个命题是 命题.(填“真”或者“假”)
17.(3分)(2021八上·永定期末)在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为 .
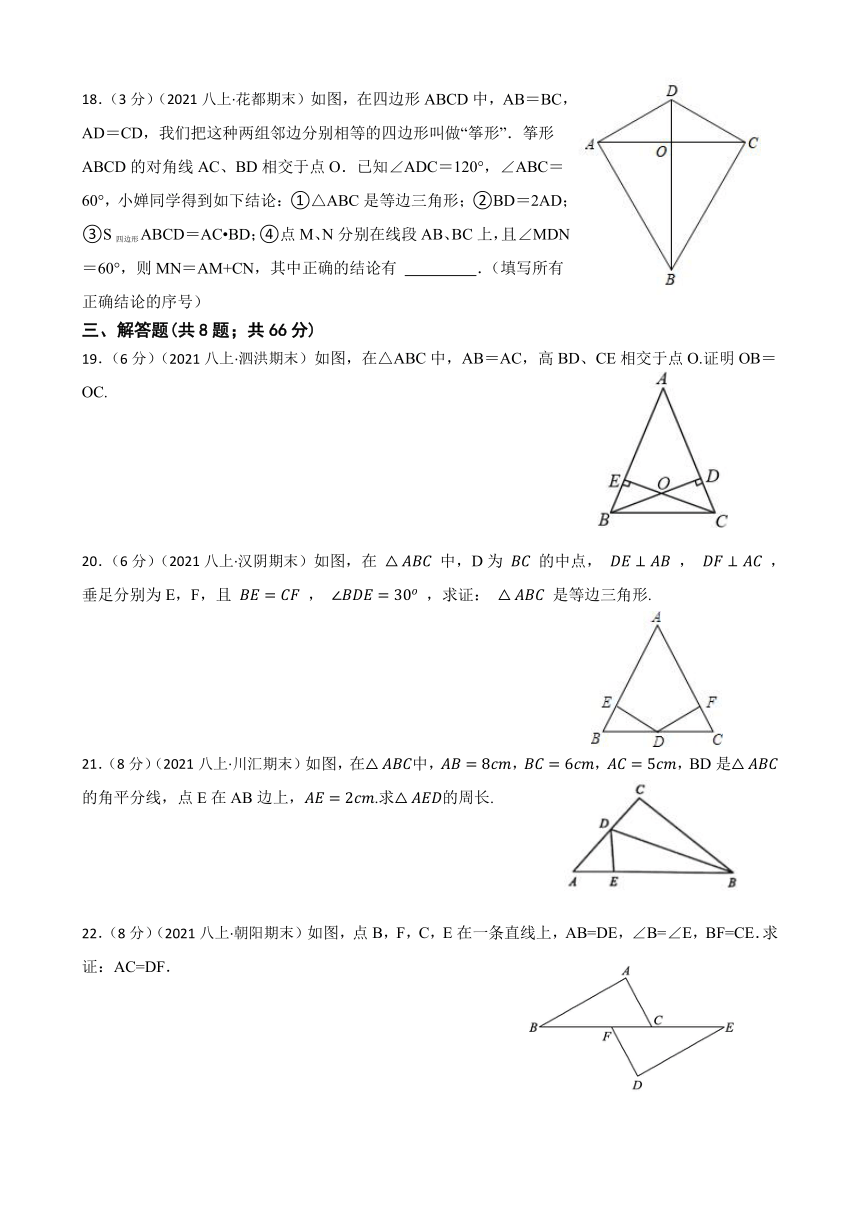
18.(3分)(2021八上·花都期末)如图,在四边形ABCD中,AB=BC,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC、BD相交于点O.已知∠ADC=120°,∠ABC=60°,小婵同学得到如下结论:①△ABC是等边三角形;②BD=2AD;③S四边形ABCD=AC BD;④点M、N分别在线段AB、BC上,且∠MDN=60°,则MN=AM+CN,其中正确的结论有 .(填写所有正确结论的序号)
三、解答题(共8题;共66分)
19.(6分)(2021八上·泗洪期末)如图,在△ABC中,AB=AC,高BD、CE相交于点O.证明OB=OC.
20.(6分)(2021八上·汉阴期末)如图,在 中,D为 的中点, , ,垂足分别为E,F,且 , ,求证: 是等边三角形.
21.(8分)(2021八上·川汇期末)如图,在中,,,,BD是的角平分线,点E在AB边上,.求的周长.
22.(8分)(2021八上·朝阳期末)如图,点B,F,C,E在一条直线上,AB=DE,∠B=∠E,BF=CE.求证:AC=DF.
23.(8分)(2021八上·南京期末)已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
24.(8分)(2021八上·岳阳期末)已知:如图,点B,F在线段EC上, , , .求证: .
25.(10分)(2021八上·泰州月考)已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
26.(12分)(2021八上·平凉期中)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)(4分)当∠BAD=60°时,求∠CDE的度数;
(2)(4分)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)(4分)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
答案解析部分
1.【答案】B 2.【答案】A 3.【答案】B 4.【答案】C 5.【答案】C 6.【答案】C
7.【答案】D 8.【答案】A 9.【答案】D 10.【答案】A 11.【答案】C 12.【答案】C
13.【答案】165° 14.【答案】72° 15.【答案】17
16.【答案】假 17.【答案】6 18.【答案】①②④
19.【答案】证明:∵ ,
∴ ,
又∵ 是 的高,
∴ ,
∴ 在 和 中,
,
∴ ( ),
∴ ,
∴ .
20.【答案】证明:∵ , ,
∴∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD,
∴∠B=∠C,
∴AB=AC,
∵ ,
∴∠B=60°,
是等边三角形.
21.【答案】解:∵,,,
∴,
∵BD是的角平分线,
∴,
在和中,
,
∴,
∴,
∵,
∴的周长.
22.【答案】证明:∵BF= CE,∴BC= EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
∴AC=DF.
23.【答案】证明:如图,记的交点为O,
∵∠ABC=∠DCB,∠1=∠2,
又∵∠OBC=∠ABC ∠1,∠OCB=∠DCB ∠2,
∴∠OBC=∠OCB,
∴OB=OC,
在△ABO和△DCO中,,
∴△ABO≌△DCO(ASA),
∴AB=DC.
24.【答案】证明:∵ ,
∴ ,
∵ ,
∴ ,即 ,
在 与 中,
,
∴ ,
∴ ,
∴ .
25.【答案】解:如图,连接AP、CP,
∵BP平分∠ABC,PD⊥AB,PE⊥BC,
∴∠PBD=∠PBE,∠PDB=∠PEC=90°,PD=PE,
在△BPD和△BPE中,
,
∴△BPD≌△BPE(AAS),
∴BD=BE,
又∵BE=10cm,AB=6cm,
∴AD=BD﹣AB=BE﹣AB=4cm,
∵PQ垂直平分AC,
∴PA=PC,
在Rt△PAD和Rt△PCE中,
,
∴Rt△PAD≌Rt△PCE(HL),
∴CE=AD=4cm.
26.【答案】(1)解:∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED-∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°﹣x,
∵AE=AD,
∴∠AED=45°+ ,
∴∠CDE= ;
∠CDE= ∠BAD
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°﹣2y,
∵∠BAD=x,
∴∠DAE=y+ ,
∴ .
∠CDE= ∠BAD
班别: 姓名: 成绩:
一、单选题(共12题;共36分)
1.(3分)(2022八上·岳麓开学考)设三角形三边之长分别为3,8,,则的值可能为( )
A.11 B.9 C.5 D.3
2.(3分)(2021八上·汉阴期末)下列图形具有稳定性的是( )
A. B. C. D.
3.(3分)(2021八上·嵩县期末)已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A.B.C.D.
4.(3分)(2021八上·永定期末)下列命题是真命题的是( )
A.等腰三角形的角平分线、中线、高线互相重合
B.一个三角形被截成两个三角形,每个三角形的内角和是90度
C.有两个角是60°的三角形是等边三角形
D.在 ABC中, ,则 ABC为直角三角形
5.(3分)(2021八上·嵩县期末)等腰三角形的一个内角是 ,则它底角的度数是( )
A. B. 或 C. 或 D.
6.(3分)(2021八上·长沙期末)如图,B在AC上,D在CE上,
, , 的度数为( )
A.50° B.65° C.75° D.80°
7.(3分)(2021八上·嵩县期末)如图, 是等边三角形, 是中线,延长 至E,使 ,则下列结论错误的是( )
A. B. C. D.
8.(3分)(2022八上·岳麓开学考)如图,已知,,不能判定≌的是( )
A. B. C. D.
9.(3分)(2021八上·南充期末)如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( )
A. B.
C. D.
10.(3分)(2021八上·嵩县期末)如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A. B. C. D.
11.(3分)(2021八上·长沙期末)如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )
A.7 B.8 C.10 D.12
12.(3分)(2022八上·岳麓开学考)如图,已知平分,于,,则下列结论:;;;;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共18分)
13.(3分)(2022八上·岳麓开学考)将一副直角三角板如图放置,使含角的三角板的短直角边和含角的三角板的一条直角边重合,则的度数为 .
14.(3分)(2021八上·南京期末)如图,在 ABC中,AB=AC,∠A=36°,点D在AC上,且BD=BC,则∠BDC= .
15.(3分)(2021八上·嵩县期末)若 ,则以a、b为边长的等腰三角形的周长为 .
16.(3分)(2021八上·河南期末)“的算术平方根是2”这个命题是 命题.(填“真”或者“假”)
17.(3分)(2021八上·永定期末)在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为 .
18.(3分)(2021八上·花都期末)如图,在四边形ABCD中,AB=BC,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC、BD相交于点O.已知∠ADC=120°,∠ABC=60°,小婵同学得到如下结论:①△ABC是等边三角形;②BD=2AD;③S四边形ABCD=AC BD;④点M、N分别在线段AB、BC上,且∠MDN=60°,则MN=AM+CN,其中正确的结论有 .(填写所有正确结论的序号)
三、解答题(共8题;共66分)
19.(6分)(2021八上·泗洪期末)如图,在△ABC中,AB=AC,高BD、CE相交于点O.证明OB=OC.
20.(6分)(2021八上·汉阴期末)如图,在 中,D为 的中点, , ,垂足分别为E,F,且 , ,求证: 是等边三角形.
21.(8分)(2021八上·川汇期末)如图,在中,,,,BD是的角平分线,点E在AB边上,.求的周长.
22.(8分)(2021八上·朝阳期末)如图,点B,F,C,E在一条直线上,AB=DE,∠B=∠E,BF=CE.求证:AC=DF.
23.(8分)(2021八上·南京期末)已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
24.(8分)(2021八上·岳阳期末)已知:如图,点B,F在线段EC上, , , .求证: .
25.(10分)(2021八上·泰州月考)已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
26.(12分)(2021八上·平凉期中)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)(4分)当∠BAD=60°时,求∠CDE的度数;
(2)(4分)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)(4分)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
答案解析部分
1.【答案】B 2.【答案】A 3.【答案】B 4.【答案】C 5.【答案】C 6.【答案】C
7.【答案】D 8.【答案】A 9.【答案】D 10.【答案】A 11.【答案】C 12.【答案】C
13.【答案】165° 14.【答案】72° 15.【答案】17
16.【答案】假 17.【答案】6 18.【答案】①②④
19.【答案】证明:∵ ,
∴ ,
又∵ 是 的高,
∴ ,
∴ 在 和 中,
,
∴ ( ),
∴ ,
∴ .
20.【答案】证明:∵ , ,
∴∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD,
∴∠B=∠C,
∴AB=AC,
∵ ,
∴∠B=60°,
是等边三角形.
21.【答案】解:∵,,,
∴,
∵BD是的角平分线,
∴,
在和中,
,
∴,
∴,
∵,
∴的周长.
22.【答案】证明:∵BF= CE,∴BC= EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
∴AC=DF.
23.【答案】证明:如图,记的交点为O,
∵∠ABC=∠DCB,∠1=∠2,
又∵∠OBC=∠ABC ∠1,∠OCB=∠DCB ∠2,
∴∠OBC=∠OCB,
∴OB=OC,
在△ABO和△DCO中,,
∴△ABO≌△DCO(ASA),
∴AB=DC.
24.【答案】证明:∵ ,
∴ ,
∵ ,
∴ ,即 ,
在 与 中,
,
∴ ,
∴ ,
∴ .
25.【答案】解:如图,连接AP、CP,
∵BP平分∠ABC,PD⊥AB,PE⊥BC,
∴∠PBD=∠PBE,∠PDB=∠PEC=90°,PD=PE,
在△BPD和△BPE中,
,
∴△BPD≌△BPE(AAS),
∴BD=BE,
又∵BE=10cm,AB=6cm,
∴AD=BD﹣AB=BE﹣AB=4cm,
∵PQ垂直平分AC,
∴PA=PC,
在Rt△PAD和Rt△PCE中,
,
∴Rt△PAD≌Rt△PCE(HL),
∴CE=AD=4cm.
26.【答案】(1)解:∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED-∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°﹣x,
∵AE=AD,
∴∠AED=45°+ ,
∴∠CDE= ;
∠CDE= ∠BAD
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°﹣2y,
∵∠BAD=x,
∴∠DAE=y+ ,
∴ .
∠CDE= ∠BAD
同课章节目录
