湘教版八年级数学上册第2章三角形2.1—2.3培优试题 (含答案)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形2.1—2.3培优试题 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 863.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 13:17:54 | ||
图片预览




文档简介
第2章《三角形2.1—2.3》培优试题2022-2023学年湘教版八年级数学上册
一.选择题(共10小题,每小题3分,共30分)
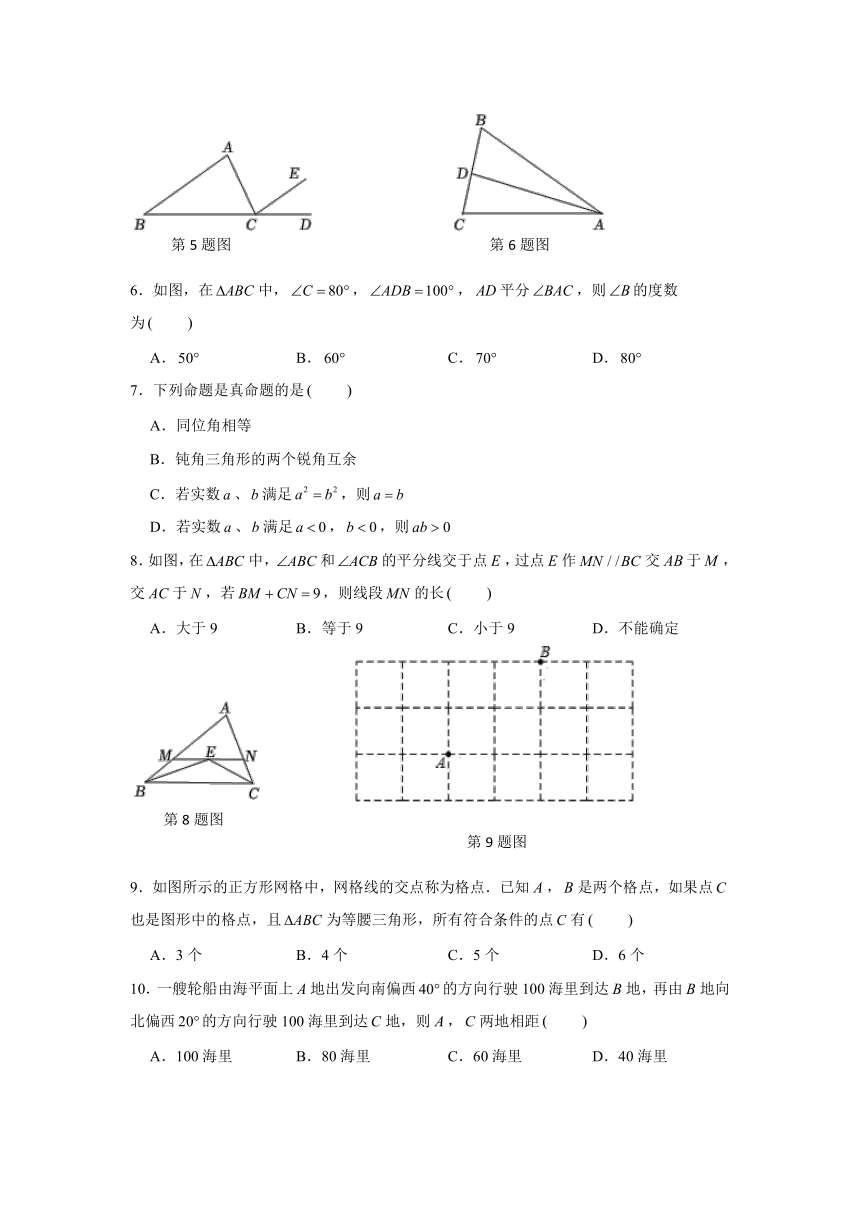
1.如图,以为边的三角形的个数是
A.1个 B.2个 C.3个 D.4个
(
第
2
题图
)
(
第
1
题图
)
2.下列关于三角形的分类,有如图所示的甲、乙两种分法,则
A.甲、乙两种分法均正确 B.甲分法正确,乙分法错误
C.甲分法错误,乙分法正确 D.甲、乙两种分法均错误
3.下列各组图形中,是的高的图形是
A. B.
C. D.
4.下列长度的三条线段能组成三角形的是
A.3,4,8 B.5,6,11 C.5,6,10 D.4,4,9
5.如图,是的外角,,,,则的度数为
A. B. C. D.
(
第
6
题图
) (
第
5
题图
)
6.如图,在中,,,平分,则的度数
为
A. B. C. D.
7.下列命题是真命题的是
A.同位角相等
B.钝角三角形的两个锐角互余
C.若实数、满足,则
D.若实数、满足,,则
8.如图,在中,和的平分线交于点,过点作交于,交于,若,则线段的长
A.大于9 B.等于9 C.小于9 D.不能确定
(
第
9
题图
) (
第
8
题图
)
9.如图所示的正方形网格中,网格线的交点称为格点.已知,是两个格点,如果点也是图形中的格点,且为等腰三角形,所有符合条件的点有
A.3个 B.4个 C.5个 D.6个
10.一艘轮船由海平面上地出发向南偏西的方向行驶100海里到达地,再由地向北偏西的方向行驶100海里到达地,则,两地相距
A.100海里 B.80海里 C.60海里 D.40海里
二.填空题(共8小题,每小题3分,共24分)
11.把命题“两个锐角互余”改写成“如果那么”的形式 ,它是一个 (填“真命题”或“假命题”
12.如果一个等腰三角形的两边长分别是3、8,那么它的周长是 .
13.如果一个等腰三角形的一角为,那么它的顶角是 .
14.如图,,分别是的高和角平分线,,,则
.
(
第
17
题图
) (
第
16
题图
) (
第
14
题图
)
15.中,,则是 三角形.
16.一副三角板如图放置,则的度数为 .
17.如图,是等边三角形内任意一点,过点作,,分别交,,于点,,,已知等边三角形的周长18,则 .
18.如图,在第1个△中,,,在边上任取一点,延长到,使,得到第2个△;在边上任取一点,延长到,使,得到第3个△按此做法继续下去,则第2022个三角形中,以为顶点的底角的度数是 .
三.解答题(共6小题,满分46分,其中19题6分,20—24每小题8分)
19.已知,,是一个三角形的三边长,
(1)填入“、或”号: 0, 0, 0.
(2)化简:.
20.如图,在中,,分别是,上的点,,是上的点,连接,,,已知,.
(1)求证:;
(2)若是的平分线,,求的度数.
21.如图,在中,,于.
(1)求证:;
(2)若平分分别交、于、,求证:是等腰三角形.
22.如图,在中,,点为上一点,且满足.点是的中点,连接并延长,交的延长线于点,连接.
(1)求和的度数;
(2)求证:是等腰三角形.
23.学习几何时,要善于对课本例习题中的典型图形进行变式研究.在中,,,是边上的高,点为直线上点,且.
(1)如图1,当点在边上时,求证:为等边三角形;
(2)如图2,当点在的延长线上时,求证:为等腰三角形.
24.数学课上,张老师举了下面的例题:
例1:等腰三角形中,,求的度数.(答案:
例2:等腰三角形中,,求的度数.(答案:或或
张老师启发同学们进行变式,小敏编的题目如下:
变式题:等腰三角形中,,求的度数.
(1)请你解答上面的变式题.
(2)请继续探索,完成下面问题:等腰三角形中,,则的度数为 .
(3)根据以上探索,我们发现,的度数不同,得到的度数的个数也可能不同.请你思考:当满足什么条件时,能得到三个不同的度数.
第2章《三角形2.1—2.3》培优试题2022-2023学年湘教版八年级数学上册参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 如果两个角是锐角,那么它们互余 , 假命题 .
12. 19 . 13. 或 . 14. 12 . 15. 直角 三角形.
16. . 17. 6 . 18. .
三.解答题(共6小题)
19.已知,,是一个三角形的三边长,
(1)填入“、或”号: 0, 0, 0.
(2)化简:.
【解】:(1),,是一个三角形的三边长,
,,,
(2)原式
.
20.如图,在中,,分别是,上的点,,是上的点,连接,,,已知,.
(1)求证:;
(2)若是的平分线,,求的度数.
【解】:(1)证明:,
.
,
.
;
(2)是的平分线,且,
,
,
,
.
21.如图,在中,,于.
(1)求证:;
(2)若平分分别交、于、,求证:是等腰三角形.
【证明】:(1),于,
,,
;
(2)在中,,
同理在中,.
又平分,
,
,
又,
,
,
是等腰三角形.
22.如图,在中,,点为上一点,且满足.点是的中点,连接并延长,交的延长线于点,连接.
(1)求和的度数;
(2)求证:是等腰三角形.
【解】:(1)设,
,
,
,
,
,
,
,
由可得,
解得:,
则,;
(2)是的中点,,
,即;
,
,
又,
,
又,
,
,
,即为等腰三角形.
23.学习几何时,要善于对课本例习题中的典型图形进行变式研究.在中,,,是边上的高,点为直线上点,且.
(1)如图1,当点在边上时,求证:为等边三角形;
(2)如图2,当点在的延长线上时,求证:为等腰三角形.
【证明】:(1),,
为等边三角形,,
是边上的高,
,
,
,
是等边三角形.
(2)同(1)可知,
,
为等边三角形,
,
,
,
即为等腰三角形.
24.数学课上,张老师举了下面的例题:
例1:等腰三角形中,,求的度数.(答案:
例2:等腰三角形中,,求的度数.(答案:或或
张老师启发同学们进行变式,小敏编的题目如下:
变式题:等腰三角形中,,求的度数.
(1)请你解答上面的变式题.
(2)请继续探索,完成下面问题:等腰三角形中,,则的度数为 .
(3)根据以上探索,我们发现,的度数不同,得到的度数的个数也可能不同.请你思考:当满足什么条件时,能得到三个不同的度数.
【解】:(1)当为顶角时,
;
当是顶角,则是底角,则;
当是顶角,则与都是底角,则,
综上所述,的度数为或或;
(2)因为有一个角为的等腰三角形为等边三角形,所以,
(3)分两种情况:设,
①当时,只能为顶角,
的度数只有一个;
②当时,
若为顶角,则;
若为底角,为顶角,则;
若为底角,为底角,则.
当且且,
即时,有三个不同的度数.
综上所述,可知当且时,有三个不同的度数.
一.选择题(共10小题,每小题3分,共30分)
1.如图,以为边的三角形的个数是
A.1个 B.2个 C.3个 D.4个
(
第
2
题图
)
(
第
1
题图
)
2.下列关于三角形的分类,有如图所示的甲、乙两种分法,则
A.甲、乙两种分法均正确 B.甲分法正确,乙分法错误
C.甲分法错误,乙分法正确 D.甲、乙两种分法均错误
3.下列各组图形中,是的高的图形是
A. B.
C. D.
4.下列长度的三条线段能组成三角形的是
A.3,4,8 B.5,6,11 C.5,6,10 D.4,4,9
5.如图,是的外角,,,,则的度数为
A. B. C. D.
(
第
6
题图
) (
第
5
题图
)
6.如图,在中,,,平分,则的度数
为
A. B. C. D.
7.下列命题是真命题的是
A.同位角相等
B.钝角三角形的两个锐角互余
C.若实数、满足,则
D.若实数、满足,,则
8.如图,在中,和的平分线交于点,过点作交于,交于,若,则线段的长
A.大于9 B.等于9 C.小于9 D.不能确定
(
第
9
题图
) (
第
8
题图
)
9.如图所示的正方形网格中,网格线的交点称为格点.已知,是两个格点,如果点也是图形中的格点,且为等腰三角形,所有符合条件的点有
A.3个 B.4个 C.5个 D.6个
10.一艘轮船由海平面上地出发向南偏西的方向行驶100海里到达地,再由地向北偏西的方向行驶100海里到达地,则,两地相距
A.100海里 B.80海里 C.60海里 D.40海里
二.填空题(共8小题,每小题3分,共24分)
11.把命题“两个锐角互余”改写成“如果那么”的形式 ,它是一个 (填“真命题”或“假命题”
12.如果一个等腰三角形的两边长分别是3、8,那么它的周长是 .
13.如果一个等腰三角形的一角为,那么它的顶角是 .
14.如图,,分别是的高和角平分线,,,则
.
(
第
17
题图
) (
第
16
题图
) (
第
14
题图
)
15.中,,则是 三角形.
16.一副三角板如图放置,则的度数为 .
17.如图,是等边三角形内任意一点,过点作,,分别交,,于点,,,已知等边三角形的周长18,则 .
18.如图,在第1个△中,,,在边上任取一点,延长到,使,得到第2个△;在边上任取一点,延长到,使,得到第3个△按此做法继续下去,则第2022个三角形中,以为顶点的底角的度数是 .
三.解答题(共6小题,满分46分,其中19题6分,20—24每小题8分)
19.已知,,是一个三角形的三边长,
(1)填入“、或”号: 0, 0, 0.
(2)化简:.
20.如图,在中,,分别是,上的点,,是上的点,连接,,,已知,.
(1)求证:;
(2)若是的平分线,,求的度数.
21.如图,在中,,于.
(1)求证:;
(2)若平分分别交、于、,求证:是等腰三角形.
22.如图,在中,,点为上一点,且满足.点是的中点,连接并延长,交的延长线于点,连接.
(1)求和的度数;
(2)求证:是等腰三角形.
23.学习几何时,要善于对课本例习题中的典型图形进行变式研究.在中,,,是边上的高,点为直线上点,且.
(1)如图1,当点在边上时,求证:为等边三角形;
(2)如图2,当点在的延长线上时,求证:为等腰三角形.
24.数学课上,张老师举了下面的例题:
例1:等腰三角形中,,求的度数.(答案:
例2:等腰三角形中,,求的度数.(答案:或或
张老师启发同学们进行变式,小敏编的题目如下:
变式题:等腰三角形中,,求的度数.
(1)请你解答上面的变式题.
(2)请继续探索,完成下面问题:等腰三角形中,,则的度数为 .
(3)根据以上探索,我们发现,的度数不同,得到的度数的个数也可能不同.请你思考:当满足什么条件时,能得到三个不同的度数.
第2章《三角形2.1—2.3》培优试题2022-2023学年湘教版八年级数学上册参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 如果两个角是锐角,那么它们互余 , 假命题 .
12. 19 . 13. 或 . 14. 12 . 15. 直角 三角形.
16. . 17. 6 . 18. .
三.解答题(共6小题)
19.已知,,是一个三角形的三边长,
(1)填入“、或”号: 0, 0, 0.
(2)化简:.
【解】:(1),,是一个三角形的三边长,
,,,
(2)原式
.
20.如图,在中,,分别是,上的点,,是上的点,连接,,,已知,.
(1)求证:;
(2)若是的平分线,,求的度数.
【解】:(1)证明:,
.
,
.
;
(2)是的平分线,且,
,
,
,
.
21.如图,在中,,于.
(1)求证:;
(2)若平分分别交、于、,求证:是等腰三角形.
【证明】:(1),于,
,,
;
(2)在中,,
同理在中,.
又平分,
,
,
又,
,
,
是等腰三角形.
22.如图,在中,,点为上一点,且满足.点是的中点,连接并延长,交的延长线于点,连接.
(1)求和的度数;
(2)求证:是等腰三角形.
【解】:(1)设,
,
,
,
,
,
,
,
由可得,
解得:,
则,;
(2)是的中点,,
,即;
,
,
又,
,
又,
,
,
,即为等腰三角形.
23.学习几何时,要善于对课本例习题中的典型图形进行变式研究.在中,,,是边上的高,点为直线上点,且.
(1)如图1,当点在边上时,求证:为等边三角形;
(2)如图2,当点在的延长线上时,求证:为等腰三角形.
【证明】:(1),,
为等边三角形,,
是边上的高,
,
,
,
是等边三角形.
(2)同(1)可知,
,
为等边三角形,
,
,
,
即为等腰三角形.
24.数学课上,张老师举了下面的例题:
例1:等腰三角形中,,求的度数.(答案:
例2:等腰三角形中,,求的度数.(答案:或或
张老师启发同学们进行变式,小敏编的题目如下:
变式题:等腰三角形中,,求的度数.
(1)请你解答上面的变式题.
(2)请继续探索,完成下面问题:等腰三角形中,,则的度数为 .
(3)根据以上探索,我们发现,的度数不同,得到的度数的个数也可能不同.请你思考:当满足什么条件时,能得到三个不同的度数.
【解】:(1)当为顶角时,
;
当是顶角,则是底角,则;
当是顶角,则与都是底角,则,
综上所述,的度数为或或;
(2)因为有一个角为的等腰三角形为等边三角形,所以,
(3)分两种情况:设,
①当时,只能为顶角,
的度数只有一个;
②当时,
若为顶角,则;
若为底角,为顶角,则;
若为底角,为底角,则.
当且且,
即时,有三个不同的度数.
综上所述,可知当且时,有三个不同的度数.
同课章节目录
