2022-2023学年沪科版九年级数学上册21.2.1 二次函数y=ax2图象性质 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年沪科版九年级数学上册21.2.1 二次函数y=ax2图象性质 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第21章 二次函数
21.2 二次函数图象性质
21.2.1 二次函数
学习目标
1
新课导入
2
新课讲解
3
课堂小结
4
当堂小练
5
拓展与延伸
7
布置作业
6
目录
学习目标
1
请替换文字内容
01
重点在于领悟二次函数渗透的
数学思想:数形结合
02
掌握二次函数的一般性质;
新课导入
2
一次函数的图象是一条_____ .
(2) 画函数的图象一般步骤是什么?
(3) 二次函数的图象是什么形状呢?
接下来我们就以为例,绘制
该二次函数图象,并说明情况。
直线
列表、描点、连线
结合图象讨论性质是
数形结合的研究函数
的重要方法.我们得
从最简单的二次函数
开始逐步深入地讨论
一般二次函数的图象
和性质.
新课导入
2
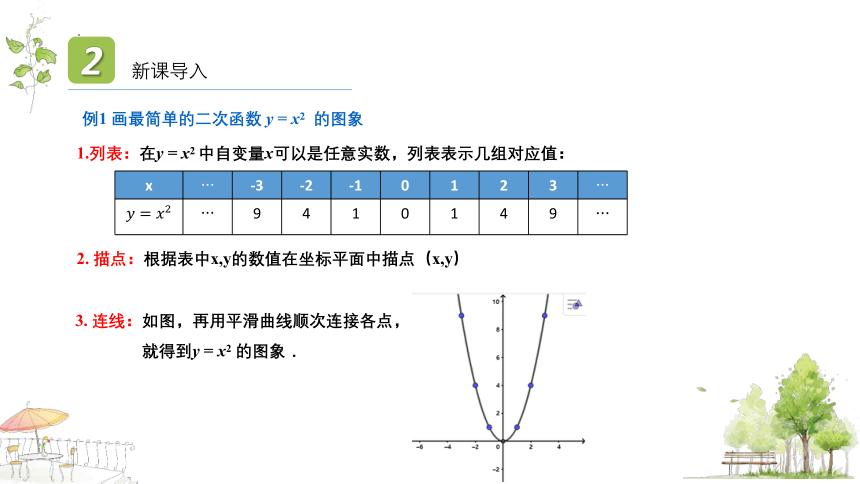
例1 画最简单的二次函数 y = x2 的图象
1.列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x -3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,
就得到y = x2 的图象.
新课讲解
3
x
y
O
-3
3
3
6
9
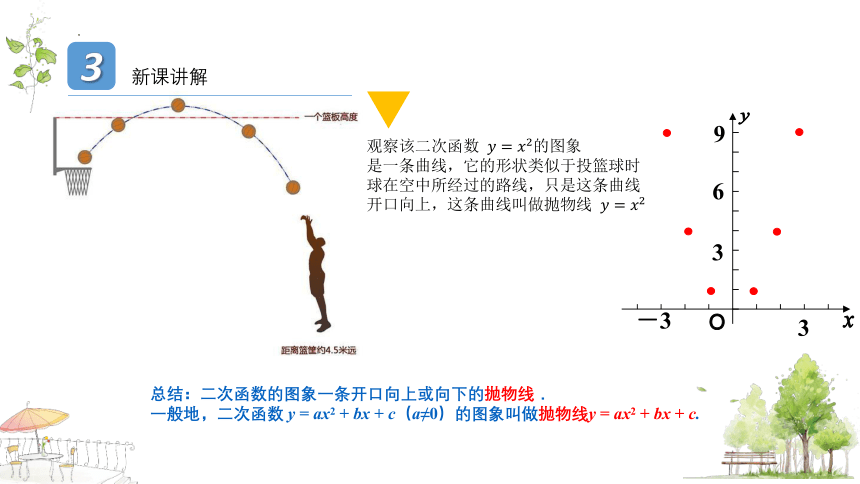
观察该二次函数 的图象
是一条曲线,它的形状类似于投篮球时
球在空中所经过的路线,只是这条曲线
开口向上,这条曲线叫做抛物线
总结:二次函数的图象一条开口向上或向下的抛物线.
一般地,二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c.
新课讲解
3
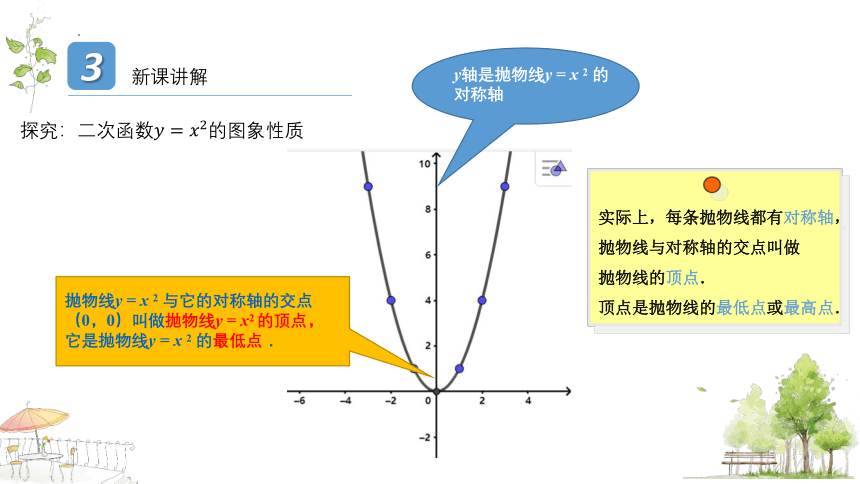
探究:二次函数图象性质
y轴是抛物线y = x 2 的
对称轴
抛物线y = x 2 与它的对称轴的交点(0,0)叫做抛物线y = x2 的顶点,
它是抛物线y = x 2 的最低点.
实际上,每条抛物线都有对称轴,
抛物线与对称轴的交点叫做
抛物线的顶点.
顶点是抛物线的最低点或最高点.
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
例2 在同一直角坐标系中,画出函数的图象.
··· -2 -1 0 1 2 ···
··· 2 0 2 ···
··· 8 2 0 2 8 ···
x
y
O
-2
2
2
4
6
4
-4
8
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
x
y
O
-2
2
2
4
6
4
-4
8
函数的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴.
相同点
相同点
不同点
a 的值越大,抛物线的开口程度越小.
那么当a<0时呢,试通过比较来说明情况
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
例3.请同学们画出函数
的图象,并考虑这些抛物线有什么共同点
和不同点.
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
大小对函数y=x2图象开口大小有什么影响?
思考
课堂小结
4
二次函数y=ax2的性质
抛物线 >0
顶点坐标
对称轴 轴或直线 轴直线
位置 位于x轴上方(除顶点外) 位于x轴下方(除顶点外)
开口方向 向上 向下
增减性 在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小
最值 当x=0时,函数最小值为0 当x=0时,函数最大值为0
以说明
|a|越大,抛物线开口程度越小,反之亦然
当堂小练
5
例1 抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在 侧,y随着x的增大而增大;
在 侧,y随着x的增大而减小,
当x= 时,函数y的值最小,最小值是 ,
抛物线y=2x2在x轴的 方(除顶点外).
例2 抛物线 在x轴的 方(除顶点外),
在对称轴的左侧,y随着x的 ;
在对称轴的右侧,y随着x的 ,
当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
(0,0)
Y轴
下
Y轴左侧
0
0
上
Y轴右侧
增大而增大
增大而减小
0
≠
法1:可以利用y=ax2 的性质直接解题,重点在于对函数模型的熟练掌握。
法2:二次函数在于考察数形结合的思想,同学们可以通过绘制图形来归纳总结
当堂小练
5
例1:在同一平面直角坐标系中,画出和的图象
例2:已知函数y=-不画图像,回答下列各题:
(1)其图象的开口方向:_____.
(2)其图象的对称轴:______.
(3)其图象的顶点坐标:______.
(4)当>0时,随的增大而_____.
当____时,函数的最___值是___
例3:如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数, ,则阴影部分面积为______.
利用对称性解题,地球人都知道!!
布置作业
6
1、课本P10页练习
2、同步学案21·2第1课时
3、预习第2课时
拓展与延伸
7
如图,在平面直角坐标系中,正方形的顶点的坐标分别为, , .若抛物线的图象与正方形有公共点,则的取值范围是_____.
本题主要考察大小对抛物线开口程度的影响
①当抛物线过点B时,抛物线开口程度最小,a取最大值;
②当抛物线过点D时,抛物线开口程度最大,a取最小值;
感谢观看
授课人:XXX 班级:312班
第21章 二次函数
21.2 二次函数图象性质
21.2.1 二次函数
学习目标
1
新课导入
2
新课讲解
3
课堂小结
4
当堂小练
5
拓展与延伸
7
布置作业
6
目录
学习目标
1
请替换文字内容
01
重点在于领悟二次函数渗透的
数学思想:数形结合
02
掌握二次函数的一般性质;
新课导入
2
一次函数的图象是一条_____ .
(2) 画函数的图象一般步骤是什么?
(3) 二次函数的图象是什么形状呢?
接下来我们就以为例,绘制
该二次函数图象,并说明情况。
直线
列表、描点、连线
结合图象讨论性质是
数形结合的研究函数
的重要方法.我们得
从最简单的二次函数
开始逐步深入地讨论
一般二次函数的图象
和性质.
新课导入
2
例1 画最简单的二次函数 y = x2 的图象
1.列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x -3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,
就得到y = x2 的图象.
新课讲解
3
x
y
O
-3
3
3
6
9
观察该二次函数 的图象
是一条曲线,它的形状类似于投篮球时
球在空中所经过的路线,只是这条曲线
开口向上,这条曲线叫做抛物线
总结:二次函数的图象一条开口向上或向下的抛物线.
一般地,二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c.
新课讲解
3
探究:二次函数图象性质
y轴是抛物线y = x 2 的
对称轴
抛物线y = x 2 与它的对称轴的交点(0,0)叫做抛物线y = x2 的顶点,
它是抛物线y = x 2 的最低点.
实际上,每条抛物线都有对称轴,
抛物线与对称轴的交点叫做
抛物线的顶点.
顶点是抛物线的最低点或最高点.
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
例2 在同一直角坐标系中,画出函数的图象.
··· -2 -1 0 1 2 ···
··· 2 0 2 ···
··· 8 2 0 2 8 ···
x
y
O
-2
2
2
4
6
4
-4
8
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
x
y
O
-2
2
2
4
6
4
-4
8
函数的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴.
相同点
相同点
不同点
a 的值越大,抛物线的开口程度越小.
那么当a<0时呢,试通过比较来说明情况
新课讲解
3
y轴是抛物线y = x 2 的
对称轴
例3.请同学们画出函数
的图象,并考虑这些抛物线有什么共同点
和不同点.
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
大小对函数y=x2图象开口大小有什么影响?
思考
课堂小结
4
二次函数y=ax2的性质
抛物线 >0
顶点坐标
对称轴 轴或直线 轴直线
位置 位于x轴上方(除顶点外) 位于x轴下方(除顶点外)
开口方向 向上 向下
增减性 在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小
最值 当x=0时,函数最小值为0 当x=0时,函数最大值为0
以说明
|a|越大,抛物线开口程度越小,反之亦然
当堂小练
5
例1 抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在 侧,y随着x的增大而增大;
在 侧,y随着x的增大而减小,
当x= 时,函数y的值最小,最小值是 ,
抛物线y=2x2在x轴的 方(除顶点外).
例2 抛物线 在x轴的 方(除顶点外),
在对称轴的左侧,y随着x的 ;
在对称轴的右侧,y随着x的 ,
当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
(0,0)
Y轴
下
Y轴左侧
0
0
上
Y轴右侧
增大而增大
增大而减小
0
≠
法1:可以利用y=ax2 的性质直接解题,重点在于对函数模型的熟练掌握。
法2:二次函数在于考察数形结合的思想,同学们可以通过绘制图形来归纳总结
当堂小练
5
例1:在同一平面直角坐标系中,画出和的图象
例2:已知函数y=-不画图像,回答下列各题:
(1)其图象的开口方向:_____.
(2)其图象的对称轴:______.
(3)其图象的顶点坐标:______.
(4)当>0时,随的增大而_____.
当____时,函数的最___值是___
例3:如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数, ,则阴影部分面积为______.
利用对称性解题,地球人都知道!!
布置作业
6
1、课本P10页练习
2、同步学案21·2第1课时
3、预习第2课时
拓展与延伸
7
如图,在平面直角坐标系中,正方形的顶点的坐标分别为, , .若抛物线的图象与正方形有公共点,则的取值范围是_____.
本题主要考察大小对抛物线开口程度的影响
①当抛物线过点B时,抛物线开口程度最小,a取最大值;
②当抛物线过点D时,抛物线开口程度最大,a取最小值;
感谢观看
授课人:XXX 班级:312班
