沪科版九年级21.2 二次函数的图象和性质同步学案(含答案)
文档属性
| 名称 | 沪科版九年级21.2 二次函数的图象和性质同步学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 403.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
二次函数与反比例函数
21.2 二次函数的图像性质
二次函数的图象性质:
一次函数的图象是一条直线,那么二次函数的图象是什么形状呢?
例1:绘制二次函数的图象.
列表
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
二、描点:
三、连线
总结:通过图象不难发现,函数是一条关于_y轴__对称的曲线,我们可以把这条曲线叫做__双曲线____.
该抛物线的开口_向上___.
__y轴____或__x=0____是它的对称轴.
对称轴与抛物线的交点就是该抛物线的_顶点______.
抛物线的顶点也是该图像的最__低__点.
当_x<0____时,随着的增大而_减小___.
当_x>0____时,随着的增大而_增大___
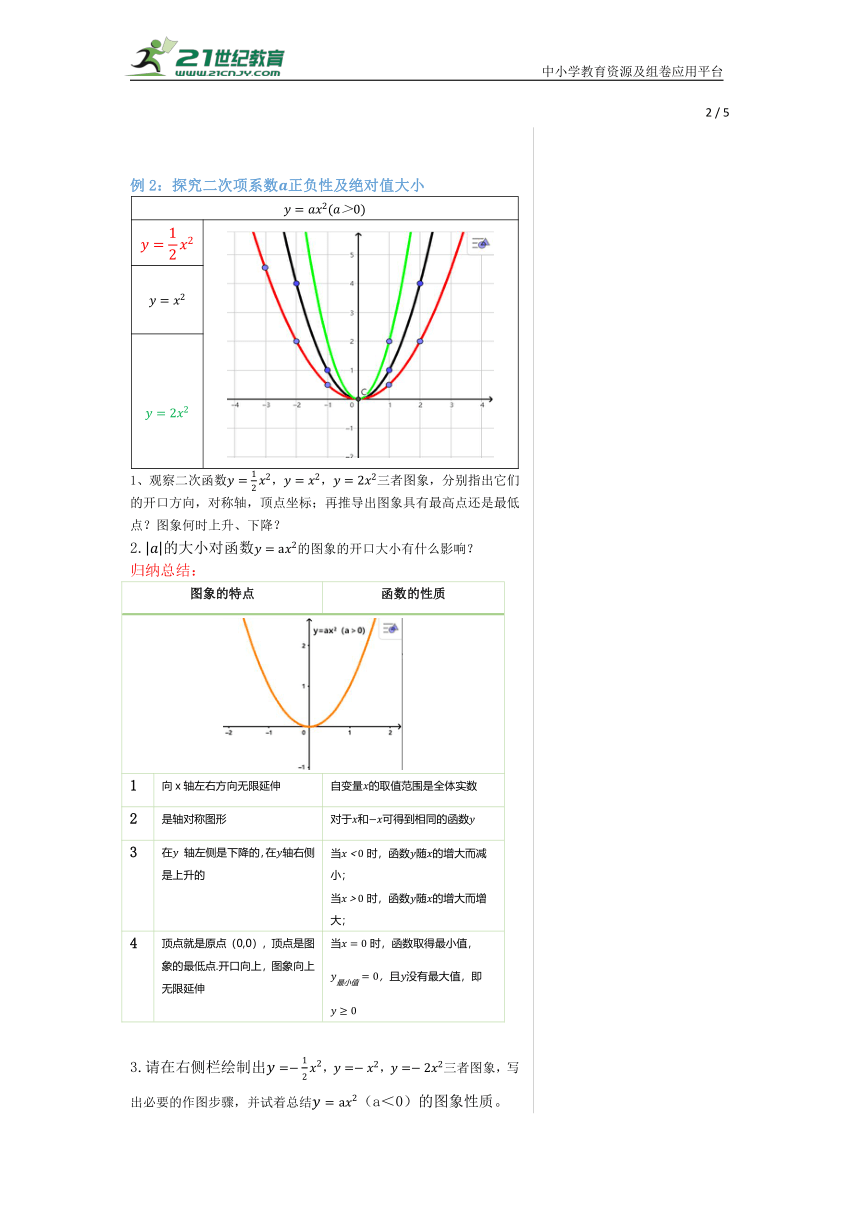
例2:探究二次项系数正负性及绝对值大小
1、观察二次函数,,三者图象,分别指出它们的开口方向,对称轴,顶点坐标;再推导出图象具有最高点还是最低点?图象何时上升、下降?
2.的大小对函数的图象的开口大小有什么影响?
归纳总结:
图象的特点 函数的性质
1 向x轴左右方向无限延伸 自变量的取值范围是全体实数
2 是轴对称图形 对于和可得到相同的函数
3 在 轴左侧是下降的,在轴右侧是上升的 当时,函数随的增大而减小; 当时,函数随的增大而增大;
4 顶点就是原点(0,0),顶点是图象的最低点.开口向上,图象向上无限延伸 当时,函数取得最小值,且没有最大值,即
3.请在右侧栏绘制出,,三者图象,写出必要的作图步骤,并试着总结(a<0)的图象性质。
图象的特点 函数的性质
1 向x轴左右方向无限延伸 自变量的取值范围是__全体实数____.
2 是___轴对称_____图形 对于和可得到相同的函数
3 在 轴左侧是_上升的_____,在轴右侧是__下降的____. 当时,函数随的增大而_增大_____; 当时,函数随的增大而__减小____;
4 顶点就是原点(0,0),顶点是图象的__最高点_____,开口__向下_____,图象向_下__无限延伸 当时,函数取得最_大__值,且没有最_小__值,即
例 1若点在二次函数的图象上,则下列坐标表示的点也在该抛物线图象上的是( ).
B. C. D.
例2. 若抛物线的对称轴左侧,随的增大而增大,则的值为( )
B.- C. ± D.
例3.已知函数不画图像,回答下列各题:
其图象的开口方向:_向下____.
其图象的对称轴:_y轴_____.
其图象的顶点坐标:_(0,0)__.
当时,随的增大而_减小____.
当_=0___时,函数的最_大__值是_0__.
例4.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数,,则阴影部分面积为__8____.
例5. 点平行于轴的直线分别交抛物线与于两点,过点作轴的平行线交于点直线,交于点,则的长为__2___.
在平面直角坐标系中,已知点,点 如果二次函数图象与线段PQ有交点,那么的取值范围为
≤a≤2.
例7. 已知抛物线经过三点,则的大小关系是_<<_____;(用“<”连接 )
例8.如图,在平面直角坐标系中,正方形的顶点的坐标分别为.若抛物线的图象与正方形有公共点,则的取值范围是_≤a≤3____.
在同一平面直角坐标系中,画出和的图象,
答案:略
例10. 二次函数的图象与直线交于点.
求的值
写出二次函数的解析式,并指出取何值时,随
的增大而增大?
写出二次函数的顶点坐标和对称轴
答案:
点P在的图像上,
∴=2×1-1=1代入解得=1
二次函数的表达式:
因为函数的开口向上,对称轴为y轴,当>0时,y随x的增大而增大。
二次函数与反比例函数
21.2 二次函数的图像性质
二次函数的图象性质:
一次函数的图象是一条直线,那么二次函数的图象是什么形状呢?
例1:绘制二次函数的图象.
列表
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
二、描点:
三、连线
总结:通过图象不难发现,函数是一条关于_y轴__对称的曲线,我们可以把这条曲线叫做__双曲线____.
该抛物线的开口_向上___.
__y轴____或__x=0____是它的对称轴.
对称轴与抛物线的交点就是该抛物线的_顶点______.
抛物线的顶点也是该图像的最__低__点.
当_x<0____时,随着的增大而_减小___.
当_x>0____时,随着的增大而_增大___
例2:探究二次项系数正负性及绝对值大小
1、观察二次函数,,三者图象,分别指出它们的开口方向,对称轴,顶点坐标;再推导出图象具有最高点还是最低点?图象何时上升、下降?
2.的大小对函数的图象的开口大小有什么影响?
归纳总结:
图象的特点 函数的性质
1 向x轴左右方向无限延伸 自变量的取值范围是全体实数
2 是轴对称图形 对于和可得到相同的函数
3 在 轴左侧是下降的,在轴右侧是上升的 当时,函数随的增大而减小; 当时,函数随的增大而增大;
4 顶点就是原点(0,0),顶点是图象的最低点.开口向上,图象向上无限延伸 当时,函数取得最小值,且没有最大值,即
3.请在右侧栏绘制出,,三者图象,写出必要的作图步骤,并试着总结(a<0)的图象性质。
图象的特点 函数的性质
1 向x轴左右方向无限延伸 自变量的取值范围是__全体实数____.
2 是___轴对称_____图形 对于和可得到相同的函数
3 在 轴左侧是_上升的_____,在轴右侧是__下降的____. 当时,函数随的增大而_增大_____; 当时,函数随的增大而__减小____;
4 顶点就是原点(0,0),顶点是图象的__最高点_____,开口__向下_____,图象向_下__无限延伸 当时,函数取得最_大__值,且没有最_小__值,即
例 1若点在二次函数的图象上,则下列坐标表示的点也在该抛物线图象上的是( ).
B. C. D.
例2. 若抛物线的对称轴左侧,随的增大而增大,则的值为( )
B.- C. ± D.
例3.已知函数不画图像,回答下列各题:
其图象的开口方向:_向下____.
其图象的对称轴:_y轴_____.
其图象的顶点坐标:_(0,0)__.
当时,随的增大而_减小____.
当_=0___时,函数的最_大__值是_0__.
例4.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数,,则阴影部分面积为__8____.
例5. 点平行于轴的直线分别交抛物线与于两点,过点作轴的平行线交于点直线,交于点,则的长为__2___.
在平面直角坐标系中,已知点,点 如果二次函数图象与线段PQ有交点,那么的取值范围为
≤a≤2.
例7. 已知抛物线经过三点,则的大小关系是_<<_____;(用“<”连接 )
例8.如图,在平面直角坐标系中,正方形的顶点的坐标分别为.若抛物线的图象与正方形有公共点,则的取值范围是_≤a≤3____.
在同一平面直角坐标系中,画出和的图象,
答案:略
例10. 二次函数的图象与直线交于点.
求的值
写出二次函数的解析式,并指出取何值时,随
的增大而增大?
写出二次函数的顶点坐标和对称轴
答案:
点P在的图像上,
∴=2×1-1=1代入解得=1
二次函数的表达式:
因为函数的开口向上,对称轴为y轴,当>0时,y随x的增大而增大。
