人教版数学八年级上册 第十一章专题四 模型拓展——三角形的角平分线模型 课件(共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十一章专题四 模型拓展——三角形的角平分线模型 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 555.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:03:55 | ||
图片预览






文档简介
(共14张PPT)
第十一章 三角形
专题四 模型拓展——
三角形的角平分线模型
目录
01
模型解读
02
针对训练
类型一:双内角平分线模型
模型解读
针对训练
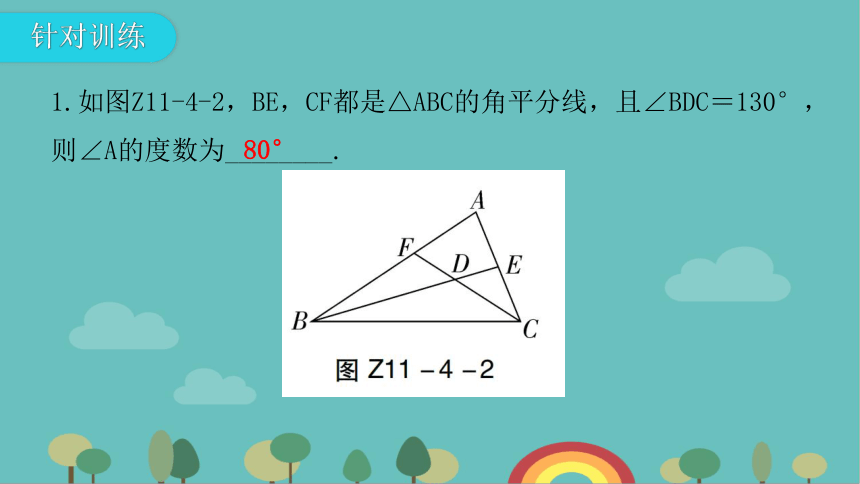
1.如图Z11-4-2,BE,CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为________.
80°
模型解读
类型二:双外角平分线模型
针对训练
2.如图Z11-4-4,在△ABC中,BD,CD分别是∠ABC和∠ACB的平分线,BP,CP分别是∠EBC和∠FCB的平分线.
(1)若∠A=30°,则∠BDC的度数为________,
∠BPC的度数为________;
(2)当∠A变化时,∠D+∠P的值是否变化?请说
明理由.
105°
75°
模型解读
类型三:内外角平分线模型
针对训练
3.(苏教七下P43改编)如图Z11-4-6,∠MON=90°,点A,B分别在OM,ON上运动,BE是∠ABN的平分线,BE的反向延长线交∠OAB的平分线于点C.试问∠C的大小是否会随点A,B的运动而发生变化?如果不会,求出∠C的度数;如果会,请求出变化范围.
模型解读
类型四:对顶角三角形内角平分线的夹角模型
针对训练
4.如图Z11-4-8①,已知线段AB,CD相交于点O,连接AC,BD,我们把形如这样的图形称为“8字型”.如图Z11-4-8②,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD,AB分别相交于点M,N.
(1)以线段AC为边的“8字型”有______个,以点O为交点的“8字型”有______个;
(2)若∠B=100°,∠C=
120°,求∠P的度数.
3
4
谢 谢
第十一章 三角形
专题四 模型拓展——
三角形的角平分线模型
目录
01
模型解读
02
针对训练
类型一:双内角平分线模型
模型解读
针对训练
1.如图Z11-4-2,BE,CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为________.
80°
模型解读
类型二:双外角平分线模型
针对训练
2.如图Z11-4-4,在△ABC中,BD,CD分别是∠ABC和∠ACB的平分线,BP,CP分别是∠EBC和∠FCB的平分线.
(1)若∠A=30°,则∠BDC的度数为________,
∠BPC的度数为________;
(2)当∠A变化时,∠D+∠P的值是否变化?请说
明理由.
105°
75°
模型解读
类型三:内外角平分线模型
针对训练
3.(苏教七下P43改编)如图Z11-4-6,∠MON=90°,点A,B分别在OM,ON上运动,BE是∠ABN的平分线,BE的反向延长线交∠OAB的平分线于点C.试问∠C的大小是否会随点A,B的运动而发生变化?如果不会,求出∠C的度数;如果会,请求出变化范围.
模型解读
类型四:对顶角三角形内角平分线的夹角模型
针对训练
4.如图Z11-4-8①,已知线段AB,CD相交于点O,连接AC,BD,我们把形如这样的图形称为“8字型”.如图Z11-4-8②,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD,AB分别相交于点M,N.
(1)以线段AC为边的“8字型”有______个,以点O为交点的“8字型”有______个;
(2)若∠B=100°,∠C=
120°,求∠P的度数.
3
4
谢 谢
