人教版数学八年级上册13.1.2 线段的垂直平分线的性质(一) 导练课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2 线段的垂直平分线的性质(一) 导练课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 369.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:08:30 | ||
图片预览




文档简介
(共17张PPT)
第十三章 轴对称
第19课时 线段的垂直平分线的性质(一)
目录
01
本课目标
02
课堂导练
1.理解线段的垂直平分线的定义.
2.掌握线段的垂直平分线的性质和判定.
3.能运用线段垂直平分线的性质和判定解决实际问题.
本课目标
知识重点
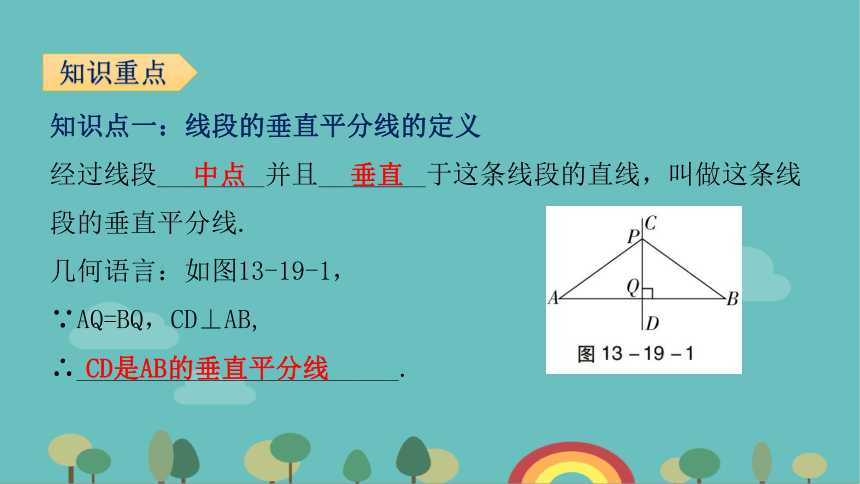
知识点一:线段的垂直平分线的定义
经过线段________并且________于这条线段的直线,叫做这条线段的垂直平分线.
几何语言:如图13-19-1,
∵AQ=BQ,CD⊥AB,
∴________________________.
中点
垂直
CD是AB的垂直平分线
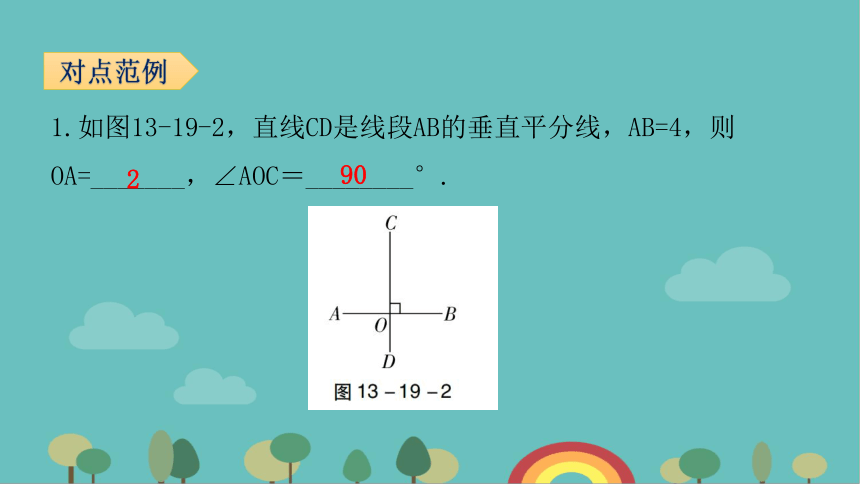
1.如图13-19-2,直线CD是线段AB的垂直平分线,AB=4,则OA=_______,∠AOC=________°.
对点范例
2
90
知识点二:线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离________.
几何语言:如图13-19-3,
∵CD是AB的垂直平分线,P是CD上一点,
∴________.
知识重点
相等
PA=PB
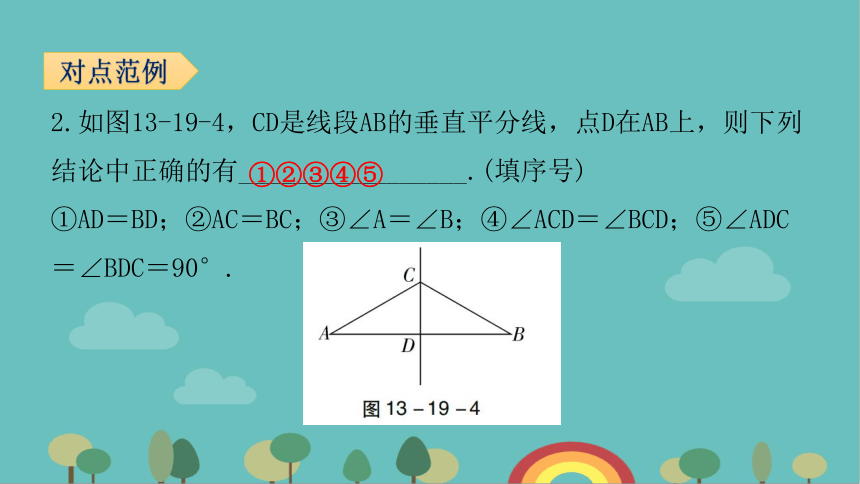
2.如图13-19-4,CD是线段AB的垂直平分线,点D在AB上,则下列结论中正确的有_________________.(填序号)
①AD=BD;②AC=BC;③∠A=∠B;④∠ACD=∠BCD;⑤∠ADC=∠BDC=90°.
对点范例
①②③④⑤
知识点三:线段的垂直平分线的判定
与一条线段两个端点距离相等的点,在______________________.
几何语言:如图13-19-5,
∵________,
∴点P在AB的垂直平分线上.
知识重点
这条线段的垂直平分线上
PA=PB
3.如图13-19-6,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( )
A.PO⊥AB
B.AO=BO
C.PO是线段AB的垂直平分线
D.P在线段AB的垂直平分线上
对点范例
D
课堂导练
【例1】(北师八下P24改编)如图13-19-7,在△ABC中,DE是AC的垂直平分线,△ABC的周长为21 cm,△ABD的周长为13 cm,求AE的长.
典型例题
思路点拨:根据线段垂直平分线上任意一点与这条线段两个端点的距离相等计算即可.
1.(人教八上P65改编、北师八下P23改编)如图13-19-8,在△ABC中,DE是AC的垂直平分线,AE=3,△ABC的周长为14,求△BCD的周长.
举一反三
解:∵DE是AC的垂直平分线,AE=3,
∴AD=CD,AC=2AE=6.
∵△ABC的周长为14,
∴AB+BC=14-AC=8.
∴△BCD的周长为BD+CD+BC=AB+BC=8.
【例2】如图13-19-9,AC=AD,BC=BD,则下列判断正确的是( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
思路点拨:熟练掌握线段垂直平分线的判定是解题的关键.
典型例题
A
2.如图13-19-10,下列说法正确的是( )
A.若AC=BC,则CD是线段的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
举一反三
D
【例3】(人教八上P93改编)如图13-19-11,DE⊥AB,DF⊥AC,垂足分别为点E,F,DE=DF.求证:AD垂直平分EF.
思路点拨:根据线段的垂直平分线的判定来证明即可.
典型例题
3.(创新题)如图13-19-12,AD与BC相交于点O,OA=OC,∠A=∠C,EB=ED.求证:OE垂直平分BD.
举一反三
谢 谢
第十三章 轴对称
第19课时 线段的垂直平分线的性质(一)
目录
01
本课目标
02
课堂导练
1.理解线段的垂直平分线的定义.
2.掌握线段的垂直平分线的性质和判定.
3.能运用线段垂直平分线的性质和判定解决实际问题.
本课目标
知识重点
知识点一:线段的垂直平分线的定义
经过线段________并且________于这条线段的直线,叫做这条线段的垂直平分线.
几何语言:如图13-19-1,
∵AQ=BQ,CD⊥AB,
∴________________________.
中点
垂直
CD是AB的垂直平分线
1.如图13-19-2,直线CD是线段AB的垂直平分线,AB=4,则OA=_______,∠AOC=________°.
对点范例
2
90
知识点二:线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离________.
几何语言:如图13-19-3,
∵CD是AB的垂直平分线,P是CD上一点,
∴________.
知识重点
相等
PA=PB
2.如图13-19-4,CD是线段AB的垂直平分线,点D在AB上,则下列结论中正确的有_________________.(填序号)
①AD=BD;②AC=BC;③∠A=∠B;④∠ACD=∠BCD;⑤∠ADC=∠BDC=90°.
对点范例
①②③④⑤
知识点三:线段的垂直平分线的判定
与一条线段两个端点距离相等的点,在______________________.
几何语言:如图13-19-5,
∵________,
∴点P在AB的垂直平分线上.
知识重点
这条线段的垂直平分线上
PA=PB
3.如图13-19-6,直线PO与AB交于点O,且PA=PB,则下列结论中正确的是( )
A.PO⊥AB
B.AO=BO
C.PO是线段AB的垂直平分线
D.P在线段AB的垂直平分线上
对点范例
D
课堂导练
【例1】(北师八下P24改编)如图13-19-7,在△ABC中,DE是AC的垂直平分线,△ABC的周长为21 cm,△ABD的周长为13 cm,求AE的长.
典型例题
思路点拨:根据线段垂直平分线上任意一点与这条线段两个端点的距离相等计算即可.
1.(人教八上P65改编、北师八下P23改编)如图13-19-8,在△ABC中,DE是AC的垂直平分线,AE=3,△ABC的周长为14,求△BCD的周长.
举一反三
解:∵DE是AC的垂直平分线,AE=3,
∴AD=CD,AC=2AE=6.
∵△ABC的周长为14,
∴AB+BC=14-AC=8.
∴△BCD的周长为BD+CD+BC=AB+BC=8.
【例2】如图13-19-9,AC=AD,BC=BD,则下列判断正确的是( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
思路点拨:熟练掌握线段垂直平分线的判定是解题的关键.
典型例题
A
2.如图13-19-10,下列说法正确的是( )
A.若AC=BC,则CD是线段的垂直平分线
B.若AD=DB,则AC=BC
C.若CD⊥AB,则AC=BC
D.若CD是线段AB的垂直平分线,则AC=BC
举一反三
D
【例3】(人教八上P93改编)如图13-19-11,DE⊥AB,DF⊥AC,垂足分别为点E,F,DE=DF.求证:AD垂直平分EF.
思路点拨:根据线段的垂直平分线的判定来证明即可.
典型例题
3.(创新题)如图13-19-12,AD与BC相交于点O,OA=OC,∠A=∠C,EB=ED.求证:OE垂直平分BD.
举一反三
谢 谢
