2021—2022学年人教版数学八年级下册17.1.1 勾股定理 课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册17.1.1 勾股定理 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 618.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:36:42 | ||
图片预览



文档简介
(共18张PPT)
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。相传有一次他在
朋友家做客时,发现朋友家用砖
铺成的地面中反映了A、B、C三
者面积之间的数量关系,进而发
现直角三角形三边的某种数量关
系.
A
B
C
每块砖都是等腰直角三角形哦
问题1 三个正方形A,B,C 的面积有什么关系?
SA+SB=SC
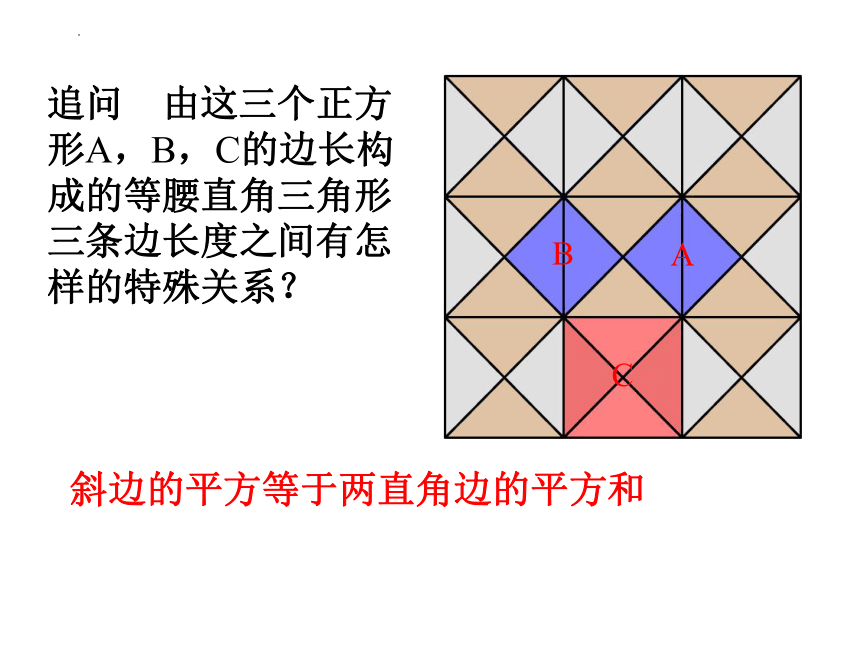
追问 由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?
A
B
C
斜边的平方等于两直角边的平方和
17.1.1 勾股定理
学习目标(1分钟)
(1)了解勾股定理的来源,并熟记它的字母表达。
(2)掌握勾股定理的证明方法,并会运用它求解直角三角形的边长。
自学指导一 (5分钟)
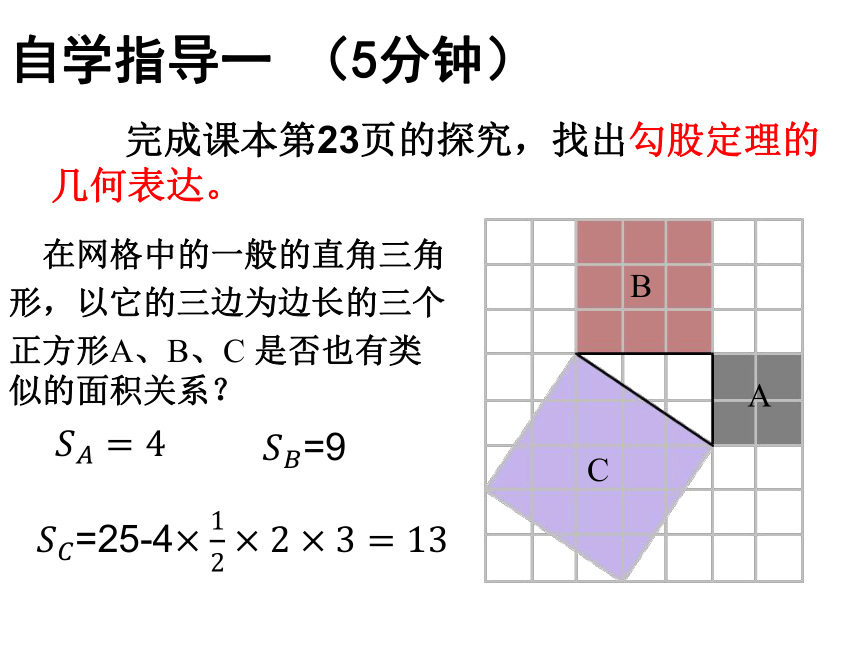
在网格中的一般的直角三角
形,以它的三边为边长的三个
正方形A、B、C 是否也有类似的面积关系?
完成课本第23页的探究,找出勾股定理的
几何表达。
A
B
C
=9
=25-4
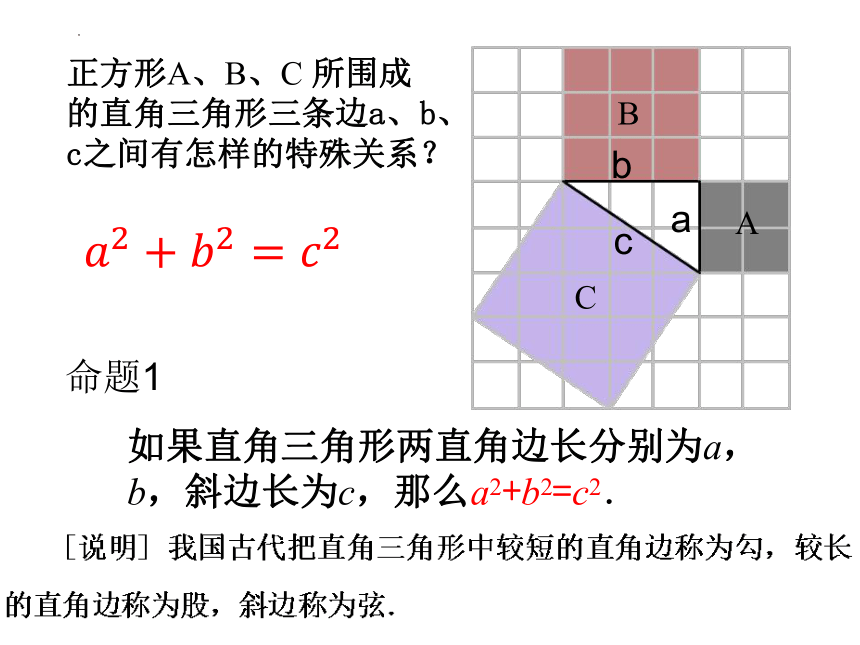
正方形A、B、C 所围成的直角三角形三条边a、b、c之间有怎样的特殊关系?
A
B
C
a
b
c
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
命题1
自学检测一(5分钟)
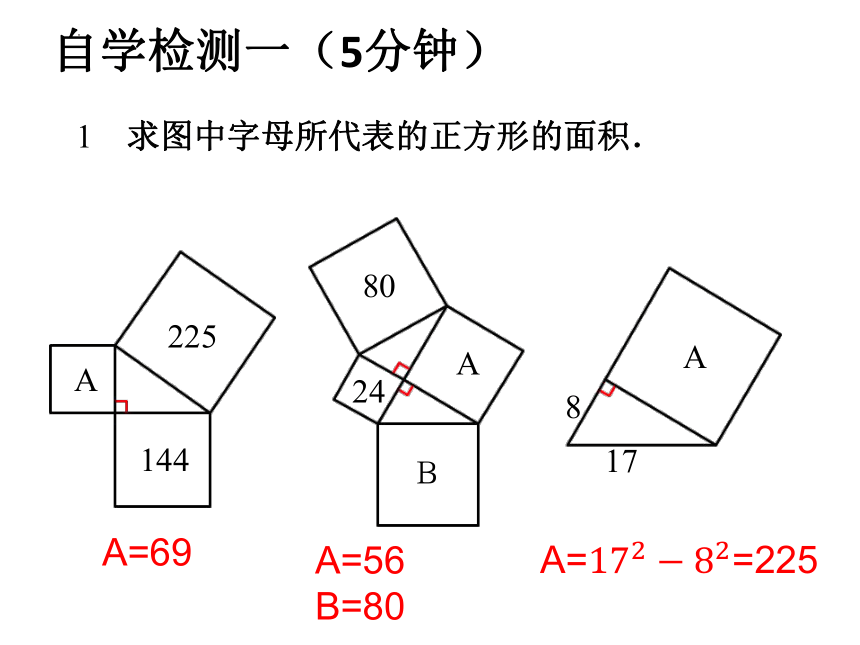
1 求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
A=69
A=56
B=80
A==225
2 求下列直角三角形中未知边的长度.
A
B
C
4
6
x
C
B
A
5
10
x
点拨运用(2分钟)
两边
A
B
C
b
a
c
a=4,b=3,求c=?
a=12,c=13,求b=?
5
5
自学指导二 (7分钟)
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究。
c
b
a
(
b
-
a
)
2
黄实
朱实
勾股定理的证明1:
命题1:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图(左)连在一起,通过剪、拼把它拼成图(右)的样子。你能做到吗?试试看。
c
b
a
b
a
讲授新课
通过图形的切割、拼接证明勾股定理
自学检测二(5分钟)
如图,通过面积的关系求证:
。
由“大正方形的面积=小正方形的面积+4个直角三角形的面积”,得
(a+b)2=c2+4×ab,即a2+b2=c2.
课堂小结 (1分钟)
今天掌握了什么知识?
1.勾股定理的表达形式:
2.通过面积的等量关系求证勾股定理。
当堂训练 (10分钟)
1 如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
解:由题意可得,
=+=400
=+=225
所以S正方形E=625
F
G
2 如图,邮票图案的三个正方形小方格中间是一个直角三角形,如果1个小方格为1个单位面积,那么直角三角形的两直角边长分别是____和____,斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
3、如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )
A.8 B.10
C.12 D.16
C
解析:∵AD⊥CD,CD=4,AD=3,
选做题
a
a
b
b
c
c
在1876年一个傍晚,伽菲尔德正在外面散步,他突然发现有两个小孩正在讨论着,其中一个小男孩正用树枝在地上画着一个直角三角形。于是伽菲尔德便问他们在干什么?那个小男孩说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答到:“那斜边的平方一定等于5的平方加上7的平方。”
小男孩又说道:“先生,你能说出
其中的道理吗?”伽菲尔德一时语塞,
无法解释了,心里很不是滋味。
由“梯形面积等于三个直角三角形面积之和”,得
a
a
b
b
c
c
解:
7.2 用坐标方法的简单应用
板书设计
1.勾股定理的表达形式:
2.通过面积的等量关系求证勾股定理。
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。相传有一次他在
朋友家做客时,发现朋友家用砖
铺成的地面中反映了A、B、C三
者面积之间的数量关系,进而发
现直角三角形三边的某种数量关
系.
A
B
C
每块砖都是等腰直角三角形哦
问题1 三个正方形A,B,C 的面积有什么关系?
SA+SB=SC
追问 由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?
A
B
C
斜边的平方等于两直角边的平方和
17.1.1 勾股定理
学习目标(1分钟)
(1)了解勾股定理的来源,并熟记它的字母表达。
(2)掌握勾股定理的证明方法,并会运用它求解直角三角形的边长。
自学指导一 (5分钟)
在网格中的一般的直角三角
形,以它的三边为边长的三个
正方形A、B、C 是否也有类似的面积关系?
完成课本第23页的探究,找出勾股定理的
几何表达。
A
B
C
=9
=25-4
正方形A、B、C 所围成的直角三角形三条边a、b、c之间有怎样的特殊关系?
A
B
C
a
b
c
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
命题1
自学检测一(5分钟)
1 求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
A=69
A=56
B=80
A==225
2 求下列直角三角形中未知边的长度.
A
B
C
4
6
x
C
B
A
5
10
x
点拨运用(2分钟)
两边
A
B
C
b
a
c
a=4,b=3,求c=?
a=12,c=13,求b=?
5
5
自学指导二 (7分钟)
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究。
c
b
a
(
b
-
a
)
2
黄实
朱实
勾股定理的证明1:
命题1:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图(左)连在一起,通过剪、拼把它拼成图(右)的样子。你能做到吗?试试看。
c
b
a
b
a
讲授新课
通过图形的切割、拼接证明勾股定理
自学检测二(5分钟)
如图,通过面积的关系求证:
。
由“大正方形的面积=小正方形的面积+4个直角三角形的面积”,得
(a+b)2=c2+4×ab,即a2+b2=c2.
课堂小结 (1分钟)
今天掌握了什么知识?
1.勾股定理的表达形式:
2.通过面积的等量关系求证勾股定理。
当堂训练 (10分钟)
1 如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
解:由题意可得,
=+=400
=+=225
所以S正方形E=625
F
G
2 如图,邮票图案的三个正方形小方格中间是一个直角三角形,如果1个小方格为1个单位面积,那么直角三角形的两直角边长分别是____和____,斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
3、如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )
A.8 B.10
C.12 D.16
C
解析:∵AD⊥CD,CD=4,AD=3,
选做题
a
a
b
b
c
c
在1876年一个傍晚,伽菲尔德正在外面散步,他突然发现有两个小孩正在讨论着,其中一个小男孩正用树枝在地上画着一个直角三角形。于是伽菲尔德便问他们在干什么?那个小男孩说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答到:“那斜边的平方一定等于5的平方加上7的平方。”
小男孩又说道:“先生,你能说出
其中的道理吗?”伽菲尔德一时语塞,
无法解释了,心里很不是滋味。
由“梯形面积等于三个直角三角形面积之和”,得
a
a
b
b
c
c
解:
7.2 用坐标方法的简单应用
板书设计
1.勾股定理的表达形式:
2.通过面积的等量关系求证勾股定理。
