2021—2022学年人教版数学八年级下册17.1.2勾股定理的应用 课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册17.1.2勾股定理的应用 课件(共17张PPT) | 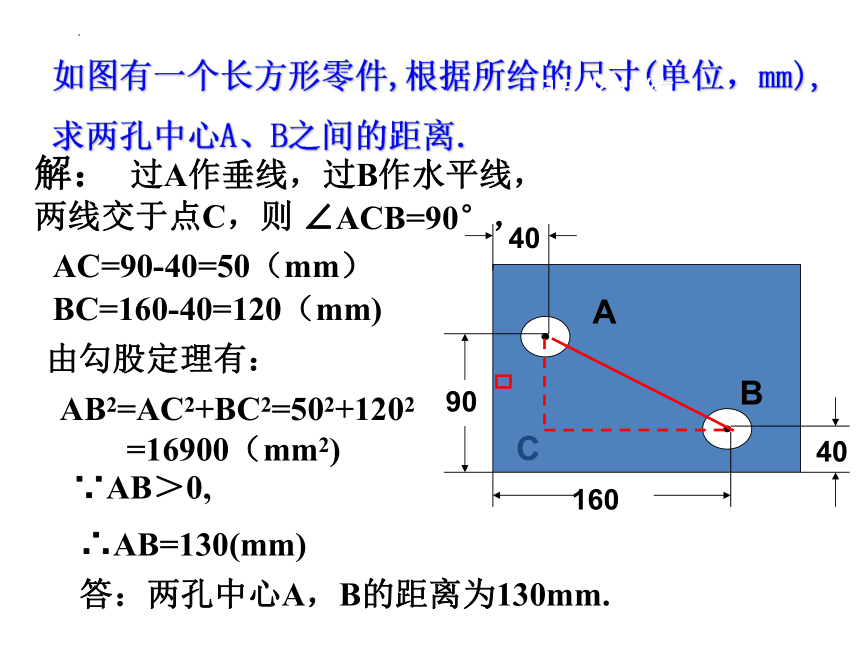 | |
| 格式 | zip | ||
| 文件大小 | 497.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:37:34 | ||
图片预览







文档简介
(共17张PPT)
如图有一个长方形零件,根据所给的尺寸(单位,mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解: 过A作垂线,过B作水平线,
两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
强化训练
17.1.2 勾股定理的应用
学习目标(1分钟)
(1)运用勾股定理求线段长度,并从实际问题中建立直角三角形的模型,解决一些简单的实际问题。
自学指导一 (5分钟)
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
提示:
A
B
C
D
1 m
2 m
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.
自学检测一(5分钟)
1.有一个小朋友拿着一根竹竿要通过一个长方
形的门,如果把竹竿竖放就比门高出一尺,斜
放就恰好等于门的对角线,已知门宽四尺,求
竹竿高与门高。
A
B
C
D
4尺
x 尺
解:设门高为x尺,则竹竿长
为(x+1)尺,
根据勾股定理可得x2+42=(x+1)2,
解得 x=7.5
故门高7.5尺,
竹竿高=7.5+1=8.5(尺)
自学指导二 (5分钟)
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?
(提示: )
解:(1)在Rt△AOB中,
根据勾股定理,
OB2=AB2-AO2=2.62-2.42=1
∴OB=1
(2)由题意可得,AC=0.5,OC=2.4-0.5=1.9
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-1.92=3.15
∴OD=
∴BD=OD-OB≈0.77
所以梯子的顶端沿墙下滑0.5m时,梯子底端
并不是也外移0.5m,而是外移约0.77m。
自学检测二(5分钟)
[解析] 设CD=x米,在Rt△ABC中,
可利用勾股定理建立等量关系,
列方程,并解方程求解.
探究问题三 求立体图形中表面上两点之间的最短距离
[解析] 沿长方体表面从点A爬到点B,
考虑路线最短的问题有三种途径:
(1)从右侧面和前面走.
(2)从右侧面和上底面走.
(3)从后侧面和上底面走,
由两点之间线段最短来确定路径.
例4 如图17-1-5所示,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,求这只蚂蚁要爬行的最短距离.
①
②
③
课堂小结 (3分钟)
(1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什么
好的突破办法?利用勾股定理解决实际问题的
注意点是什么?
(3)本节课体现出哪些数学思想方法,都在什么情
况下运用?
当堂训练 (10分钟)
(提示: )
选做题
2.如图所示,公路MN和公路PQ在P点处交会,点A处有一所中学,AP=160 m,点A到公路MN的距离为80 m.假设拖拉机行驶时,周围100 m以内会受到噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响 请说明理由;如果受影响,已知拖拉机的速度为18 km/h,那么学校受影响的时间为多少秒
分析:要判断拖拉机的噪音是否影响学校A,
实质上是看A到公路的距离是否小于100 m;
要求出学校受影响的时间,必须找到拖拉机
行至哪一点开始影响学校,行至哪一点后结束影响学校.
解:学校A到公路MN的距离为80 m,而拖拉机的噪声范围为100 m以内,80<100,故拖拉机会影响学校.如图所示,AB⊥MN,设C,D为公路MN上的两点,且AC=AD=100 m,则拖拉机行驶在CD段时,学校会受到噪声影响.
由题意,得AB=80,AC=100.
由勾股定理,得BC2=AC2-AB2=602.
∴BC=60.∴CD=2BC=120,
∴学校要受拖拉机噪声影响24 s.
如图有一个长方形零件,根据所给的尺寸(单位,mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解: 过A作垂线,过B作水平线,
两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
强化训练
17.1.2 勾股定理的应用
学习目标(1分钟)
(1)运用勾股定理求线段长度,并从实际问题中建立直角三角形的模型,解决一些简单的实际问题。
自学指导一 (5分钟)
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
提示:
A
B
C
D
1 m
2 m
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.
自学检测一(5分钟)
1.有一个小朋友拿着一根竹竿要通过一个长方
形的门,如果把竹竿竖放就比门高出一尺,斜
放就恰好等于门的对角线,已知门宽四尺,求
竹竿高与门高。
A
B
C
D
4尺
x 尺
解:设门高为x尺,则竹竿长
为(x+1)尺,
根据勾股定理可得x2+42=(x+1)2,
解得 x=7.5
故门高7.5尺,
竹竿高=7.5+1=8.5(尺)
自学指导二 (5分钟)
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?
(提示: )
解:(1)在Rt△AOB中,
根据勾股定理,
OB2=AB2-AO2=2.62-2.42=1
∴OB=1
(2)由题意可得,AC=0.5,OC=2.4-0.5=1.9
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-1.92=3.15
∴OD=
∴BD=OD-OB≈0.77
所以梯子的顶端沿墙下滑0.5m时,梯子底端
并不是也外移0.5m,而是外移约0.77m。
自学检测二(5分钟)
[解析] 设CD=x米,在Rt△ABC中,
可利用勾股定理建立等量关系,
列方程,并解方程求解.
探究问题三 求立体图形中表面上两点之间的最短距离
[解析] 沿长方体表面从点A爬到点B,
考虑路线最短的问题有三种途径:
(1)从右侧面和前面走.
(2)从右侧面和上底面走.
(3)从后侧面和上底面走,
由两点之间线段最短来确定路径.
例4 如图17-1-5所示,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,求这只蚂蚁要爬行的最短距离.
①
②
③
课堂小结 (3分钟)
(1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什么
好的突破办法?利用勾股定理解决实际问题的
注意点是什么?
(3)本节课体现出哪些数学思想方法,都在什么情
况下运用?
当堂训练 (10分钟)
(提示: )
选做题
2.如图所示,公路MN和公路PQ在P点处交会,点A处有一所中学,AP=160 m,点A到公路MN的距离为80 m.假设拖拉机行驶时,周围100 m以内会受到噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响 请说明理由;如果受影响,已知拖拉机的速度为18 km/h,那么学校受影响的时间为多少秒
分析:要判断拖拉机的噪音是否影响学校A,
实质上是看A到公路的距离是否小于100 m;
要求出学校受影响的时间,必须找到拖拉机
行至哪一点开始影响学校,行至哪一点后结束影响学校.
解:学校A到公路MN的距离为80 m,而拖拉机的噪声范围为100 m以内,80<100,故拖拉机会影响学校.如图所示,AB⊥MN,设C,D为公路MN上的两点,且AC=AD=100 m,则拖拉机行驶在CD段时,学校会受到噪声影响.
由题意,得AB=80,AC=100.
由勾股定理,得BC2=AC2-AB2=602.
∴BC=60.∴CD=2BC=120,
∴学校要受拖拉机噪声影响24 s.
