2021—2022学年人教版数学八年级下册18.1.2平行四边形的判定(3) 课件(共15张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册18.1.2平行四边形的判定(3) 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 244.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:40:19 | ||
图片预览





文档简介
(共15张PPT)
动手操作:将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
18.1.2 平行四边形的判定
(第三课时)
学习目标(1分钟)
1、理解三角形中位线的概念,掌握它们的性质;
2、能够熟练地应用三角形的中位线性质进行有、关的证明和计算。
自学指导一(15分钟)
请完成以下操作并猜想DE,BC之间存在怎样的关系:
1、画出一个三角形,记作△ABC,取AB,AC边的中点,分别记为D,E.
2、用直尺分别测量DE,BC的长,比较DE,BC的大小关系,并猜想DE,BC之间存在怎样的数量关系;
3、借助量角器测量有关角的大小,并猜想DE,BC之间的位置关系.
如图,△ABC中,D,E分别是边AB,AC的中点,连接DE.像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
猜想:DE∥BC,且DE = BC .
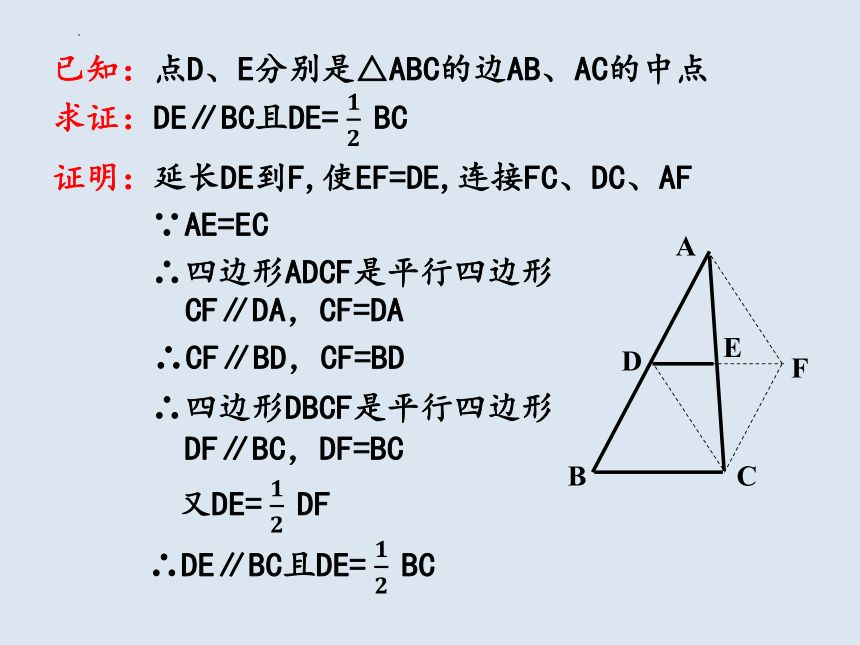
已知:点D、E分别是△ABC的边AB、AC的中点
求证:DE∥BC且DE= BC
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
B
C
A
D
E
F
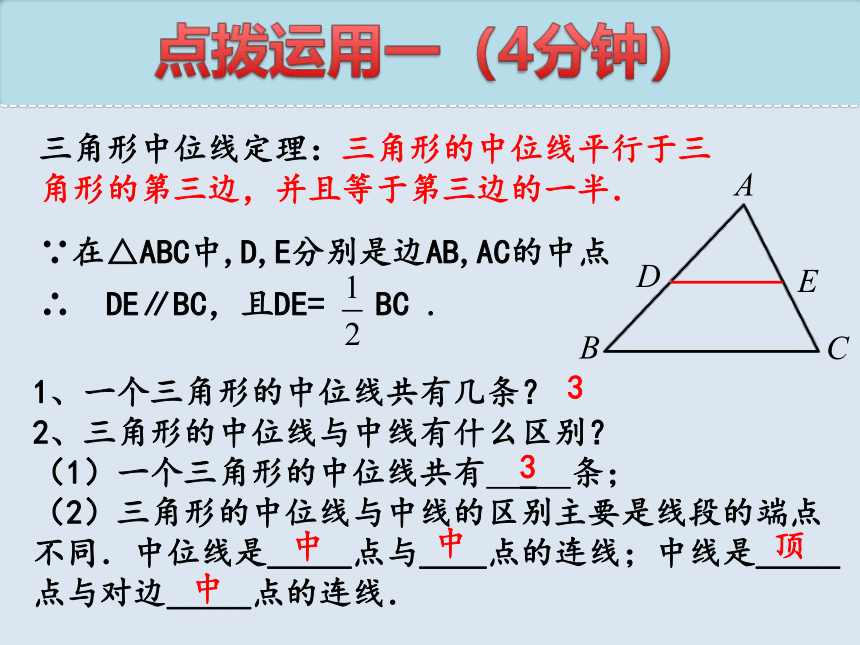
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
∵在△ABC中,D,E分别是边AB,AC的中点
∴ DE∥BC,且DE= BC .
A
B
C
D
E
点拨运用一(4分钟)
1、一个三角形的中位线共有几条?
2、三角形的中位线与中线有什么区别?
(1)一个三角形的中位线共有 _ 条;
(2)三角形的中位线与中线的区别主要是线段的端点不同.中位线是_____点与____点的连线;中线是_____点与对边_____点的连线.
3
中
中
顶
中
3
1、如图1,△ABC中,D、E分别是AB、AC
的中点,BC=10cm,则DE=______.
2、如图1,△ABC中,D、E分别是AB、AC
的中点,∠A=50°, ∠B=70°,则
∠AED=_____.
3、如图,在△ABC中,D、E、F分别是AB、
BC、CA的中点.以这些点为顶点,在图
中,你能画出多少个平
行四边形?为什么?
图1
5cm
60°
E
F
D
F
D
A
C
B
E
F
D
解:3个
自学检测一(8分钟)
4、已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC
在△ACD中
∵G、H分别是CD、DA的中点
∴HG∥AC, HG= AC
同理,EF∥AC, EF= AC
∴HG∥EF, HG=EF
∴四边形EFGH是平行四边形
课堂小结(2分钟)
1、三角形中位线的定义:
____________叫做三角形的
中位线 .
2、三角形的中位线与中线的区别:
中位线是_______的连线;
中线是_______的连线.
3、三角形的中位线定理:三角形的中位线__
于三角形的第三边,并且等于第三边的 __.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
1、如图,在△ABC中,∠C=90°,AC=8,
CB=6,D,E,F分别是BC,AC,AB
的中点,则四边形AEDF的周长为
_____;Rt△ABC的中位线分别是
________;斜边上的中线是____,
其长为_____.
2、如图,D是△ABC内一点,BD⊥CD,
AD=6,BD=4,CD=3,E,F,G,
H分别是边AB,AC,CD,BD的中点,
则四边形EFGH的周长是( )
A.7 B.9 C.10 D.11
18
DE,DF
CF
5
A
B
C
D
E
F
当堂训练(15分钟)
D
3、如图, ABCD的对角线AC, BD交于点O,
点E是AD的中点, △BCD的周长为18,
则△DEO的周长是____
4、如图,已知四边形ABCD中,R,P分别是BC,CD上的
点,E,F分别是AP,RP的中点,当点P在CD上从C向D
移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不变
D.线段EF的长与点P的位置有关
9
C
6、如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点,求证:四边形DECF是平行四边形.
证明:∵点D,E分别为AB,BC边上的中点,
∴DE为△ABC的中位线,
∴DE∥AC.
同理DF∥BC,
即DE∥CF,DF∥EC,
∴四边形DECF是平行四边形.
5、如图,四边形ABCD中,点P是对角线
BD的中点,点E,F分别是AB,CD的中
点,AD=BC,∠PEF=30°,则∠PFE
的度数是( )
A.15° B.20° C.25° D.30°
D
(2014·遂宁)如图,在△ABC中,点A1,B1,C1分别是BC,AC,AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推……若△ABC的周长为1,则△AnBnCn
的周长为____.
选做题
板书设计
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
∵在△ABC中,D,E分别是边AB,AC的中点
∴DE∥BC,且DE= BC .
A
B
C
D
E
动手操作:将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
18.1.2 平行四边形的判定
(第三课时)
学习目标(1分钟)
1、理解三角形中位线的概念,掌握它们的性质;
2、能够熟练地应用三角形的中位线性质进行有、关的证明和计算。
自学指导一(15分钟)
请完成以下操作并猜想DE,BC之间存在怎样的关系:
1、画出一个三角形,记作△ABC,取AB,AC边的中点,分别记为D,E.
2、用直尺分别测量DE,BC的长,比较DE,BC的大小关系,并猜想DE,BC之间存在怎样的数量关系;
3、借助量角器测量有关角的大小,并猜想DE,BC之间的位置关系.
如图,△ABC中,D,E分别是边AB,AC的中点,连接DE.像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
猜想:DE∥BC,且DE = BC .
已知:点D、E分别是△ABC的边AB、AC的中点
求证:DE∥BC且DE= BC
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
B
C
A
D
E
F
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
∵在△ABC中,D,E分别是边AB,AC的中点
∴ DE∥BC,且DE= BC .
A
B
C
D
E
点拨运用一(4分钟)
1、一个三角形的中位线共有几条?
2、三角形的中位线与中线有什么区别?
(1)一个三角形的中位线共有 _ 条;
(2)三角形的中位线与中线的区别主要是线段的端点不同.中位线是_____点与____点的连线;中线是_____点与对边_____点的连线.
3
中
中
顶
中
3
1、如图1,△ABC中,D、E分别是AB、AC
的中点,BC=10cm,则DE=______.
2、如图1,△ABC中,D、E分别是AB、AC
的中点,∠A=50°, ∠B=70°,则
∠AED=_____.
3、如图,在△ABC中,D、E、F分别是AB、
BC、CA的中点.以这些点为顶点,在图
中,你能画出多少个平
行四边形?为什么?
图1
5cm
60°
E
F
D
F
D
A
C
B
E
F
D
解:3个
自学检测一(8分钟)
4、已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC
在△ACD中
∵G、H分别是CD、DA的中点
∴HG∥AC, HG= AC
同理,EF∥AC, EF= AC
∴HG∥EF, HG=EF
∴四边形EFGH是平行四边形
课堂小结(2分钟)
1、三角形中位线的定义:
____________叫做三角形的
中位线 .
2、三角形的中位线与中线的区别:
中位线是_______的连线;
中线是_______的连线.
3、三角形的中位线定理:三角形的中位线__
于三角形的第三边,并且等于第三边的 __.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
1、如图,在△ABC中,∠C=90°,AC=8,
CB=6,D,E,F分别是BC,AC,AB
的中点,则四边形AEDF的周长为
_____;Rt△ABC的中位线分别是
________;斜边上的中线是____,
其长为_____.
2、如图,D是△ABC内一点,BD⊥CD,
AD=6,BD=4,CD=3,E,F,G,
H分别是边AB,AC,CD,BD的中点,
则四边形EFGH的周长是( )
A.7 B.9 C.10 D.11
18
DE,DF
CF
5
A
B
C
D
E
F
当堂训练(15分钟)
D
3、如图, ABCD的对角线AC, BD交于点O,
点E是AD的中点, △BCD的周长为18,
则△DEO的周长是____
4、如图,已知四边形ABCD中,R,P分别是BC,CD上的
点,E,F分别是AP,RP的中点,当点P在CD上从C向D
移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不变
D.线段EF的长与点P的位置有关
9
C
6、如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点,求证:四边形DECF是平行四边形.
证明:∵点D,E分别为AB,BC边上的中点,
∴DE为△ABC的中位线,
∴DE∥AC.
同理DF∥BC,
即DE∥CF,DF∥EC,
∴四边形DECF是平行四边形.
5、如图,四边形ABCD中,点P是对角线
BD的中点,点E,F分别是AB,CD的中
点,AD=BC,∠PEF=30°,则∠PFE
的度数是( )
A.15° B.20° C.25° D.30°
D
(2014·遂宁)如图,在△ABC中,点A1,B1,C1分别是BC,AC,AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推……若△ABC的周长为1,则△AnBnCn
的周长为____.
选做题
板书设计
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
∵在△ABC中,D,E分别是边AB,AC的中点
∴DE∥BC,且DE= BC .
A
B
C
D
E
