2021—2022学年人教版数学八年级下册19.1.1变量与函数(1)课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.1.1变量与函数(1)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:42:09 | ||
图片预览





文档简介
(共17张PPT)
直角三角形中一个锐角的度数y与另一个锐角的度数x之间的关系为( )
A.y=180°-x(0°<x<90°)
B.y=90°-x(0°<x<90°)
C.y=180°-x(0°≤x≤90°)
D.y=90°-x(0°≤x≤90°)
B
19.1.1 变量与函数
(第一课时)
学习目标(1分钟)
1、了解变量与常量的意义;
2、从典型实例中抽象概括出变量与常量的概念;
自学指导一(10分钟)
汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时.
60
120
180
240
300
问题一:
(1)请同学们根据题意填写下表:
(2)用含有t的式子表示s为__________;
(3)在(2)的式子中,数值没有发生变化的量是____,数值发生变化的量是________.
t/小时 1 2 3 4 5
s/千米
s=60t
60
s,t
每张电影票的售价为10元,如果早场售出票150张,日场售出205张,晚场售出310张,三场电影票的票房收入各多少元?
若设一场电影售出票 x 张,票房收入为 y 元,怎样用含 x 的式子表示 y ?
问题二:
票房收入 = 售价×售票张数
早场票房收入 = 10×150 = 1500 (元)
日场票房收入 = 10×205 = 2050 (元)
晚场票房收入 = 10×310 = 3100 (元)
y = 10x
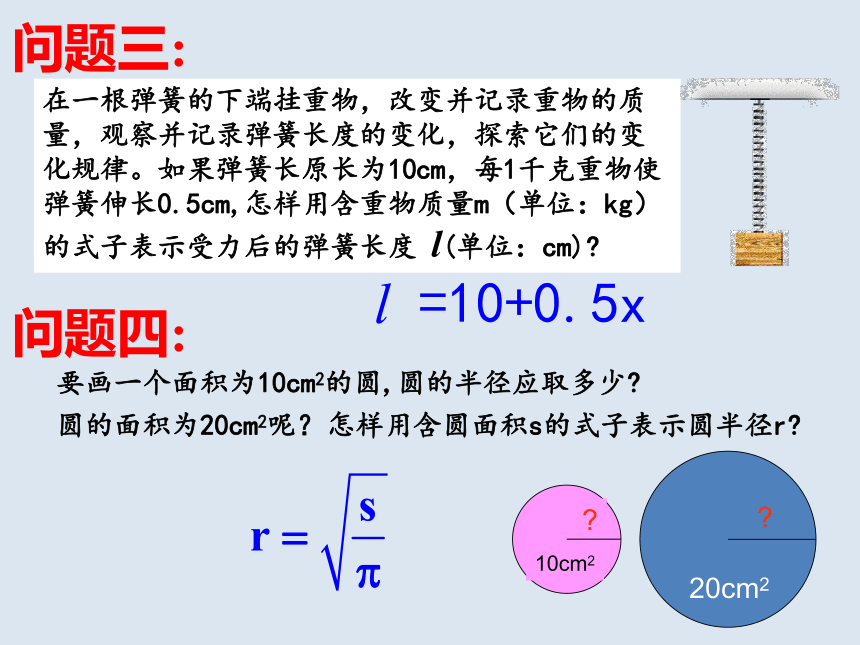
在一根弹簧的下端挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律。如果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,怎样用含重物质量m(单位:kg)的式子表示受力后的弹簧长度 l(单位:cm)
l =10+0.5x
问题三:
问题四:
要画一个面积为10cm2的圆,圆的半径应取多少
10cm2
圆的面积为20cm2呢?
怎样用含圆面积s的式子表示圆半径r
20cm2
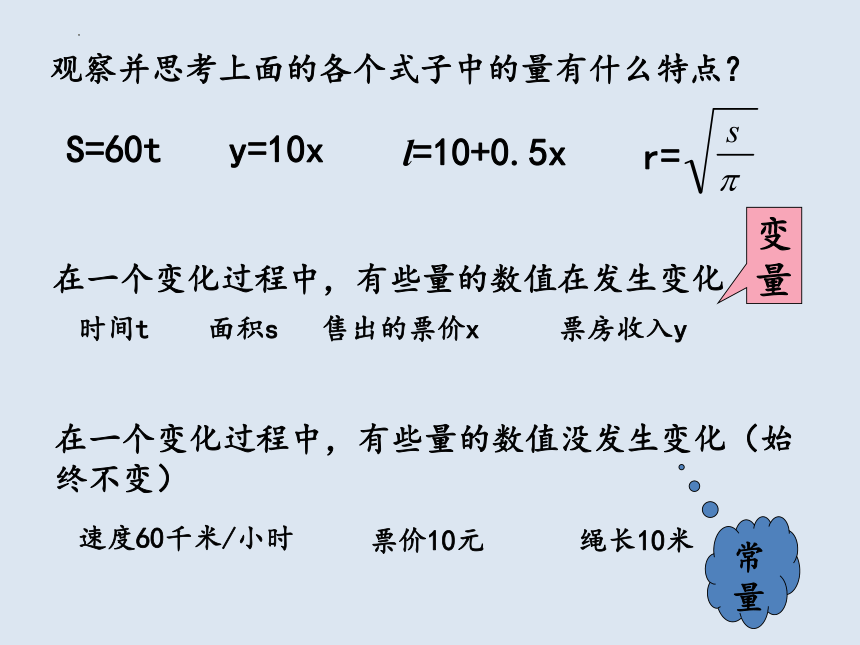
观察并思考上面的各个式子中的量有什么特点?
在一个变化过程中,有些量的数值在发生变化
在一个变化过程中,有些量的数值没发生变化(始终不变)
变量
常量
时间t
面积s
售出的票价x
票房收入y
速度60千米/小时
票价10元
绳长10米
S=60t
y=10x
r=
l=10+0.5x
点拨运用一(5分钟)
[归纳]一个变化过程中的量,包含变量和常量.常量不等于常数,它可以是数值不变的字母.如在匀速运动中的速度v就是一个常量.变量随不同的问题而有所不同,在这个式子中是变量,也许在其他式子中就是常量,因此常量和变量是相对的,是视具体问题而定的.
定义:
在一个变化过程中,我们称数值发生变化的量为变量.
有些数值始终不变的我们称之为常量.
自学检测一(5分钟)
1.学校购买某种型号的钢笔作为学生的奖
品,钢笔的单价是4元/支,则总金额y(元)与购
买支数x(支)的关系式是 ,
其中变量是 ,常量是 .
2.计划购买50元的乒乓球,所能购买的总数
n(个)与单价 a(元)的关系式是 ,
其中变量是 ,常量是 .
y = 4x
x , y
4
a ,n
50
探究问题 研究一些变量间的变化规律
例 某超市售货时,其销售数量x与售价y如下表所示,请你根据表中所提供的信息列出y与x之间的关系式,指出变量与常量,并求当销售数量为2.5千克时的售价是多少元.
销售数 量x(千克) 1 2 3 4 5 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 40+2.0 …
[解析] 根据表中售价随销售数量变化的关系,发现销售数量每增加1千克,售价增加8.4元.
解:y=8.4x,其中常量为8.4,变量为x,y.
当销售数量为2.5千克时,售价是21元.
点拨运用二(8分钟)
[归纳总结] “万物皆变”,有些运动变化找不到变量之间的依赖关系,但是有些运动变化现象中变量之间存在依赖关系,这样就可以用一个变量表示出另一个变量.形如“a+b”式的关系式在寻找变量间关系时,一般拆成两部分:“+”号前部分和“+”号后部分,针对两部分分别找规律,然后汇总.
课堂小结(1分钟)
在一个变化过程中,我们称数值发生变化的量为变量
有些数值始终不变的我们称之为常量.
当堂训练(10分钟)
1、某型号的汽车在路面上的制动距离s = ,其中变量是( )
A.s,v B.s, C.s D.v
2、购买一些签字笔,单价3元,总价为y元,签字笔为x支,y随x变化的关系式y= , 是变量,
是常量.
A
3x
x,y
3
3、王老师讲完“变量与常量”后,让同学们说出几个实际生活中的例子,并指出其中的常量和变量.
甲生说:“如果设路程为s(km),速度为v(km/h),时间为t(h),当s为一定值时,s为常量,v,t为变量.”
乙生说:“甲生所举实例中,当t为一定值时,t为常量,s,v为变量.”
丙生说:“甲生所举实例中,当v为一定值时,v为常量,s,t为变量.”
你认为哪一位同学的说法是正确的?
解:三位同学的说法都是正确的.
4、下表给出了橘农王林去年橘子的销售额y(元)随橘子卖出质量x(kg)的变化的有关数据:
(1)上表反映了哪两个变量之间 的关系 并写出函数的解析式.
(2) 是变量 是常量
(3)当橘子卖出5kg时,销售额是多少
(4)估计当橘子卖出50kg时,销售额是多少
卖出质量(kg) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
y = 2x
x、y
2
y=2×5=10(元)
y=2×50=100(元)
选做题
如图中,每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为S,按图的排列规律推断S与n之间的关系可以用式子________________来表示.
板书设计
在一个变化过程中,我们称数值发生变化的量为变量
有些数值始终不变的我们称之为常量.
直角三角形中一个锐角的度数y与另一个锐角的度数x之间的关系为( )
A.y=180°-x(0°<x<90°)
B.y=90°-x(0°<x<90°)
C.y=180°-x(0°≤x≤90°)
D.y=90°-x(0°≤x≤90°)
B
19.1.1 变量与函数
(第一课时)
学习目标(1分钟)
1、了解变量与常量的意义;
2、从典型实例中抽象概括出变量与常量的概念;
自学指导一(10分钟)
汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时.
60
120
180
240
300
问题一:
(1)请同学们根据题意填写下表:
(2)用含有t的式子表示s为__________;
(3)在(2)的式子中,数值没有发生变化的量是____,数值发生变化的量是________.
t/小时 1 2 3 4 5
s/千米
s=60t
60
s,t
每张电影票的售价为10元,如果早场售出票150张,日场售出205张,晚场售出310张,三场电影票的票房收入各多少元?
若设一场电影售出票 x 张,票房收入为 y 元,怎样用含 x 的式子表示 y ?
问题二:
票房收入 = 售价×售票张数
早场票房收入 = 10×150 = 1500 (元)
日场票房收入 = 10×205 = 2050 (元)
晚场票房收入 = 10×310 = 3100 (元)
y = 10x
在一根弹簧的下端挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律。如果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,怎样用含重物质量m(单位:kg)的式子表示受力后的弹簧长度 l(单位:cm)
l =10+0.5x
问题三:
问题四:
要画一个面积为10cm2的圆,圆的半径应取多少
10cm2
圆的面积为20cm2呢?
怎样用含圆面积s的式子表示圆半径r
20cm2
观察并思考上面的各个式子中的量有什么特点?
在一个变化过程中,有些量的数值在发生变化
在一个变化过程中,有些量的数值没发生变化(始终不变)
变量
常量
时间t
面积s
售出的票价x
票房收入y
速度60千米/小时
票价10元
绳长10米
S=60t
y=10x
r=
l=10+0.5x
点拨运用一(5分钟)
[归纳]一个变化过程中的量,包含变量和常量.常量不等于常数,它可以是数值不变的字母.如在匀速运动中的速度v就是一个常量.变量随不同的问题而有所不同,在这个式子中是变量,也许在其他式子中就是常量,因此常量和变量是相对的,是视具体问题而定的.
定义:
在一个变化过程中,我们称数值发生变化的量为变量.
有些数值始终不变的我们称之为常量.
自学检测一(5分钟)
1.学校购买某种型号的钢笔作为学生的奖
品,钢笔的单价是4元/支,则总金额y(元)与购
买支数x(支)的关系式是 ,
其中变量是 ,常量是 .
2.计划购买50元的乒乓球,所能购买的总数
n(个)与单价 a(元)的关系式是 ,
其中变量是 ,常量是 .
y = 4x
x , y
4
a ,n
50
探究问题 研究一些变量间的变化规律
例 某超市售货时,其销售数量x与售价y如下表所示,请你根据表中所提供的信息列出y与x之间的关系式,指出变量与常量,并求当销售数量为2.5千克时的售价是多少元.
销售数 量x(千克) 1 2 3 4 5 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 40+2.0 …
[解析] 根据表中售价随销售数量变化的关系,发现销售数量每增加1千克,售价增加8.4元.
解:y=8.4x,其中常量为8.4,变量为x,y.
当销售数量为2.5千克时,售价是21元.
点拨运用二(8分钟)
[归纳总结] “万物皆变”,有些运动变化找不到变量之间的依赖关系,但是有些运动变化现象中变量之间存在依赖关系,这样就可以用一个变量表示出另一个变量.形如“a+b”式的关系式在寻找变量间关系时,一般拆成两部分:“+”号前部分和“+”号后部分,针对两部分分别找规律,然后汇总.
课堂小结(1分钟)
在一个变化过程中,我们称数值发生变化的量为变量
有些数值始终不变的我们称之为常量.
当堂训练(10分钟)
1、某型号的汽车在路面上的制动距离s = ,其中变量是( )
A.s,v B.s, C.s D.v
2、购买一些签字笔,单价3元,总价为y元,签字笔为x支,y随x变化的关系式y= , 是变量,
是常量.
A
3x
x,y
3
3、王老师讲完“变量与常量”后,让同学们说出几个实际生活中的例子,并指出其中的常量和变量.
甲生说:“如果设路程为s(km),速度为v(km/h),时间为t(h),当s为一定值时,s为常量,v,t为变量.”
乙生说:“甲生所举实例中,当t为一定值时,t为常量,s,v为变量.”
丙生说:“甲生所举实例中,当v为一定值时,v为常量,s,t为变量.”
你认为哪一位同学的说法是正确的?
解:三位同学的说法都是正确的.
4、下表给出了橘农王林去年橘子的销售额y(元)随橘子卖出质量x(kg)的变化的有关数据:
(1)上表反映了哪两个变量之间 的关系 并写出函数的解析式.
(2) 是变量 是常量
(3)当橘子卖出5kg时,销售额是多少
(4)估计当橘子卖出50kg时,销售额是多少
卖出质量(kg) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
y = 2x
x、y
2
y=2×5=10(元)
y=2×50=100(元)
选做题
如图中,每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为S,按图的排列规律推断S与n之间的关系可以用式子________________来表示.
板书设计
在一个变化过程中,我们称数值发生变化的量为变量
有些数值始终不变的我们称之为常量.
