2021—2022学年人教版数学八年级下册19.1.2函数的图像(1)课件(共16张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.1.2函数的图像(1)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:43:21 | ||
图片预览






文档简介
(共16张PPT)
函数表示方法:
(1)解析式法(关系式法)
(2)列表法
(3)图象法
表示函数关系的方法:
1、解析法:准确地反映了函数与自变量之间的数量关系。
2、列表法:具体地反映了函数与自变量的数值对应关系。
3、图象法:直观地反映了函数随自变量的变化而变化的规律。
-3
4
14
24
O
t/时
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
第十九章 一次函数
19.1 函数
19.1.2 函数的图象
第1课时 函数图象及其画法
学习目标 (1分钟)
1、认识函数图像;会从函数图像中读取信息。
2、从实际问题中分析函数图像。
自学指导一(5分钟)
[答案] 给自变量一个值,就得到一个相应的函数值,从而形成了一对有序实数对(x,S).点的横坐标对应了自变量的值,点的纵坐标对应了函数值.
2.表示x与S的对应关系的点有_________个,我们描出的点是有限的,其他的点需要想象出来.然后利用平滑的曲线将描出的各点连接起来.不在曲线上的点用___________表示,在曲线上的点用小黑点表示.
无数
空心圈
定义:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的________________,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
横、纵坐标
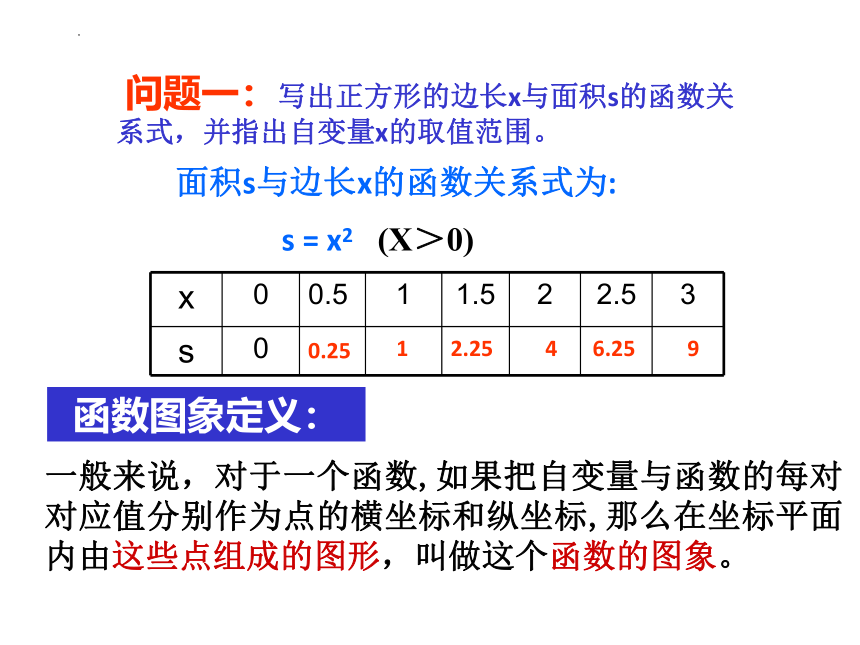
问题一:写出正方形的边长x与面积s的函数关系式,并指出自变量x的取值范围。
面积s与边长x的函数关系式为:
s = x2 (X>0)
x 0 0.5 1 1.5 2 2.5 3
s 0
0.25
1
2.25
4
6.25
9
函数图象定义:
一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么在坐标平面内由这些点组成的图形,叫做这个函数的图象。
自学检测一(3分钟)
C
点拨运用一(3分钟)
.
如何判断一点是否在某个函数的图象上
若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在。
自学指导二(5分钟)
知识点二 函数图象的画法
画函数图象的一般步骤:_______、______、______.
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
列表
描点
连线
自学检测二(5分钟)
探究问题二 画函数图象
点拨运用二(5分钟)
[归纳总结] 画函数图象时要注意:
(1)应先考虑自变量的取值范围.有的函数自变量不受限制,取值
范围为全体实数,这时在列表对自变量取值时,一般以0为中心对自变量对称取值,使得画出的图形更美观,也能更好地反映函数的变化趋势;有的函数自变量取值受到解析式本身的限制或按要求对自变量取值,这时在列表求对应值时应具体问题具体分析.
(2)在描点连线时,应用平滑的曲线按自变量由小到大(或由大到小)的顺序把所描出的各点连接起来,需要注意的是在连线时应根据x的取值范围向能够延伸的端点处延伸.
课堂小结(1分钟)
1、函数的图象的定义。
2、画函数图象的步骤:
(1)列表;(2)描点;(3)连线。
3、图象的变化趋势。
当堂训练(10分钟)
1.(2013 重庆)万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州.若该轮船从万州出发后所用的时间为x(小时),轮船距万州的距离为y(千米),则下列各图形中,能够反映y与x之间函数关系的大致图象是( )
2.(2013 玉林)均匀地向一个瓶子注水,最后 把瓶子注满.在注水过程中,水面高度h随 时间t的变化规律如图2所示,则这个瓶子的形状是下列的( )
C
B
3.(2013 湘西州)小芳的爷爷每天坚持体育锻炼,某天他慢步行走到离家较远的公园,打了一会儿太极拳,然后沿原路跑步到家里,下面能够反映当天小芳爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
4. 已知函数:y=2x-1,下列各点:(1)(1,1),(2)(-1,-1),(3)(-1,-3),(4)(2,3). 在函数图象上的有( )
A. 1个 B. 2个 C. 3个 D. 4个
5. 请画函数:y= 的图象,该图象与x轴有交点吗?为什么?
C
C
解:图略,没有,因为x的值不能为0.
板书设计
1、函数的图象的定义。
2、画函数图象的步骤:
(1)列表;(2)描点;(3)连线。
3、图象的变化趋势。
函数表示方法:
(1)解析式法(关系式法)
(2)列表法
(3)图象法
表示函数关系的方法:
1、解析法:准确地反映了函数与自变量之间的数量关系。
2、列表法:具体地反映了函数与自变量的数值对应关系。
3、图象法:直观地反映了函数随自变量的变化而变化的规律。
-3
4
14
24
O
t/时
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
第十九章 一次函数
19.1 函数
19.1.2 函数的图象
第1课时 函数图象及其画法
学习目标 (1分钟)
1、认识函数图像;会从函数图像中读取信息。
2、从实际问题中分析函数图像。
自学指导一(5分钟)
[答案] 给自变量一个值,就得到一个相应的函数值,从而形成了一对有序实数对(x,S).点的横坐标对应了自变量的值,点的纵坐标对应了函数值.
2.表示x与S的对应关系的点有_________个,我们描出的点是有限的,其他的点需要想象出来.然后利用平滑的曲线将描出的各点连接起来.不在曲线上的点用___________表示,在曲线上的点用小黑点表示.
无数
空心圈
定义:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的________________,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
横、纵坐标
问题一:写出正方形的边长x与面积s的函数关系式,并指出自变量x的取值范围。
面积s与边长x的函数关系式为:
s = x2 (X>0)
x 0 0.5 1 1.5 2 2.5 3
s 0
0.25
1
2.25
4
6.25
9
函数图象定义:
一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么在坐标平面内由这些点组成的图形,叫做这个函数的图象。
自学检测一(3分钟)
C
点拨运用一(3分钟)
.
如何判断一点是否在某个函数的图象上
若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在。
自学指导二(5分钟)
知识点二 函数图象的画法
画函数图象的一般步骤:_______、______、______.
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
列表
描点
连线
自学检测二(5分钟)
探究问题二 画函数图象
点拨运用二(5分钟)
[归纳总结] 画函数图象时要注意:
(1)应先考虑自变量的取值范围.有的函数自变量不受限制,取值
范围为全体实数,这时在列表对自变量取值时,一般以0为中心对自变量对称取值,使得画出的图形更美观,也能更好地反映函数的变化趋势;有的函数自变量取值受到解析式本身的限制或按要求对自变量取值,这时在列表求对应值时应具体问题具体分析.
(2)在描点连线时,应用平滑的曲线按自变量由小到大(或由大到小)的顺序把所描出的各点连接起来,需要注意的是在连线时应根据x的取值范围向能够延伸的端点处延伸.
课堂小结(1分钟)
1、函数的图象的定义。
2、画函数图象的步骤:
(1)列表;(2)描点;(3)连线。
3、图象的变化趋势。
当堂训练(10分钟)
1.(2013 重庆)万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州.若该轮船从万州出发后所用的时间为x(小时),轮船距万州的距离为y(千米),则下列各图形中,能够反映y与x之间函数关系的大致图象是( )
2.(2013 玉林)均匀地向一个瓶子注水,最后 把瓶子注满.在注水过程中,水面高度h随 时间t的变化规律如图2所示,则这个瓶子的形状是下列的( )
C
B
3.(2013 湘西州)小芳的爷爷每天坚持体育锻炼,某天他慢步行走到离家较远的公园,打了一会儿太极拳,然后沿原路跑步到家里,下面能够反映当天小芳爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
4. 已知函数:y=2x-1,下列各点:(1)(1,1),(2)(-1,-1),(3)(-1,-3),(4)(2,3). 在函数图象上的有( )
A. 1个 B. 2个 C. 3个 D. 4个
5. 请画函数:y= 的图象,该图象与x轴有交点吗?为什么?
C
C
解:图略,没有,因为x的值不能为0.
板书设计
1、函数的图象的定义。
2、画函数图象的步骤:
(1)列表;(2)描点;(3)连线。
3、图象的变化趋势。
