2021—2022学年人教版数学八年级下册19.2.1正比例函数(2) 课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.2.1正比例函数(2) 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 356.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:44:17 | ||
图片预览




文档简介
(共18张PPT)
1、一般地,形如 ______( 是常数, )的函数叫做正比例函数,其中 叫做___________ .
2、若 是正比例函数,则m= .
y=kx
k
k≠0
k
比例系数
3
3、已知函数y=kx,当 =-1时, =6,则 与 之间的函数关系为 ____________ .
4、用描点法画函数图象有哪几个步骤?
(1)_______,(2)_______,(3)_______.
y=-6x
列表
描点
连线
19.2.1 正比例函数
(第二课时)
学习目标(1分钟)
1、会画正比例函数的图象;
2、能根据正比例函数的图象和表达式 y =kx(k≠0)理解k>0和k<0时,函数的图象特征与增减性;
3、通过观察图象、归纳总结概括出正比例函数性质的活动,发展数学感知、数学表征、数学概括能力,体会数形结合的思想,发展几何直观.
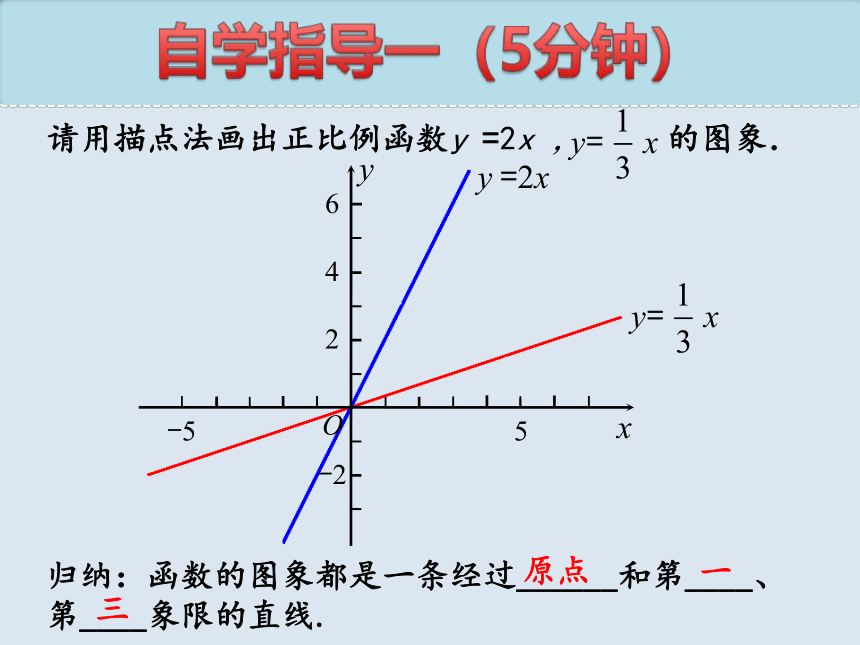
自学指导一(5分钟)
请用描点法画出正比例函数y =2x , 的图象.
y =2x
6
4
2
-2
-5
5
x
y
O
归纳:函数的图象都是一条经过______和第____、第____象限的直线.
原点
一
三
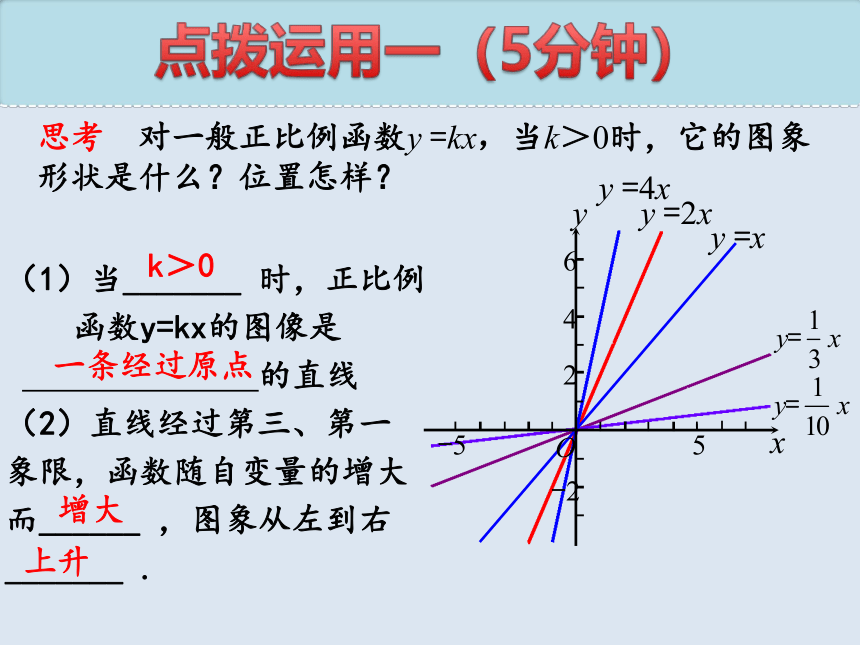
点拨运用一(5分钟)
思考 对一般正比例函数y =kx,当k>0时,它的图象形状是什么?位置怎样?
y =2x
y =x
y =4x
6
4
2
-2
-5
5
x
y
O
(1)当_______ 时,正比例
函数y=kx的图像是
的直线
(2)直线经过第三、第一
象限,函数随自变量的增大
而______ ,图象从左到右
_______ .
k>0
增大
上升
一条经过原点
B
2、正比例函数 的图象经过一、三象限,则m的取值范围是( )
A. m=1 B. m>1 C. m<1 D.m≥1
1、对于正比例函数y =kx,当x 增大时,y 随x
的增大而增大,则k的取值范围 ( ).
A.k<0 B.k≤0
C.k>0 D.k≥0
C
自学检测一(4分钟)
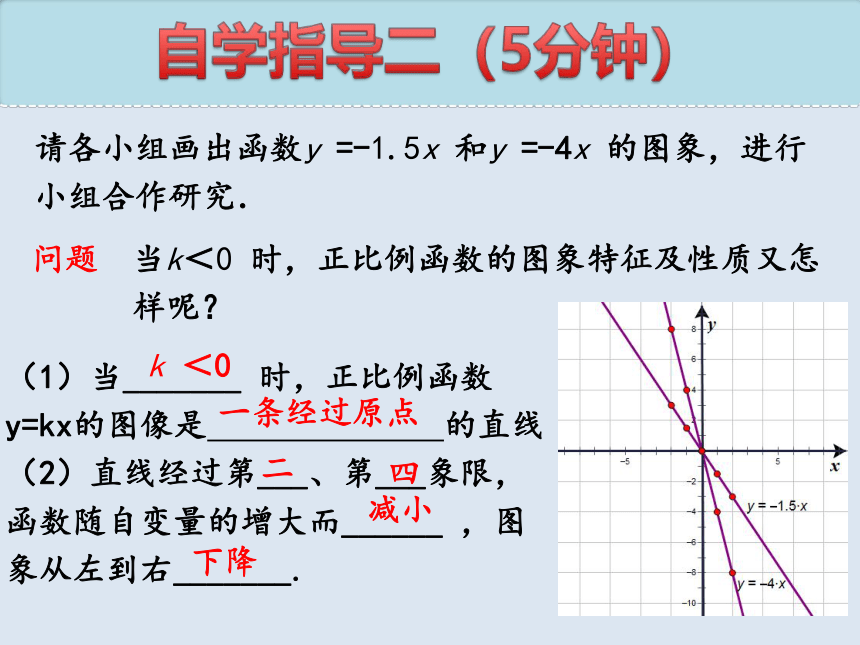
请各小组画出函数y =-1.5x 和y =-4x 的图象,进行
小组合作研究.
问题 当k<0 时,正比例函数的图象特征及性质又怎
样呢?
自学指导二(5分钟)
(1)当_______ 时,正比例函数y=kx的图像是 的直线
(2)直线经过第___、第___象限,函数随自变量的增大而______ ,图象从左到右_______.
k <0
减小
下降
一条经过原点
二
四
正比例函数的性质:
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
问题 我们知道,正比例函数的图象是一条经过坐标原点的直线,我们也知道,两点确定一条直线,现在,我们有画正比例函数图象的简便画法了吗?
点拨运用二(5分钟)
解:因为两点确定一条直线,所以可用两点法画正比例函数 ( )的图象.一般地,过原点和(1,k)(k是常数,k≠0)的直线,即正比例函数 ( )的图象.
因为两点确定一条直线,所以经过原点与点( , )( 是常数, )的直线,即是正比例函数 ( )的图象.
结论
1
k
k
k≠0
自学检测二(5分钟)
1、函数y=-5x的图象在第_______ 象限内,经过点(0, )与点(1, ),y随x的增大而________ .
二、四
0
-5
减小
2、在平面直角坐标系中,正比例函数y =kx(k<0)的图象的大致位置只可能是( ).
x
y
O
x
y
O
x
y
O
x
y
O
A
B
C
D
A
3、下列函数① , ② ,
③ , ④ ,⑤ 中,
y随x的增大而减小函数是__________ ,
y随x的增大而增大的函数是__________ .
②④⑤
①③
课堂小结(2分钟)
3、最简单画正比例函数图象的方法:
⑴在平面直角坐标系只选取两点:(0, )与点(1, );
⑵把这两点连成一条______,这条直线就是正比例函数y=kx(k≠0)的图象.
0
k
直线
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
当堂训练(10分钟)
1、函数y=-5x的图象在第_________象限内,经过点(0, )与点(1, ),y随x的增大而_______.
2、正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A. m=1 B. m>1 C. m<1 D.m≥1
二、四
0
B
-5
减小
3、已知关于x的正比例函数y=(3-k)x.
(1)若y的值随x的增大而增大,则k的取值范围是什么?
(2)若y的值随x的增大而减小,则k的取值范围是什么?
解:(1)当3-k>0,即k<3时,y的值随x的增大而增大.
(2)当3-k<0,即k>3时,y的值随x的增大而减小.
4、正比例函数y=-4x,y=4x,y=x的图象的共同点是( )
A.经过同样的象限 B.都是过原点的直线
C.从左到右上升 D.从左到右下降
5、对于函数y=x(k是常数,k≠0)的图象,下列说法不正确的是( )
A.是一条直线
B.过点( ,k)
C.经过第一、三象限或第二、四象限
D.y随着x的增大而增大
B
C
[归纳总结] 正比例函数的定义以及正比例函数的性质中,所隐含的条件常常用来确定字母的取值或者用来比较函数值的大小.通常存在已知图象经过的象限、函数值随自变量值的变化关系以及比例系数k的符号之一,可以得出另外两个相应的结论.比较函数值大小时,图象法要优于其他方法.已知函数解析式及其图象上点的横坐标,比较点的纵坐标的值的方法有三种:
①代入法,准确,但需要计算;
②图象法,直观形象,但需要画图;
③函数性质法,是三种方法里面最简便的一种.
比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
k1<k2 <k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
选做题
板书设计
3、最简单画正比例函数图象的方法:
⑴在平面直角坐标系只选取两点:(0, )与点(1, );
⑵把这两点连成一条______,这条直线就是正比例函数y=kx(k≠0)的图象.
0
k
直线
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
1、一般地,形如 ______( 是常数, )的函数叫做正比例函数,其中 叫做___________ .
2、若 是正比例函数,则m= .
y=kx
k
k≠0
k
比例系数
3
3、已知函数y=kx,当 =-1时, =6,则 与 之间的函数关系为 ____________ .
4、用描点法画函数图象有哪几个步骤?
(1)_______,(2)_______,(3)_______.
y=-6x
列表
描点
连线
19.2.1 正比例函数
(第二课时)
学习目标(1分钟)
1、会画正比例函数的图象;
2、能根据正比例函数的图象和表达式 y =kx(k≠0)理解k>0和k<0时,函数的图象特征与增减性;
3、通过观察图象、归纳总结概括出正比例函数性质的活动,发展数学感知、数学表征、数学概括能力,体会数形结合的思想,发展几何直观.
自学指导一(5分钟)
请用描点法画出正比例函数y =2x , 的图象.
y =2x
6
4
2
-2
-5
5
x
y
O
归纳:函数的图象都是一条经过______和第____、第____象限的直线.
原点
一
三
点拨运用一(5分钟)
思考 对一般正比例函数y =kx,当k>0时,它的图象形状是什么?位置怎样?
y =2x
y =x
y =4x
6
4
2
-2
-5
5
x
y
O
(1)当_______ 时,正比例
函数y=kx的图像是
的直线
(2)直线经过第三、第一
象限,函数随自变量的增大
而______ ,图象从左到右
_______ .
k>0
增大
上升
一条经过原点
B
2、正比例函数 的图象经过一、三象限,则m的取值范围是( )
A. m=1 B. m>1 C. m<1 D.m≥1
1、对于正比例函数y =kx,当x 增大时,y 随x
的增大而增大,则k的取值范围 ( ).
A.k<0 B.k≤0
C.k>0 D.k≥0
C
自学检测一(4分钟)
请各小组画出函数y =-1.5x 和y =-4x 的图象,进行
小组合作研究.
问题 当k<0 时,正比例函数的图象特征及性质又怎
样呢?
自学指导二(5分钟)
(1)当_______ 时,正比例函数y=kx的图像是 的直线
(2)直线经过第___、第___象限,函数随自变量的增大而______ ,图象从左到右_______.
k <0
减小
下降
一条经过原点
二
四
正比例函数的性质:
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
问题 我们知道,正比例函数的图象是一条经过坐标原点的直线,我们也知道,两点确定一条直线,现在,我们有画正比例函数图象的简便画法了吗?
点拨运用二(5分钟)
解:因为两点确定一条直线,所以可用两点法画正比例函数 ( )的图象.一般地,过原点和(1,k)(k是常数,k≠0)的直线,即正比例函数 ( )的图象.
因为两点确定一条直线,所以经过原点与点( , )( 是常数, )的直线,即是正比例函数 ( )的图象.
结论
1
k
k
k≠0
自学检测二(5分钟)
1、函数y=-5x的图象在第_______ 象限内,经过点(0, )与点(1, ),y随x的增大而________ .
二、四
0
-5
减小
2、在平面直角坐标系中,正比例函数y =kx(k<0)的图象的大致位置只可能是( ).
x
y
O
x
y
O
x
y
O
x
y
O
A
B
C
D
A
3、下列函数① , ② ,
③ , ④ ,⑤ 中,
y随x的增大而减小函数是__________ ,
y随x的增大而增大的函数是__________ .
②④⑤
①③
课堂小结(2分钟)
3、最简单画正比例函数图象的方法:
⑴在平面直角坐标系只选取两点:(0, )与点(1, );
⑵把这两点连成一条______,这条直线就是正比例函数y=kx(k≠0)的图象.
0
k
直线
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
当堂训练(10分钟)
1、函数y=-5x的图象在第_________象限内,经过点(0, )与点(1, ),y随x的增大而_______.
2、正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A. m=1 B. m>1 C. m<1 D.m≥1
二、四
0
B
-5
减小
3、已知关于x的正比例函数y=(3-k)x.
(1)若y的值随x的增大而增大,则k的取值范围是什么?
(2)若y的值随x的增大而减小,则k的取值范围是什么?
解:(1)当3-k>0,即k<3时,y的值随x的增大而增大.
(2)当3-k<0,即k>3时,y的值随x的增大而减小.
4、正比例函数y=-4x,y=4x,y=x的图象的共同点是( )
A.经过同样的象限 B.都是过原点的直线
C.从左到右上升 D.从左到右下降
5、对于函数y=x(k是常数,k≠0)的图象,下列说法不正确的是( )
A.是一条直线
B.过点( ,k)
C.经过第一、三象限或第二、四象限
D.y随着x的增大而增大
B
C
[归纳总结] 正比例函数的定义以及正比例函数的性质中,所隐含的条件常常用来确定字母的取值或者用来比较函数值的大小.通常存在已知图象经过的象限、函数值随自变量值的变化关系以及比例系数k的符号之一,可以得出另外两个相应的结论.比较函数值大小时,图象法要优于其他方法.已知函数解析式及其图象上点的横坐标,比较点的纵坐标的值的方法有三种:
①代入法,准确,但需要计算;
②图象法,直观形象,但需要画图;
③函数性质法,是三种方法里面最简便的一种.
比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
k1<k2 <k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
选做题
板书设计
3、最简单画正比例函数图象的方法:
⑴在平面直角坐标系只选取两点:(0, )与点(1, );
⑵把这两点连成一条______,这条直线就是正比例函数y=kx(k≠0)的图象.
0
k
直线
1、图像: 正比例函数y= kx (k是常数,k≠0) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
2、性质:当k>0时,直线y= kx经过第一、三象限,从左向右上升,即y随着x的增大而增大;
当k<0时,直线y= kx经过第二、四象限,从左向右下降,即y随着x的增大而减小。
