人教版八年级下册19.2.3一次函数与方程、不等式(第2课时)课件(共17张PPT)
文档属性
| 名称 | 人教版八年级下册19.2.3一次函数与方程、不等式(第2课时)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:43:53 | ||
图片预览



文档简介
(共17张PPT)
19.2.3 一次函数与方程、不等式
第2课时
知识回顾
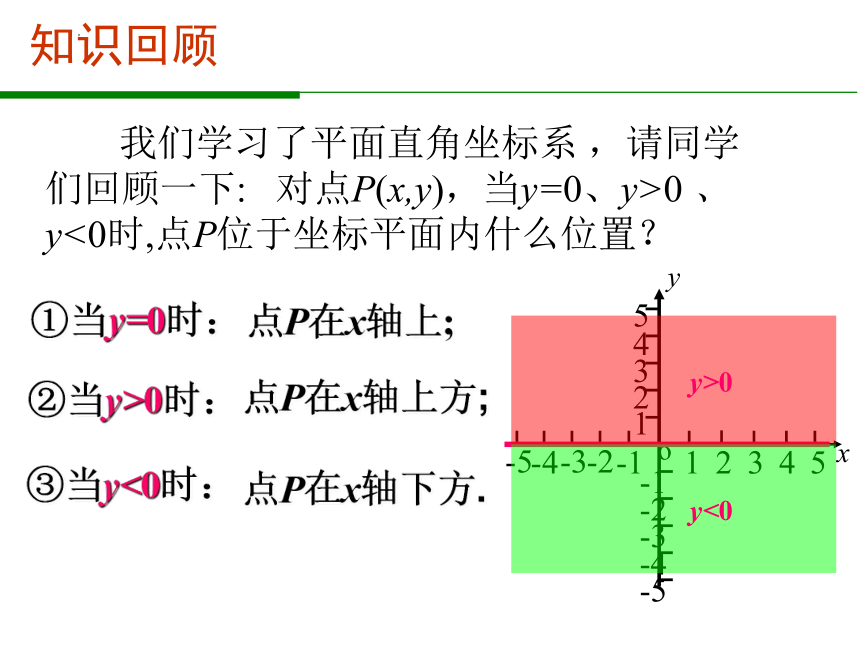
我们学面直角坐标系 ,请同学们回顾一下: 对点P(x,y),当y=0、y>0 、y<0时,点P位于坐标平面内什么位置?
①当y=0时:
②当y>0时:
y
x
1
2
3
4
5
-1
-2
-3
-4
-5
2
3
4
5
1
-1
-2
-3
-4
-5
o
y>0
y<0
点P在x轴上;
点P在x轴上方;
点P在x轴下方.
③当y<0时:
学习目标
认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系,会用函数观点解释方程和不等式及其解(解集)的意义。
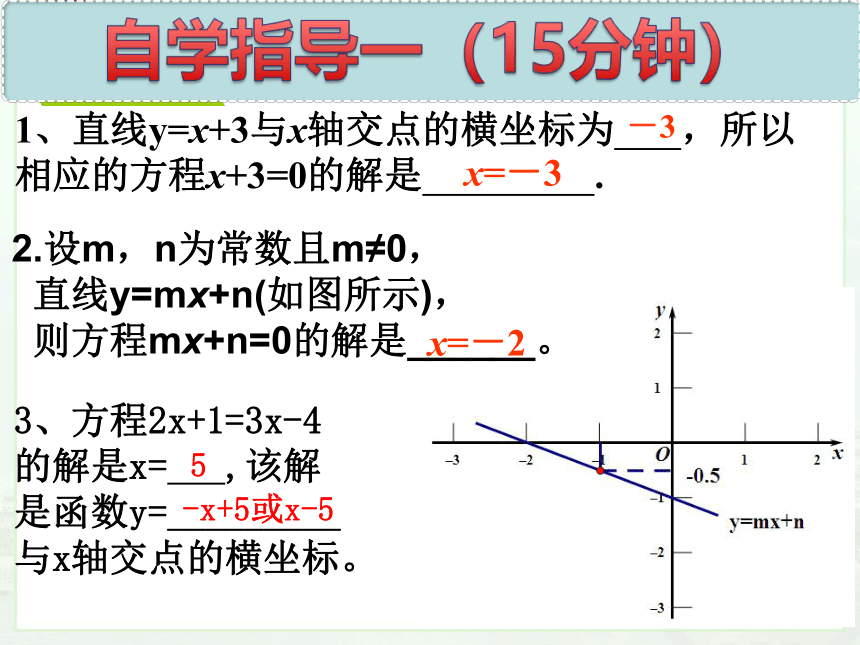
1、直线y=x+3与x轴交点的横坐标为 ,所以相应的方程x+3=0的解是 .
x=-3
-3
x=-2
2.设m,n为常数且m≠0,
直线y=mx+n(如图所示),
则方程mx+n=0的解是______。
3、方程2x+1=3x-4
的解是x= ,该解
是函数y=_________
与x轴交点的横坐标。
-x+5或x-5
5
自学指导一(15分钟)
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
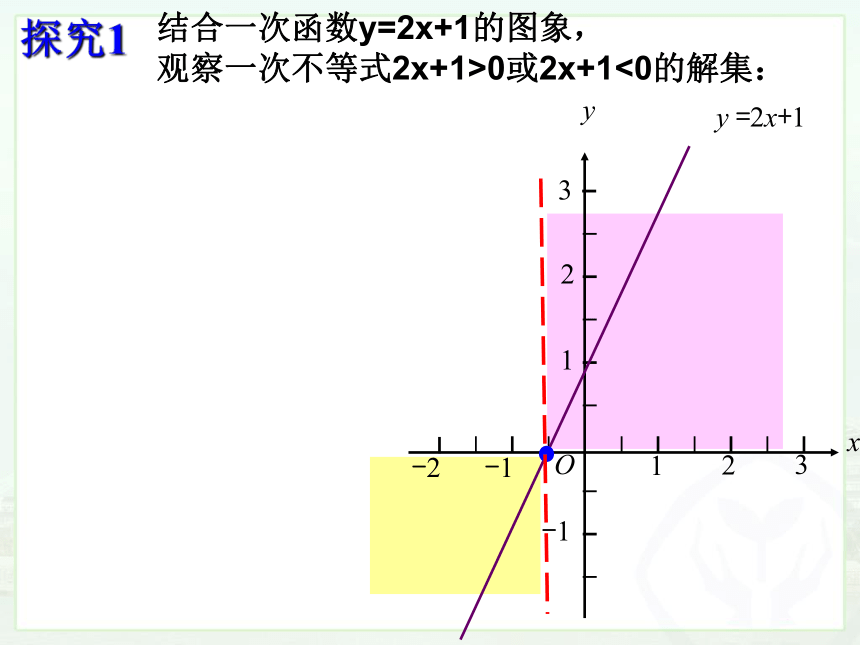
探究1
结合一次函数y=2x+1的图象,
观察一次不等式2x+1>0或2x+1<0的解集:
一次不等式与一次函数的关系
从“数”的角度看:
从“形”的角度看:
上方(下方)
求ax+b>0(<0)的解集
函数y=ax+b,当y 时,求 的取值范围;
求ax+b>0(<0)的解集
确定直线y=ax+b在x轴 的自变量x的取值范围;
>0(<0)
x
自学检测一(5分钟)
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
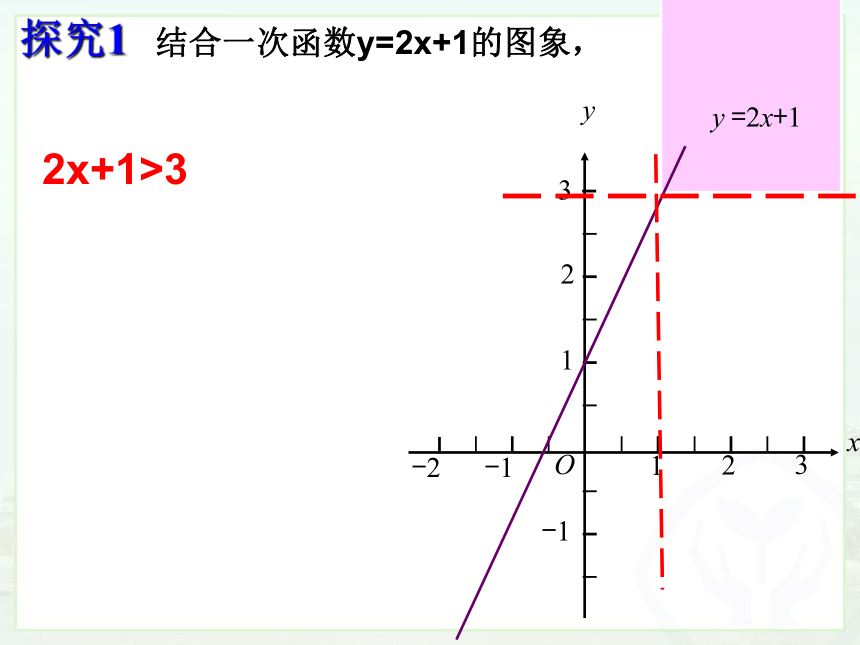
探究1
结合一次函数y=2x+1的图象,
2x+1>3
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
探究2
结合一次函数y=2x+1的图象
2x+1<-1
.一次函数 y=kx+b 的图象如图所示,你能说出 kx+b<0 的解集吗?
O
x
y
y=kx+b
-4
解集是 x< -4.
例题:用画函数图象的方法
解不等式5x+4<2x+10
解法1:原不等式化为:3x -6<0,
画出直线 y = 3x -6 (如图)
即这时y = 3x -6 <0
所以不等式的解集为:x<2
x<2
解法二:
画出函数 y 1= 5x+4和y 2=2x+10图象
从图中看出:
即直线 y 1= 5x +4 在 y 2= 2x +10
的___方
不等式5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10
的解集是x < 2
x < 2
下
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.
与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
1、请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
2、什么时刻,1号气球与2号气球
位于同一高度?位于什么高度?
自学指导二(5分钟)
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
(2)什么时刻,1 号气球与2 号气球位于同一高度? 位于什么高度?
总结:
一般地,每个二元一次方程组都对应着两个一次函数,于是也对应两条_____.
从“数”的角度看:
解方程组就相当于考虑自变量为何值时两个______的值相等;
从“形”的角度看:
解方程组就相当于确定两条直线的________。
二元一次方程组与一次函数的关系
直线
函数
交点坐标
用图象法解方程组:
2x+y=4
2x-3y=12
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3 - 4
自学检测二(5分钟)
本节课你有哪些收获?
课堂小结(2分钟)
作出函数y=3x-9的图象,并结合图象回答:
1.方程3x-9=0的解.
2.不等式3x-9≤0的解集 .
3.当3x-9>3时,求x的取值范围.
x
y
O
y=3x-9
(0,9)
(3,0)
练一练
当堂训练(5分钟)
19.2.3 一次函数与方程、不等式
第2课时
知识回顾
我们学面直角坐标系 ,请同学们回顾一下: 对点P(x,y),当y=0、y>0 、y<0时,点P位于坐标平面内什么位置?
①当y=0时:
②当y>0时:
y
x
1
2
3
4
5
-1
-2
-3
-4
-5
2
3
4
5
1
-1
-2
-3
-4
-5
o
y>0
y<0
点P在x轴上;
点P在x轴上方;
点P在x轴下方.
③当y<0时:
学习目标
认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系,会用函数观点解释方程和不等式及其解(解集)的意义。
1、直线y=x+3与x轴交点的横坐标为 ,所以相应的方程x+3=0的解是 .
x=-3
-3
x=-2
2.设m,n为常数且m≠0,
直线y=mx+n(如图所示),
则方程mx+n=0的解是______。
3、方程2x+1=3x-4
的解是x= ,该解
是函数y=_________
与x轴交点的横坐标。
-x+5或x-5
5
自学指导一(15分钟)
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
探究1
结合一次函数y=2x+1的图象,
观察一次不等式2x+1>0或2x+1<0的解集:
一次不等式与一次函数的关系
从“数”的角度看:
从“形”的角度看:
上方(下方)
求ax+b>0(<0)的解集
函数y=ax+b,当y 时,求 的取值范围;
求ax+b>0(<0)的解集
确定直线y=ax+b在x轴 的自变量x的取值范围;
>0(<0)
x
自学检测一(5分钟)
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
探究1
结合一次函数y=2x+1的图象,
2x+1>3
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
探究2
结合一次函数y=2x+1的图象
2x+1<-1
.一次函数 y=kx+b 的图象如图所示,你能说出 kx+b<0 的解集吗?
O
x
y
y=kx+b
-4
解集是 x< -4.
例题:用画函数图象的方法
解不等式5x+4<2x+10
解法1:原不等式化为:3x -6<0,
画出直线 y = 3x -6 (如图)
即这时y = 3x -6 <0
所以不等式的解集为:x<2
x<2
解法二:
画出函数 y 1= 5x+4和y 2=2x+10图象
从图中看出:
即直线 y 1= 5x +4 在 y 2= 2x +10
的___方
不等式5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10
的解集是x < 2
x < 2
下
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.
与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
1、请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
2、什么时刻,1号气球与2号气球
位于同一高度?位于什么高度?
自学指导二(5分钟)
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
(2)什么时刻,1 号气球与2 号气球位于同一高度? 位于什么高度?
总结:
一般地,每个二元一次方程组都对应着两个一次函数,于是也对应两条_____.
从“数”的角度看:
解方程组就相当于考虑自变量为何值时两个______的值相等;
从“形”的角度看:
解方程组就相当于确定两条直线的________。
二元一次方程组与一次函数的关系
直线
函数
交点坐标
用图象法解方程组:
2x+y=4
2x-3y=12
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3 - 4
自学检测二(5分钟)
本节课你有哪些收获?
课堂小结(2分钟)
作出函数y=3x-9的图象,并结合图象回答:
1.方程3x-9=0的解.
2.不等式3x-9≤0的解集 .
3.当3x-9>3时,求x的取值范围.
x
y
O
y=3x-9
(0,9)
(3,0)
练一练
当堂训练(5分钟)
