2021—2022学年人教版数学八年级下册19.3课题选择 选择方案 课件(共21张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.3课题选择 选择方案 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
19.3 课题学习
选择方案
学习目标(1分钟)
1、分析怎样选取上网收费方式;
2、分析如何租车比较便宜。
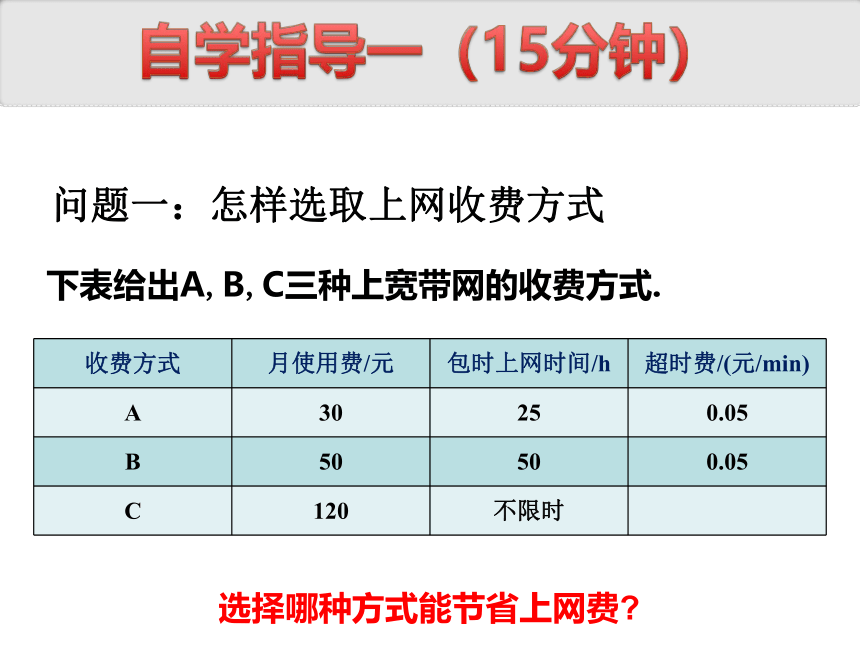
问题一:怎样选取上网收费方式
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种方式能节省上网费
下表给出A,B,C三种上宽带网的收费方式.
自学指导一(15分钟)
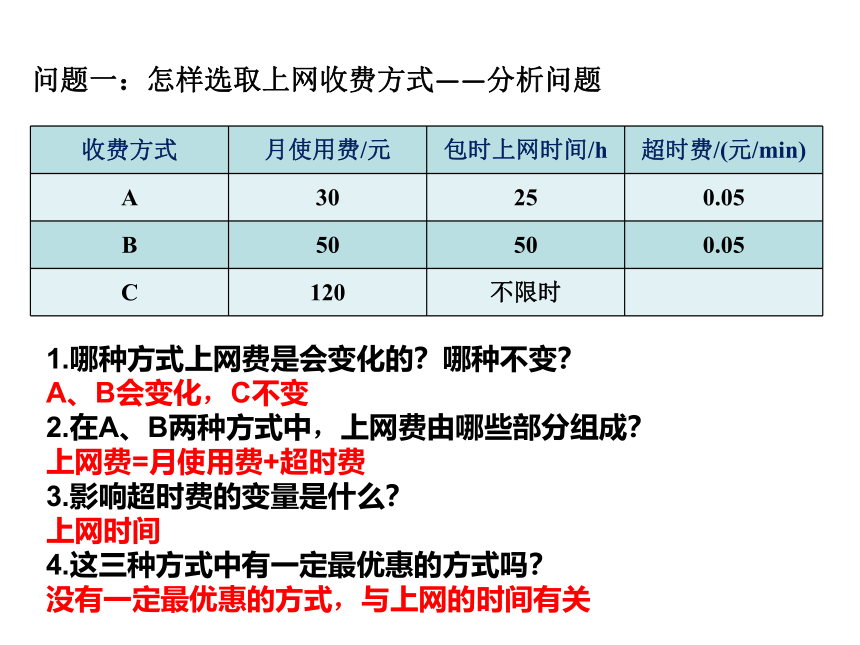
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
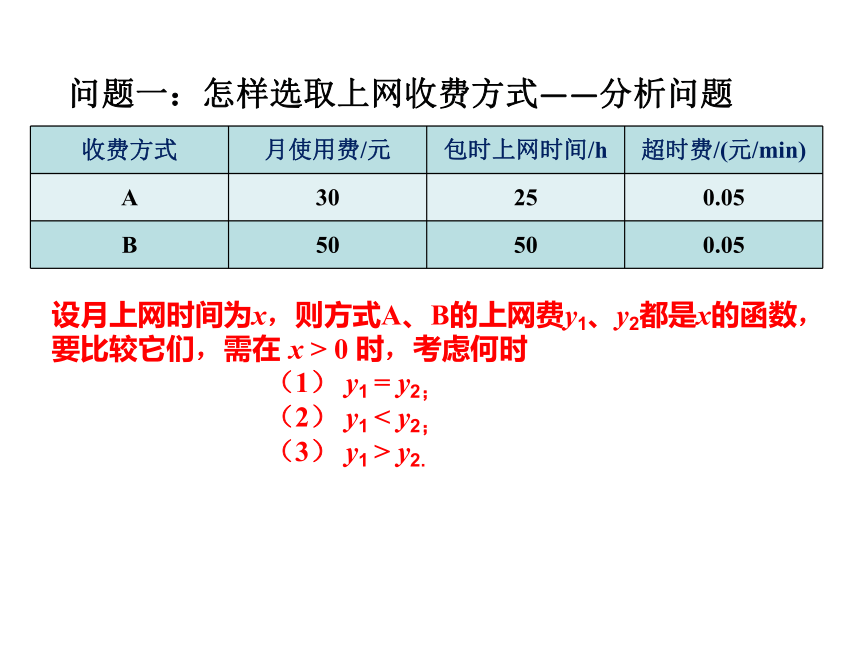
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
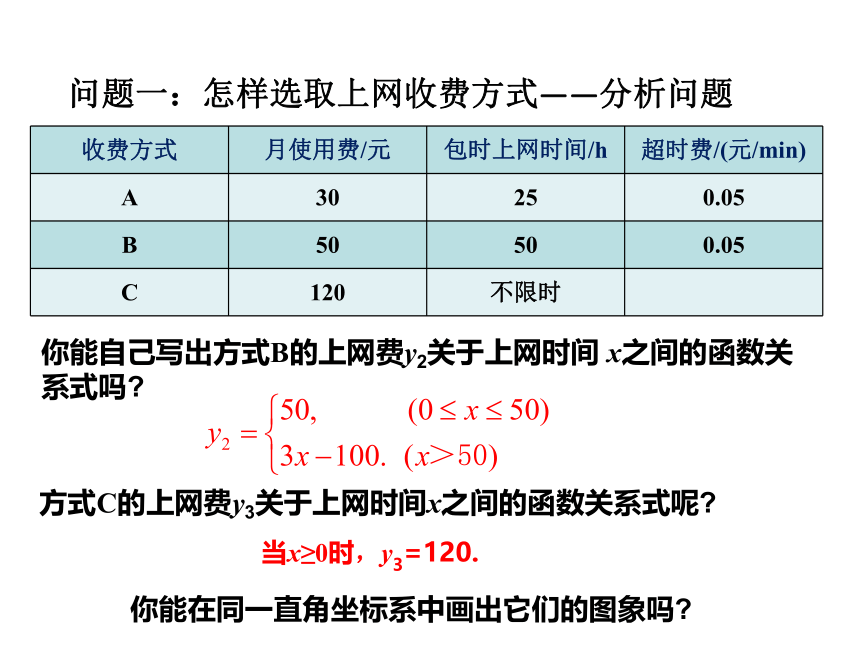
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
你能在同一直角坐标系中画出它们的图象吗
当x≥0时,y3=120.
问题一:怎样选取上网收费方式——解决问题
当上网时间__________时,
选择方式A最省钱.
当上网时间__________时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
怎样租车
某学校计划在总费用2300元的限额内,利用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师。现有甲、乙两种大客车,它们的载客量和租金如表 :
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
自学指导二(10分钟)
问题二:怎样租车——分析问题
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示 :
问题1:租车的方案有哪几种?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示 :
问题二:怎样租车——分析问题
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
说明了车辆总数不会超过6辆,可以排除方案2——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
x 辆
(6-x)辆
分析
(1)要保证240名师生有车坐
(2)要使每辆汽车上至少要有1名教师
根据(1)可知,汽车总数不能小于___;根据(2)可知,汽车总数不能大于___。综合起来可知汽车总数为 ___。
设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
问题
6
6
6
y=400x+280(6-x)
化简为: y=120x+1680
讨论
根据问题中的条件,自变量x 的取值应有几种能?
为使240名师生有车坐,x不能 小于_;为使租车费用不超过2300元,X不能超过_。综合起来可知x 的取值为__ 。
4
5
4、5
45x+30(6-x) ≥240
15x≥60
x≥4
400x+280(6-x) ≤2300
120x≤620
x≤31/6
∴4≤x≤31/6
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元。
方案一
方案二
在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由。
y=120x+1680
1000
2000
500
1500
1000
2000
2500
x(km)
y(元)
0
y1
y2
1.某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同. 设汽车每月行驶 x km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2 元,y1,y2 分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,租国有的合算.
当x=1500时,租两家的费用一样.
租个体车主的车合算.
自学检测二(10分钟)
变式练习
2.某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,分别计算两家旅行社的收费(建立表达式);
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x = 4时,两家旅行社的收费一样.
当x < 4时,甲旅行社优惠;当x > 4时,乙旅行社优惠.
课堂小结(1分钟)
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
甲 乙 丙
每辆汽车能装的吨数 2 1 1.5
每吨蔬菜可获利润(元) 500 700 400
1.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润 最大利润是多少
2.请你们结合日常生活中购物或通电话的实际问题,利用所学数学知识进行分析,选择最佳方案,并写出有关活动的报告.
当堂训练(5分钟)
19.3 课题学习
选择方案
学习目标(1分钟)
1、分析怎样选取上网收费方式;
2、分析如何租车比较便宜。
问题一:怎样选取上网收费方式
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种方式能节省上网费
下表给出A,B,C三种上宽带网的收费方式.
自学指导一(15分钟)
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
你能在同一直角坐标系中画出它们的图象吗
当x≥0时,y3=120.
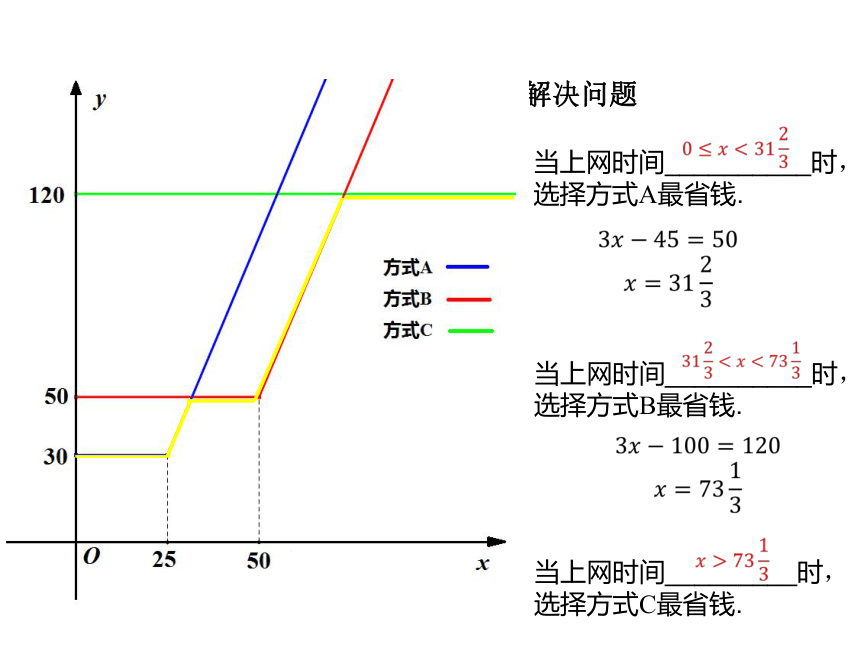
问题一:怎样选取上网收费方式——解决问题
当上网时间__________时,
选择方式A最省钱.
当上网时间__________时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
怎样租车
某学校计划在总费用2300元的限额内,利用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师。现有甲、乙两种大客车,它们的载客量和租金如表 :
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
自学指导二(10分钟)
问题二:怎样租车——分析问题
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示 :
问题1:租车的方案有哪几种?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示 :
问题二:怎样租车——分析问题
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
说明了车辆总数不会超过6辆,可以排除方案2——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
问题二:怎样租车——分析问题
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
x 辆
(6-x)辆
分析
(1)要保证240名师生有车坐
(2)要使每辆汽车上至少要有1名教师
根据(1)可知,汽车总数不能小于___;根据(2)可知,汽车总数不能大于___。综合起来可知汽车总数为 ___。
设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
问题
6
6
6
y=400x+280(6-x)
化简为: y=120x+1680
讨论
根据问题中的条件,自变量x 的取值应有几种能?
为使240名师生有车坐,x不能 小于_;为使租车费用不超过2300元,X不能超过_。综合起来可知x 的取值为__ 。
4
5
4、5
45x+30(6-x) ≥240
15x≥60
x≥4
400x+280(6-x) ≤2300
120x≤620
x≤31/6
∴4≤x≤31/6
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元。
方案一
方案二
在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由。
y=120x+1680
1000
2000
500
1500
1000
2000
2500
x(km)
y(元)
0
y1
y2
1.某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同. 设汽车每月行驶 x km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2 元,y1,y2 分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,租国有的合算.
当x=1500时,租两家的费用一样.
租个体车主的车合算.
自学检测二(10分钟)
变式练习
2.某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,分别计算两家旅行社的收费(建立表达式);
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x = 4时,两家旅行社的收费一样.
当x < 4时,甲旅行社优惠;当x > 4时,乙旅行社优惠.
课堂小结(1分钟)
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
甲 乙 丙
每辆汽车能装的吨数 2 1 1.5
每吨蔬菜可获利润(元) 500 700 400
1.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润 最大利润是多少
2.请你们结合日常生活中购物或通电话的实际问题,利用所学数学知识进行分析,选择最佳方案,并写出有关活动的报告.
当堂训练(5分钟)
