2021-2022学年人教版数学八年级下册20.1.1平均数 课件(共26张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册20.1.1平均数 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 762.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:48:10 | ||
图片预览




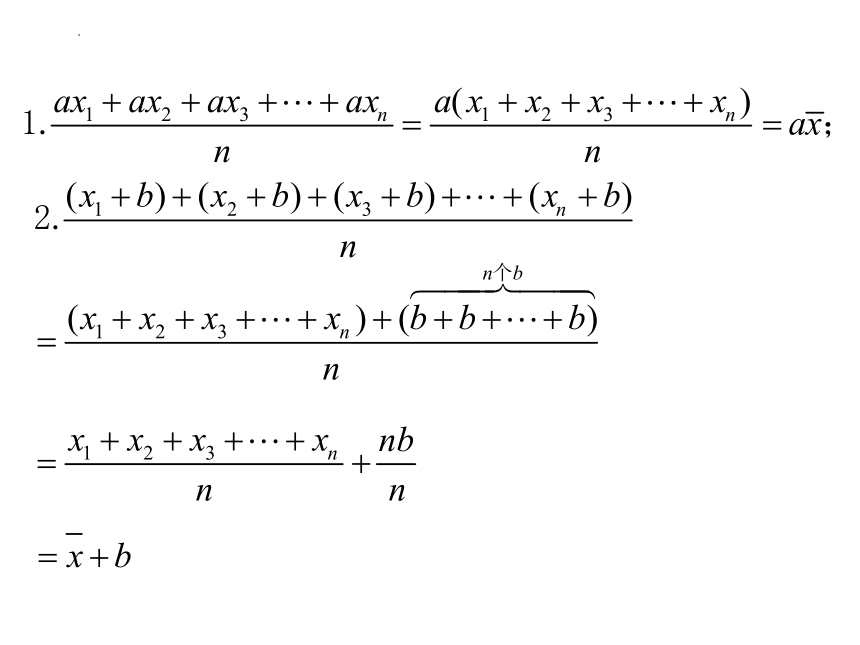
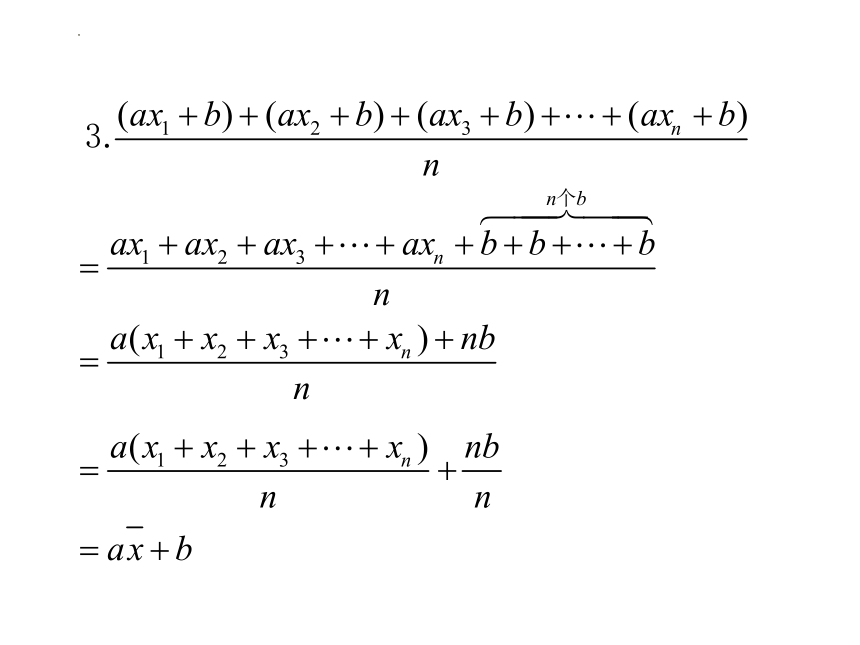


文档简介
(共26张PPT)
20.1.1 平均数
第二十章 数据的分析
教 学 目 标 知识技能 在平均数基础上进一步发展加权平均数的有关知识,并能运用 解决相关问题
过程与方法 通过独立思考自主探究等活动,进一步形成统计学知识与技能
情感态度价值观 在解决实际问题中,形成科学认识事物态度。
重点 运用 解决问题。
难点 “权”与“组中值”的确定
学习目标(1分钟)
自学指导一(5分钟)
算术平均数的定义:
对于n个数据x1, x2, x3,…, xn,则
叫做这n个数的算术平均数,简称平均数,
记为
读作“ 拔 ”
第1课时 算术平均数与加权平均数
1.5与11的平均数是____.
2.4与____的平均数是10.
3.求10个数的平均数,应先求出这10个数的____,再_________.
8
16
和
除以10
自学检测一(5分钟)
4a
4a-2
2、已知数据 的平均数为a, 则数据
的平均数为 ;
的平均数为
3、如果两组数据 和 的平均数分别为a和b,求一组新数据 的平均数.
1、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,
2a3+1 的平均数是( )
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
C
自学指导二(5分钟)
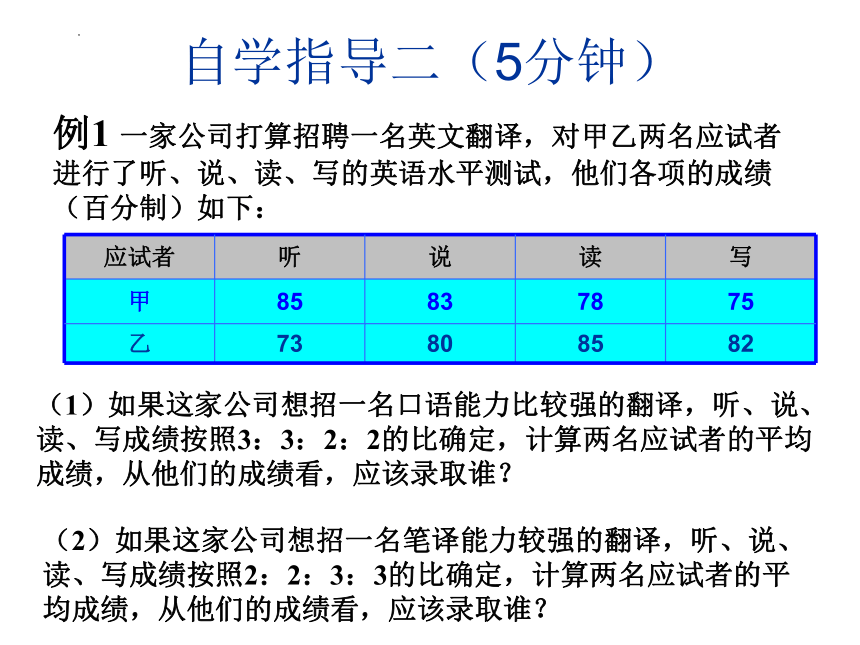
例1 一家公司打算招聘一名英文翻译,对甲乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力比较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
解:(1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲。
(2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为
乙的平均成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙。
加权平均数的定义:
若n个数据x1, x2, x3,…,xn
的权分别是ω1, ω2, ω3 ,…,ωn,
则
叫做这n个数的加权平均数。
数据的权能够反映的数据的相对“重要程度”。
1、下表是校女子排球队队员的年龄分布:
年龄 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄。
平均年龄=队员年龄总数/队员总人数
解: 13×1+14×4+15×5+16×2
1+4+5+2
≈15(岁)
题目中13岁出现了1次,1叫做13的权,14岁出现了 次, 是14的权,15岁出现了 次,
是15的权,16岁出现了 次, 是16的权。
分析
4
5
2
4
5
2
自学检测二(15分钟)
统计中也常把下面的这种算术平均数看成加权平均数。
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权。
归纳
2、为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
载客量/人
组中值
频数(班次)
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
讲授新课
说明 根据频数分布表求加权平均数时,统计中
常用各组的组中值代表各组的实际数据,把各组的频数
看作相应组中值的权.
根据上面的频数分布表求加权平均数时,统计中常用的各组的组中值代表各组的实际数据,把各组频数看作相应组中值的权。例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3,由此这天5路公共汽车平均每班的载客量是:
讲授新课
3、乐乐在本次考试中,语文101分,数学116分,英语111分,道德90分,历史92分,地理87分,生物93分,其中地理和生物按满分20分的比例计入总成绩,请问小明本次考试的平均分为几分?
第1课时 算术平均数与加权平均数
(1) 比赛后,甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四项得分分别按10%,40%,20%,30%折算记入总分.根据猜测,求出甲的总分;
七巧板拼图 趣题巧解 数学应用 魔方复原
甲 66 89 86 68
乙 66 60 80 68
丙 66 80 90 68
4、某校举办八年级学生数学素养大赛.下表为甲、乙、丙三位同学的得分情况(单位:分).
解:由题意,得甲的总分为:66×10%+89×40%+86×20%+68×30%=79.8(分)
解:设趣题巧解所占的百分比为x,数学运用所占的百分比为y,由题意,得
∴甲的总分为:20+89×0.3+86×0.4=81.1>80,
∴甲能获一等奖.
(2) 本次大赛组委会最后决定,总分为80分以上(包括80分)的学生获一等奖. 现获悉乙、丙的总分分别是70分,80分,甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分. 问甲能否获得这次比赛一等奖?
七巧板拼图 趣题巧解 数学应用 魔方复原
甲 66 89 86 68
乙 66 60 80 68
丙 66 80 90 68
问题1:求加权平均数的公式是什么?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
若n个数
的权分别是
则:
叫做这n个数的加权平均数。
课堂小结(1分钟)
问题2:你如何理解加权平均数中的权的意思?
问题3:当要考察的对象很多或考察本身带有破坏性时,统计学中常常使用什么方法获得对总体认识?
数据的权能够反映的数据的相对“重要程度”。
常常用样本数据的代表意义来估计总体
例如:实际生活中经常用样本平均数估计总体平均数。
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
1.种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜。
答:这个新品种黄瓜平均每株结16.25根黄瓜。
解:
当堂训练(15分钟)
2、果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?每个梨的质量?
所以,平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10
棵梨树上梨的个数,得到以下数据:154,150,155,
155,159,150,152,155,153,157.你能估计出平均
每棵树的梨的个数吗?
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以,平均每个梨的质量约为0.42 kg.
讲授新课
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
思考 这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以,该果园中梨的总产量约为6 468 kg.
讲授新课
解:
∵4个小组的组中值分别为150、160、170、180,
∴该班学生的平均身高为:
3、某班40名学生身高情况如图,请计算该班学生的平均身高.
=165.5 (cm)
20.1.1 平均数
第二十章 数据的分析
教 学 目 标 知识技能 在平均数基础上进一步发展加权平均数的有关知识,并能运用 解决相关问题
过程与方法 通过独立思考自主探究等活动,进一步形成统计学知识与技能
情感态度价值观 在解决实际问题中,形成科学认识事物态度。
重点 运用 解决问题。
难点 “权”与“组中值”的确定
学习目标(1分钟)
自学指导一(5分钟)
算术平均数的定义:
对于n个数据x1, x2, x3,…, xn,则
叫做这n个数的算术平均数,简称平均数,
记为
读作“ 拔 ”
第1课时 算术平均数与加权平均数
1.5与11的平均数是____.
2.4与____的平均数是10.
3.求10个数的平均数,应先求出这10个数的____,再_________.
8
16
和
除以10
自学检测一(5分钟)
4a
4a-2
2、已知数据 的平均数为a, 则数据
的平均数为 ;
的平均数为
3、如果两组数据 和 的平均数分别为a和b,求一组新数据 的平均数.
1、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,
2a3+1 的平均数是( )
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
C
自学指导二(5分钟)
例1 一家公司打算招聘一名英文翻译,对甲乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力比较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
解:(1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲。
(2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为
乙的平均成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙。
加权平均数的定义:
若n个数据x1, x2, x3,…,xn
的权分别是ω1, ω2, ω3 ,…,ωn,
则
叫做这n个数的加权平均数。
数据的权能够反映的数据的相对“重要程度”。
1、下表是校女子排球队队员的年龄分布:
年龄 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄。
平均年龄=队员年龄总数/队员总人数
解: 13×1+14×4+15×5+16×2
1+4+5+2
≈15(岁)
题目中13岁出现了1次,1叫做13的权,14岁出现了 次, 是14的权,15岁出现了 次,
是15的权,16岁出现了 次, 是16的权。
分析
4
5
2
4
5
2
自学检测二(15分钟)
统计中也常把下面的这种算术平均数看成加权平均数。
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权。
归纳
2、为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少
载客量/人 频数(班次)
1≤x<21 3
21≤x<41 5
41≤x<61 20
61≤x<81 22
81≤x<101 18
101≤x<121 15
载客量/人
组中值
频数(班次)
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
讲授新课
说明 根据频数分布表求加权平均数时,统计中
常用各组的组中值代表各组的实际数据,把各组的频数
看作相应组中值的权.
根据上面的频数分布表求加权平均数时,统计中常用的各组的组中值代表各组的实际数据,把各组频数看作相应组中值的权。例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3,由此这天5路公共汽车平均每班的载客量是:
讲授新课
3、乐乐在本次考试中,语文101分,数学116分,英语111分,道德90分,历史92分,地理87分,生物93分,其中地理和生物按满分20分的比例计入总成绩,请问小明本次考试的平均分为几分?
第1课时 算术平均数与加权平均数
(1) 比赛后,甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四项得分分别按10%,40%,20%,30%折算记入总分.根据猜测,求出甲的总分;
七巧板拼图 趣题巧解 数学应用 魔方复原
甲 66 89 86 68
乙 66 60 80 68
丙 66 80 90 68
4、某校举办八年级学生数学素养大赛.下表为甲、乙、丙三位同学的得分情况(单位:分).
解:由题意,得甲的总分为:66×10%+89×40%+86×20%+68×30%=79.8(分)
解:设趣题巧解所占的百分比为x,数学运用所占的百分比为y,由题意,得
∴甲的总分为:20+89×0.3+86×0.4=81.1>80,
∴甲能获一等奖.
(2) 本次大赛组委会最后决定,总分为80分以上(包括80分)的学生获一等奖. 现获悉乙、丙的总分分别是70分,80分,甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分. 问甲能否获得这次比赛一等奖?
七巧板拼图 趣题巧解 数学应用 魔方复原
甲 66 89 86 68
乙 66 60 80 68
丙 66 80 90 68
问题1:求加权平均数的公式是什么?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
若n个数
的权分别是
则:
叫做这n个数的加权平均数。
课堂小结(1分钟)
问题2:你如何理解加权平均数中的权的意思?
问题3:当要考察的对象很多或考察本身带有破坏性时,统计学中常常使用什么方法获得对总体认识?
数据的权能够反映的数据的相对“重要程度”。
常常用样本数据的代表意义来估计总体
例如:实际生活中经常用样本平均数估计总体平均数。
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
1.种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜。
答:这个新品种黄瓜平均每株结16.25根黄瓜。
解:
当堂训练(15分钟)
2、果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?每个梨的质量?
所以,平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10
棵梨树上梨的个数,得到以下数据:154,150,155,
155,159,150,152,155,153,157.你能估计出平均
每棵树的梨的个数吗?
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以,平均每个梨的质量约为0.42 kg.
讲授新课
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
思考 这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以,该果园中梨的总产量约为6 468 kg.
讲授新课
解:
∵4个小组的组中值分别为150、160、170、180,
∴该班学生的平均身高为:
3、某班40名学生身高情况如图,请计算该班学生的平均身高.
=165.5 (cm)
