2021-2022学年人教版数学八年级下册20.2.1 方差 课件(共35张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册20.2.1 方差 课件(共35张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:49:24 | ||
图片预览









文档简介
(共35张PPT)
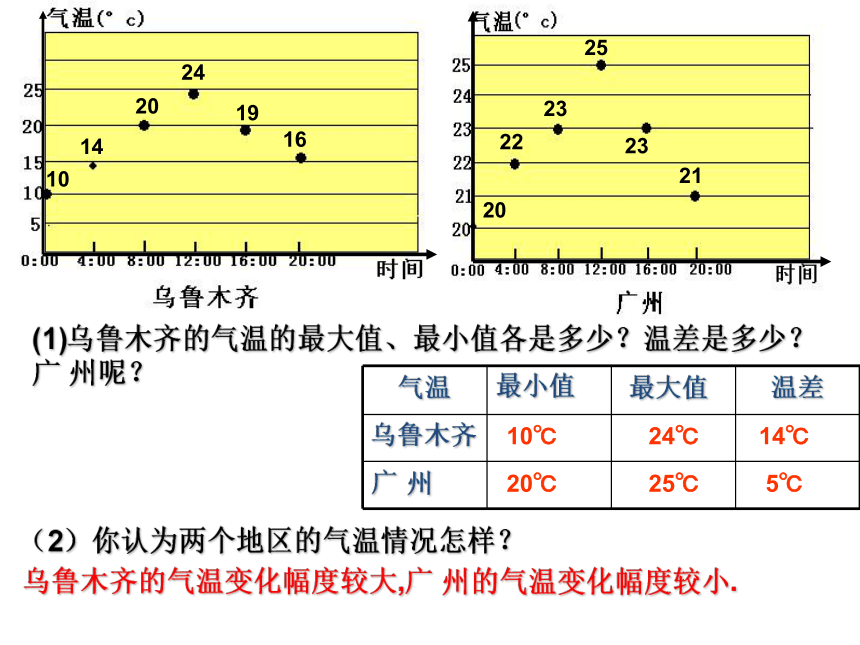
2.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90分
B.中位数是90分
C.平均数是90分
D.最大值与最小值的差是15分
C
1.__________、________和_________反映了一组数据的集中趋势.
平均数
众数
中位数
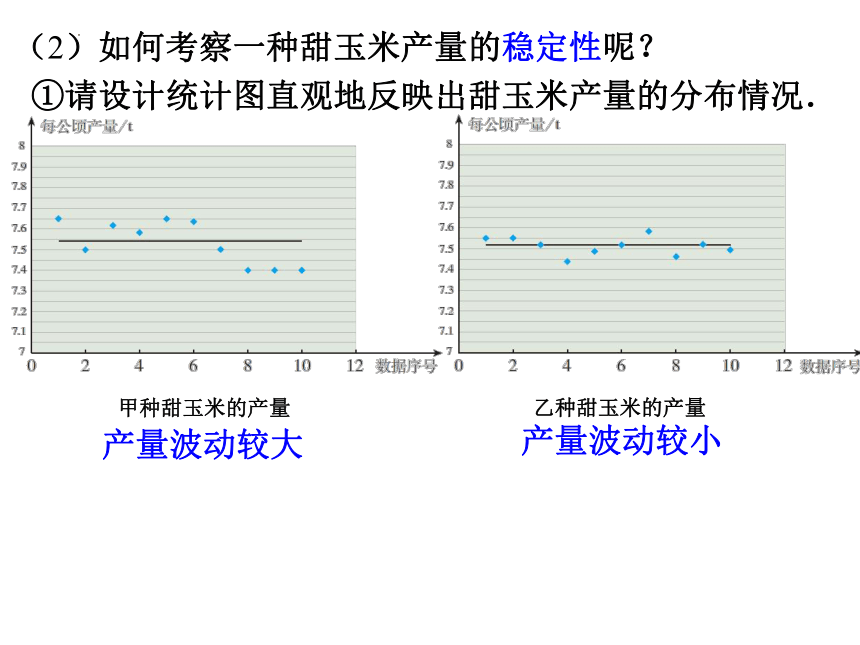
乌鲁木齐的气温变化幅度较大,广 州的气温变化幅度较小.
(1)乌鲁木齐的气温的最大值、最小值各是多少?温差是多少?广 州呢?
(2)你认为两个地区的气温情况怎样?
气温 最小值 最大值 温差
乌鲁木齐
广 州
14℃
10℃
24℃
5℃
20℃
25℃
14
24
19
16
20
10
22
23
25
23
21
20
最大值-最小值.
一组数据中的最大数据与最小数据的差
极差:
极差=
作用:极差能够反映数据的变化范围.
极差能够反映数据的变化范围,它是最简单的一种度量数据波动情况的量,但它受极端值的影响较大。也就是说,极差只能反映数据的波动范围,而不能具体反映所有数据的波动情况。
复习回顾
20.2 数据的波动程度
第一课时 方差
学习目标(1分钟)
(1)理解方差的定义,掌握方差的计算公式,并能熟练计算一组数据的方差;
(2)通过实例体会方差的实际意义.
自学指导一 (15分钟)
完成课本第124-125页的内容,找出方差的定义
以及计算公式,总结求方差的计算步骤,并理解方
差的实际意义。
问题1 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种
子呢?
说明在试验田中,甲、乙两种甜玉米的平均产量相
差不大.
可估计这个地区种植这两种甜玉米的平均产量相差
不大.
(1)上面两组数据的平均数
分别是:
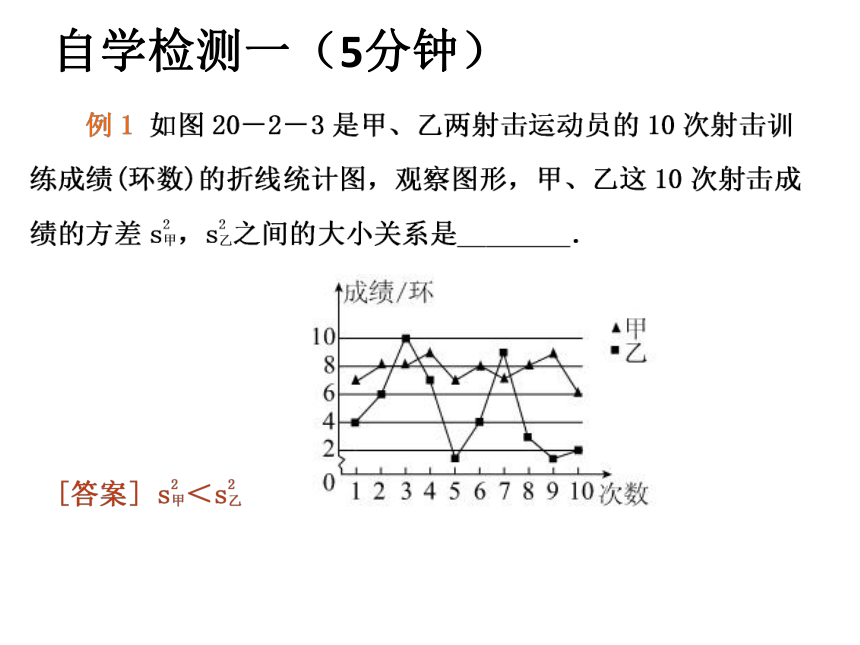
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲种甜玉米的产量
乙种甜玉米的产量
②统计学中常采用下面的做法来量化这组数据的波动大
小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
点拨运用(3分钟)
1、计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
2、运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
自学检测一(5分钟)
数据的单位与方差的单位一致吗?怎样解决
动动脑!
为了使单位一致,可用方差的算术平方根:
来表示,并把它叫做标准差(standardeviation).
方差=标准差的平方 标准差=方差的算术平方根
S=
1、在统计中,样本的方差和标准差可以近似的反映总体的( ).
A、平均状态
B、离散程度
C、分布规律
D、最大值和最小值
牛刀小试
B
自学指导二 (15分钟)
某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15 个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
解:样本数据的平均数分别是:
样本平均数相同,估计
这批鸡腿的平均质量相近.
样本数据的方差分别是:
由 可知,两家加工厂的鸡腿质量大致相等;
由 < 可知,甲加工厂的鸡腿质量更稳定,大小更均
匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
某篮球队对运动员进行3分球投篮成绩测试,
每人每天投3分球10次,对甲、乙两名队员在
五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 =8,
方差为 .
队员 每人每天进球数
甲 10 6 10 6 8
乙 7 9 7 8 9
( 1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
自学检测二(5分钟)
课堂小结 (1分钟)
课后小结
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
当堂训练 (10分钟)
1、样本方差的作用是( )
(A ) 表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、 在样本方差的计算公式
数字10 表示 ,数字20表示 .
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
4.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s2=29.6,s2=2.7,则关于两种小麦推广种植的合理决策是( )
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
D
5、一组数据按从小到大的顺序排列为1,2,3,x,4,5,
若这组数据的中位数为3,则这组数据的方差是
6、
7.
选做题:甲、乙、丙三名射击运动员在某场测试中各射击20次,三人的测试成绩如表1、表2、表3:
甲的成绩
环数 7 8 9 10
频数 4 6 6 4
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 5 5 5 5
试计算甲、乙、丙三名运动员测试成绩的方差,并确定成绩最稳定的是谁.
7.2 用坐标方法的简单应用
板书设计
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
对于数据3、2、1、0、-1
求:它的极差是————
方差是—————
标准差是—————
4
2
知识拓展
方差是0;
D、平均数是100,
差是0;
C、平均数是98,方
方差是2;
B、平均数是100,
差是2;
A、平均数是98,方
)
下列结论正确的是(
x
,
,
x
,
x
,
x
差为2,则对于样本
的平均数为100,方
2
x
2,
2,
x
2,
若样本x
n
3
2
1
n
3
2
1
+
+
+
+
A
思考:
x
…
…
,
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
你能用所发现的结论来解决以下的问题:
自学检测一(5分钟)
1、已知一组数据-2,-1,0,x,1的平均数是 0,那么这组数据的方差是 .
2
2、若一组数据2,3,4,5,x的方差与另一组数据5,6,
7,8,9的方差相等,则x的值为( )
A.1 B.6 C.1或6 D.5或6
C
变式1:已知一组数据x1,x2,…,xn的方差是s2,则新的
一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的
方差是____.(用含a,s2的代数式表示)
a2s2
2.(2016·广安)初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖:
那么被遮盖的两个数据依次是( )
A.35,2 B.36,4
C.35,3 D.36,3
编号 1 2 3 4 5 方差 平均成绩
得分 38 34 ■ 37 40 ■ 37
B
3.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
A.平均数是8.625
B.中位数为8
C.众数是8
D.锻炼时间超过8小时的有21人
B
2.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90分
B.中位数是90分
C.平均数是90分
D.最大值与最小值的差是15分
C
1.__________、________和_________反映了一组数据的集中趋势.
平均数
众数
中位数
乌鲁木齐的气温变化幅度较大,广 州的气温变化幅度较小.
(1)乌鲁木齐的气温的最大值、最小值各是多少?温差是多少?广 州呢?
(2)你认为两个地区的气温情况怎样?
气温 最小值 最大值 温差
乌鲁木齐
广 州
14℃
10℃
24℃
5℃
20℃
25℃
14
24
19
16
20
10
22
23
25
23
21
20
最大值-最小值.
一组数据中的最大数据与最小数据的差
极差:
极差=
作用:极差能够反映数据的变化范围.
极差能够反映数据的变化范围,它是最简单的一种度量数据波动情况的量,但它受极端值的影响较大。也就是说,极差只能反映数据的波动范围,而不能具体反映所有数据的波动情况。
复习回顾
20.2 数据的波动程度
第一课时 方差
学习目标(1分钟)
(1)理解方差的定义,掌握方差的计算公式,并能熟练计算一组数据的方差;
(2)通过实例体会方差的实际意义.
自学指导一 (15分钟)
完成课本第124-125页的内容,找出方差的定义
以及计算公式,总结求方差的计算步骤,并理解方
差的实际意义。
问题1 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种
子呢?
说明在试验田中,甲、乙两种甜玉米的平均产量相
差不大.
可估计这个地区种植这两种甜玉米的平均产量相差
不大.
(1)上面两组数据的平均数
分别是:
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲种甜玉米的产量
乙种甜玉米的产量
②统计学中常采用下面的做法来量化这组数据的波动大
小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
点拨运用(3分钟)
1、计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
2、运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
自学检测一(5分钟)
数据的单位与方差的单位一致吗?怎样解决
动动脑!
为了使单位一致,可用方差的算术平方根:
来表示,并把它叫做标准差(standardeviation).
方差=标准差的平方 标准差=方差的算术平方根
S=
1、在统计中,样本的方差和标准差可以近似的反映总体的( ).
A、平均状态
B、离散程度
C、分布规律
D、最大值和最小值
牛刀小试
B
自学指导二 (15分钟)
某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15 个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
解:样本数据的平均数分别是:
样本平均数相同,估计
这批鸡腿的平均质量相近.
样本数据的方差分别是:
由 可知,两家加工厂的鸡腿质量大致相等;
由 < 可知,甲加工厂的鸡腿质量更稳定,大小更均
匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
某篮球队对运动员进行3分球投篮成绩测试,
每人每天投3分球10次,对甲、乙两名队员在
五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 =8,
方差为 .
队员 每人每天进球数
甲 10 6 10 6 8
乙 7 9 7 8 9
( 1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
自学检测二(5分钟)
课堂小结 (1分钟)
课后小结
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
当堂训练 (10分钟)
1、样本方差的作用是( )
(A ) 表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、 在样本方差的计算公式
数字10 表示 ,数字20表示 .
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
4.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s2=29.6,s2=2.7,则关于两种小麦推广种植的合理决策是( )
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
D
5、一组数据按从小到大的顺序排列为1,2,3,x,4,5,
若这组数据的中位数为3,则这组数据的方差是
6、
7.
选做题:甲、乙、丙三名射击运动员在某场测试中各射击20次,三人的测试成绩如表1、表2、表3:
甲的成绩
环数 7 8 9 10
频数 4 6 6 4
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 5 5 5 5
试计算甲、乙、丙三名运动员测试成绩的方差,并确定成绩最稳定的是谁.
7.2 用坐标方法的简单应用
板书设计
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
对于数据3、2、1、0、-1
求:它的极差是————
方差是—————
标准差是—————
4
2
知识拓展
方差是0;
D、平均数是100,
差是0;
C、平均数是98,方
方差是2;
B、平均数是100,
差是2;
A、平均数是98,方
)
下列结论正确的是(
x
,
,
x
,
x
,
x
差为2,则对于样本
的平均数为100,方
2
x
2,
2,
x
2,
若样本x
n
3
2
1
n
3
2
1
+
+
+
+
A
思考:
x
…
…
,
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
你能用所发现的结论来解决以下的问题:
自学检测一(5分钟)
1、已知一组数据-2,-1,0,x,1的平均数是 0,那么这组数据的方差是 .
2
2、若一组数据2,3,4,5,x的方差与另一组数据5,6,
7,8,9的方差相等,则x的值为( )
A.1 B.6 C.1或6 D.5或6
C
变式1:已知一组数据x1,x2,…,xn的方差是s2,则新的
一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的
方差是____.(用含a,s2的代数式表示)
a2s2
2.(2016·广安)初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖:
那么被遮盖的两个数据依次是( )
A.35,2 B.36,4
C.35,3 D.36,3
编号 1 2 3 4 5 方差 平均成绩
得分 38 34 ■ 37 40 ■ 37
B
3.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
A.平均数是8.625
B.中位数为8
C.众数是8
D.锻炼时间超过8小时的有21人
B
