2021—2022学年人教版数学八年级下册第19章 一次函数—— 一次函数的应用专题课件(共15张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册第19章 一次函数—— 一次函数的应用专题课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 984.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:51:45 | ||
图片预览





文档简介
(共15张PPT)
一次函数的应用专题
学习目标(1分钟)
1、一次函数图像的平移问题
2、一次函数与面积问题
3、一次函数的最值问题
4、一次函数的实际应用
自学指导一 (5分钟)
1.直线y=2x向上平移5个单位长度,得直线______.
y=2x+5
2.函数y=2x-3的图象可以看作由函数y=2x+7的图象向________平移________个单位长度得到.
下 10
3.一次函数y=x-2的图象与两坐标轴围成的三角形的面积为________.
4.直线y=x,y=-x+2与x轴围成的三角形的面积为________.
2
1
自学检测一(5分钟)
1.直线y=x+3与x轴交于点A,与y轴交于点B,直线y=2x+1与x轴交于点C,与y轴交于点D,则四边形ACDB的面积是( )
A. B. C. D.
B
2.已知一条直线经过点A(0,2),B(1,0),将这条直线向左平移与x轴、y轴分别交于点C,D.若DB=DC,则直线CD的函数解析式为________.
y=-2x-2
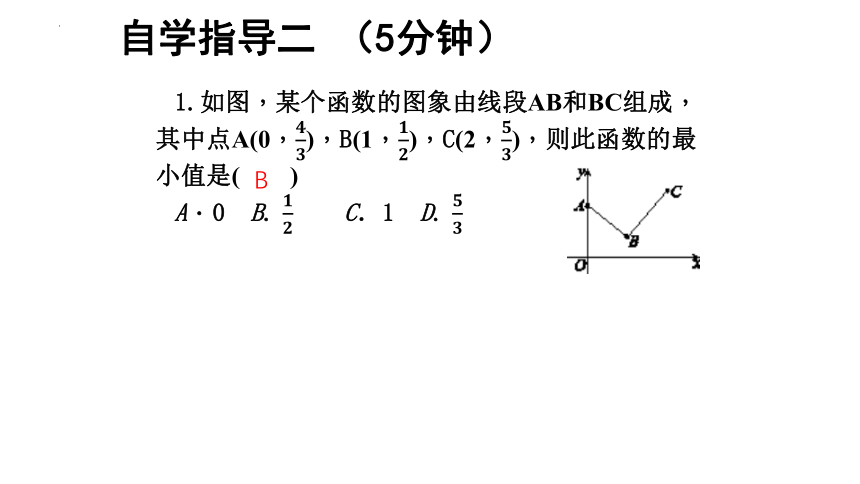
自学指导二 (5分钟)
1.如图,某个函数的图象由线段AB和BC组成,其中点A(0,),B(1,),C(2,),则此函数的最小值是( )
A.0 B. C.1 D.
B
2.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(kg)与上市时间x(天)的函数关系如图①所示,樱桃价格z(元/kg)与上市时间x(天)的函数关系如图②所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x之间的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多.
120
(2)日销售量y与上市时间x之间的函数解析式为:
当0≤x≤12, y=10x
当12<x≤20,y=-15x+300.
(3)由函数图象②可得,第10天和第12天均在第5天和第15天之间,当5<x≤15时,直线过(5,32),(15,12)两点.
设樱桃价格z与上市时间x之间的函数解析式为
z=mx+n.
15m+n=12.
5m+n=32,
所以z=-2x+42.
∴当x=10时,日销售量y=100,樱桃价格z=22, 销售金额为22×100=2200(元);
当x=12时,日销售量y=120,樱桃价格z=18,销售金额为18×120=2160(元).
自学检测二 (5分钟)
1、在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为________.
2、为庆祝商都正式营业,商都推出
了两种购物方案.
方案一:非会员购物所有商品价格
可获九五折优惠;方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱.
解:(1)方案一:y=0.95x;
方案二:y=0.9x+300.
(2)当x=5880时,
方案一:y=0.95x=5586;
方案二:y=0.9x+300=5592.
因为5586<5592,
所以选择方案一更省钱.
课堂小结 (1分钟)
1.用待定系数法求函数解析式的一般步骤.
2.数形结合解决问题的一般思路.
当堂训练 (10分钟)
1.如图所示,直线AB是一次函数y=kx+b
的图像,若AB= ,则一次函数的表
达式为 。
2.
3.
选做题
4.
一次函数的应用专题
学习目标(1分钟)
1、一次函数图像的平移问题
2、一次函数与面积问题
3、一次函数的最值问题
4、一次函数的实际应用
自学指导一 (5分钟)
1.直线y=2x向上平移5个单位长度,得直线______.
y=2x+5
2.函数y=2x-3的图象可以看作由函数y=2x+7的图象向________平移________个单位长度得到.
下 10
3.一次函数y=x-2的图象与两坐标轴围成的三角形的面积为________.
4.直线y=x,y=-x+2与x轴围成的三角形的面积为________.
2
1
自学检测一(5分钟)
1.直线y=x+3与x轴交于点A,与y轴交于点B,直线y=2x+1与x轴交于点C,与y轴交于点D,则四边形ACDB的面积是( )
A. B. C. D.
B
2.已知一条直线经过点A(0,2),B(1,0),将这条直线向左平移与x轴、y轴分别交于点C,D.若DB=DC,则直线CD的函数解析式为________.
y=-2x-2
自学指导二 (5分钟)
1.如图,某个函数的图象由线段AB和BC组成,其中点A(0,),B(1,),C(2,),则此函数的最小值是( )
A.0 B. C.1 D.
B
2.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(kg)与上市时间x(天)的函数关系如图①所示,樱桃价格z(元/kg)与上市时间x(天)的函数关系如图②所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x之间的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多.
120
(2)日销售量y与上市时间x之间的函数解析式为:
当0≤x≤12, y=10x
当12<x≤20,y=-15x+300.
(3)由函数图象②可得,第10天和第12天均在第5天和第15天之间,当5<x≤15时,直线过(5,32),(15,12)两点.
设樱桃价格z与上市时间x之间的函数解析式为
z=mx+n.
15m+n=12.
5m+n=32,
所以z=-2x+42.
∴当x=10时,日销售量y=100,樱桃价格z=22, 销售金额为22×100=2200(元);
当x=12时,日销售量y=120,樱桃价格z=18,销售金额为18×120=2160(元).
自学检测二 (5分钟)
1、在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为________.
2、为庆祝商都正式营业,商都推出
了两种购物方案.
方案一:非会员购物所有商品价格
可获九五折优惠;方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱.
解:(1)方案一:y=0.95x;
方案二:y=0.9x+300.
(2)当x=5880时,
方案一:y=0.95x=5586;
方案二:y=0.9x+300=5592.
因为5586<5592,
所以选择方案一更省钱.
课堂小结 (1分钟)
1.用待定系数法求函数解析式的一般步骤.
2.数形结合解决问题的一般思路.
当堂训练 (10分钟)
1.如图所示,直线AB是一次函数y=kx+b
的图像,若AB= ,则一次函数的表
达式为 。
2.
3.
选做题
4.
