2022-2023学年人教版七年级数学下册8.2.1代入消元法解二元一次方程组 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册8.2.1代入消元法解二元一次方程组 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 16:57:24 | ||
图片预览




文档简介
(共15张PPT)
8.2消元解二元一次方程组(1)
人教版数学七年级下册
第八章《二元一次方程组》
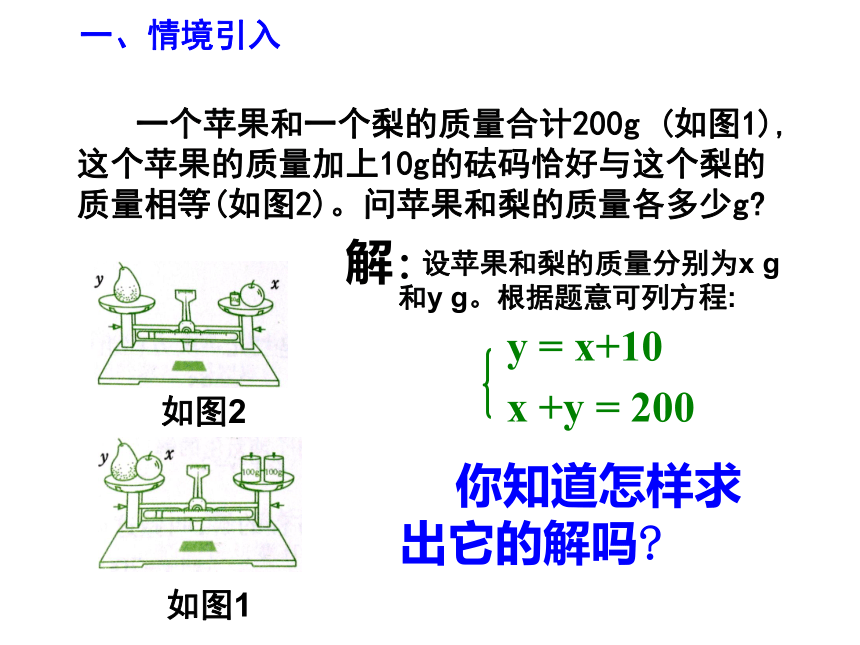
一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g
x +y = 200
y = x+10
你知道怎样求出它的解吗
解:
设苹果和梨的质量分别为x g 和y g。根据题意可列方程:
如图2
如图1
一、情境引入
x +y = 200
y = x+10
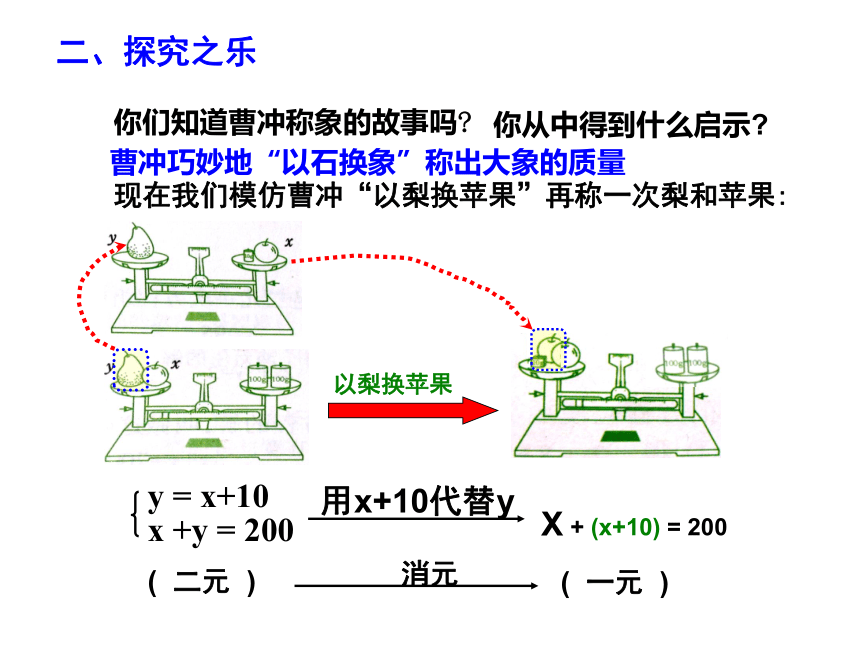
你们知道曹冲称象的故事吗
你从中得到什么启示
曹冲巧妙地“以石换象”称出大象的质量
现在我们模仿曹冲“以梨换苹果”再称一次梨和苹果:
用x+10代替y
X + (x+10) = 200
( 二元 )
( 一元 )
消元
以梨换苹果
二、探究之乐
.
x + y = 200
y = x+20
解方程组
②
①
y用含x的式子表示
我发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
思考:
具备什么特征的方程组可以直接代入消元?
.
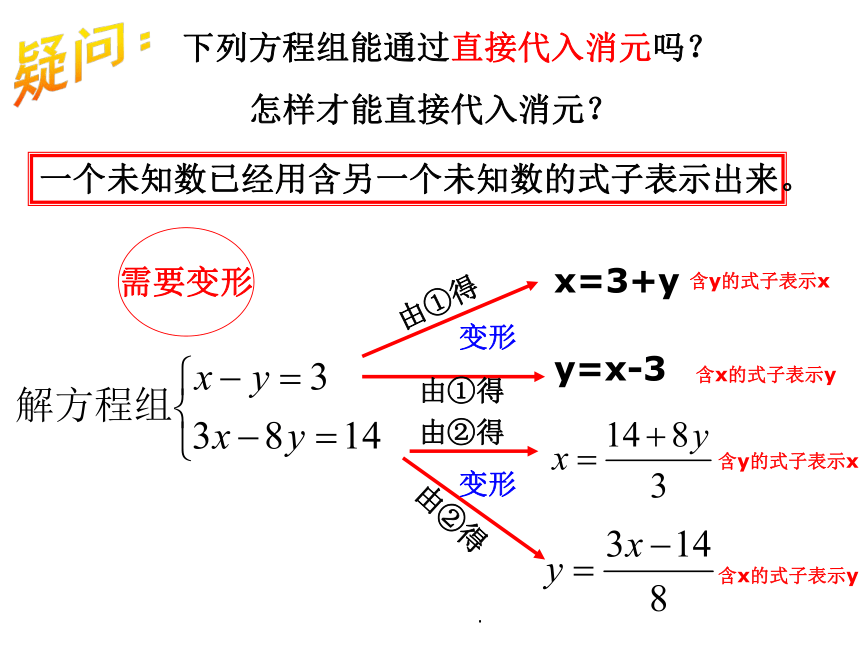
下列方程组能通过直接代入消元吗?
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
疑问:
需要变形
.
下列方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
变形
由①得
由①得
由②得
由②得
疑问:
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
.
例1 解方程组
x –y = 3
3x -8 y = 14
解:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
y = – 1
x=2
y = -1
∴这个方程组的解是
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
.
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
②
①
解:由②,得 ③
把③代入①,得
……
教室里,小明和小芳正在解方程组,此时:
小明
小芳
.
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
我发现:选择系数较简单的方程变形,把相应的未知数用含另一个未知数的式子表示出来,然后代入消元,可以简便计算。
②
①
.
抢答:为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
①
②
①
②
①
②
①
②
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
1.消元实质
2.代入法的一般步骤
3.能灵活运用适当方法解二元一次方程组
二元一次方程组
消 元
代入法
一元一次方程
即:
变形
代替
回代
写解
三、知识之谐
我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头
解:
设有笼中有鸡x只,有兔y只。则可列出方程组:
x + y = 35
2x + 4y = 94
四、文化之魅
五、德育之效
大家都熟悉曹冲称象的故事,把大象重量转化为石头的重量,以称出大象的重量。200多年前,幼小的曹冲就有这样惊人的智慧,怎么不叫人称赞。 这个故事,启发我们在现实生活中遇事多动脑筋,经常锻炼自己的思维能力,使人变得越来越聪明,同时也体现了数学中一种重要的思想方法---转化与化归。
对于某些数学问题,灵活运用整体思想,可以化难为易. 在解二元一次方程组时,可以运用整体代入法. 如解方程组
解:把②代入①,得x+2×1=3. 解得x=1.
把x=1代入②,得y=0.
所以方程组的解为
请用同样的方法解方程组
x+2(x+y)=3,①
x+y=1. ②
2x-y-2=0, ①
+2y=9. ②
x=1,
y=0.
六、巩固提高
解:由①,得2x-y=2. ③
把③代入②,得 +2y=9.
解得y=4.
把y=4代入③,得x=3.
∴方程组的解为
x=3,
y=4.
8.2消元解二元一次方程组(1)
人教版数学七年级下册
第八章《二元一次方程组》
一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g
x +y = 200
y = x+10
你知道怎样求出它的解吗
解:
设苹果和梨的质量分别为x g 和y g。根据题意可列方程:
如图2
如图1
一、情境引入
x +y = 200
y = x+10
你们知道曹冲称象的故事吗
你从中得到什么启示
曹冲巧妙地“以石换象”称出大象的质量
现在我们模仿曹冲“以梨换苹果”再称一次梨和苹果:
用x+10代替y
X + (x+10) = 200
( 二元 )
( 一元 )
消元
以梨换苹果
二、探究之乐
.
x + y = 200
y = x+20
解方程组
②
①
y用含x的式子表示
我发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
思考:
具备什么特征的方程组可以直接代入消元?
.
下列方程组能通过直接代入消元吗?
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
疑问:
需要变形
.
下列方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
变形
由①得
由①得
由②得
由②得
疑问:
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
.
例1 解方程组
x –y = 3
3x -8 y = 14
解:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
y = – 1
x=2
y = -1
∴这个方程组的解是
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
.
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
②
①
解:由②,得 ③
把③代入①,得
……
教室里,小明和小芳正在解方程组,此时:
小明
小芳
.
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
我发现:选择系数较简单的方程变形,把相应的未知数用含另一个未知数的式子表示出来,然后代入消元,可以简便计算。
②
①
.
抢答:为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
①
②
①
②
①
②
①
②
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
1.消元实质
2.代入法的一般步骤
3.能灵活运用适当方法解二元一次方程组
二元一次方程组
消 元
代入法
一元一次方程
即:
变形
代替
回代
写解
三、知识之谐
我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头
解:
设有笼中有鸡x只,有兔y只。则可列出方程组:
x + y = 35
2x + 4y = 94
四、文化之魅
五、德育之效
大家都熟悉曹冲称象的故事,把大象重量转化为石头的重量,以称出大象的重量。200多年前,幼小的曹冲就有这样惊人的智慧,怎么不叫人称赞。 这个故事,启发我们在现实生活中遇事多动脑筋,经常锻炼自己的思维能力,使人变得越来越聪明,同时也体现了数学中一种重要的思想方法---转化与化归。
对于某些数学问题,灵活运用整体思想,可以化难为易. 在解二元一次方程组时,可以运用整体代入法. 如解方程组
解:把②代入①,得x+2×1=3. 解得x=1.
把x=1代入②,得y=0.
所以方程组的解为
请用同样的方法解方程组
x+2(x+y)=3,①
x+y=1. ②
2x-y-2=0, ①
+2y=9. ②
x=1,
y=0.
六、巩固提高
解:由①,得2x-y=2. ③
把③代入②,得 +2y=9.
解得y=4.
把y=4代入③,得x=3.
∴方程组的解为
x=3,
y=4.
