北师大版九年级数学上册4.5相似三角形判定定理的证明同步练习(含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.5相似三角形判定定理的证明同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 950.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 18:55:39 | ||
图片预览

文档简介
北师大版九上 4.5 相似三角形判定定理的证明
一、选择题(共13小题)
1. 如图,点 ,,,,,,,, 都是 方格纸中的格点,为使 ,则点 应是 ,,, 四点中的
A. B. C. D.
2. 与 相交于 ,,, 是 上的点,, 是 上的点,且 ,,则图中与 相似的三角形(不含 )共有
A. 个 B. 个 C. 个 D. 个
3. 要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为 ,,,另一个三角形框架的一边长为 ,它的另外两边长分别可以为
A. , B. ,
C. , D. , 或 , 或 ,
4. 如图,在大小为 的正方形网格中,是相似三角形的是
A. ①和② B. ②和③ C. ①和③ D. ②和④
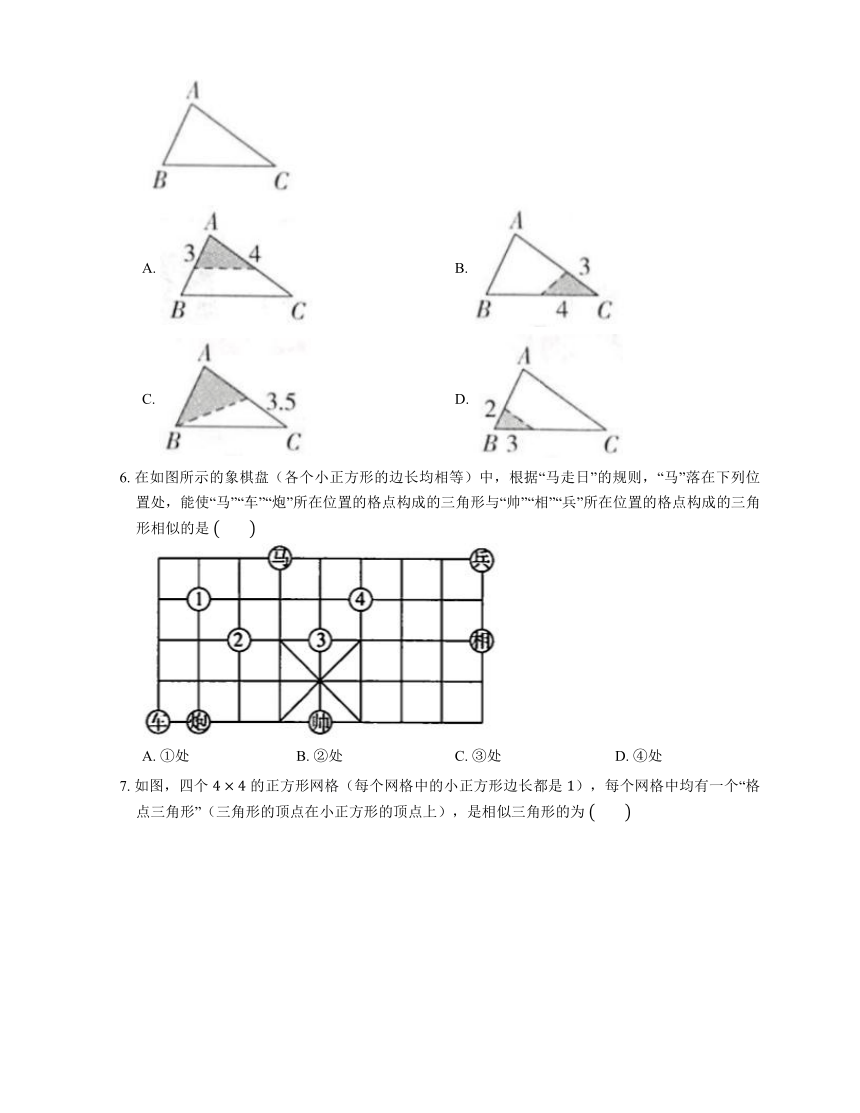
5. 如图,在 中,,,,将 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是
A. B.
C. D.
6. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”落在下列位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似的是
A. ①处 B. ②处 C. ③处 D. ④处
7. 如图,四个 的正方形网格(每个网格中的小正方形边长都是 ),每个网格中均有一个“格点三角形”(三角形的顶点在小正方形的顶点上),是相似三角形的为
A. ①③ B. ①② C. ②③ D. ②④
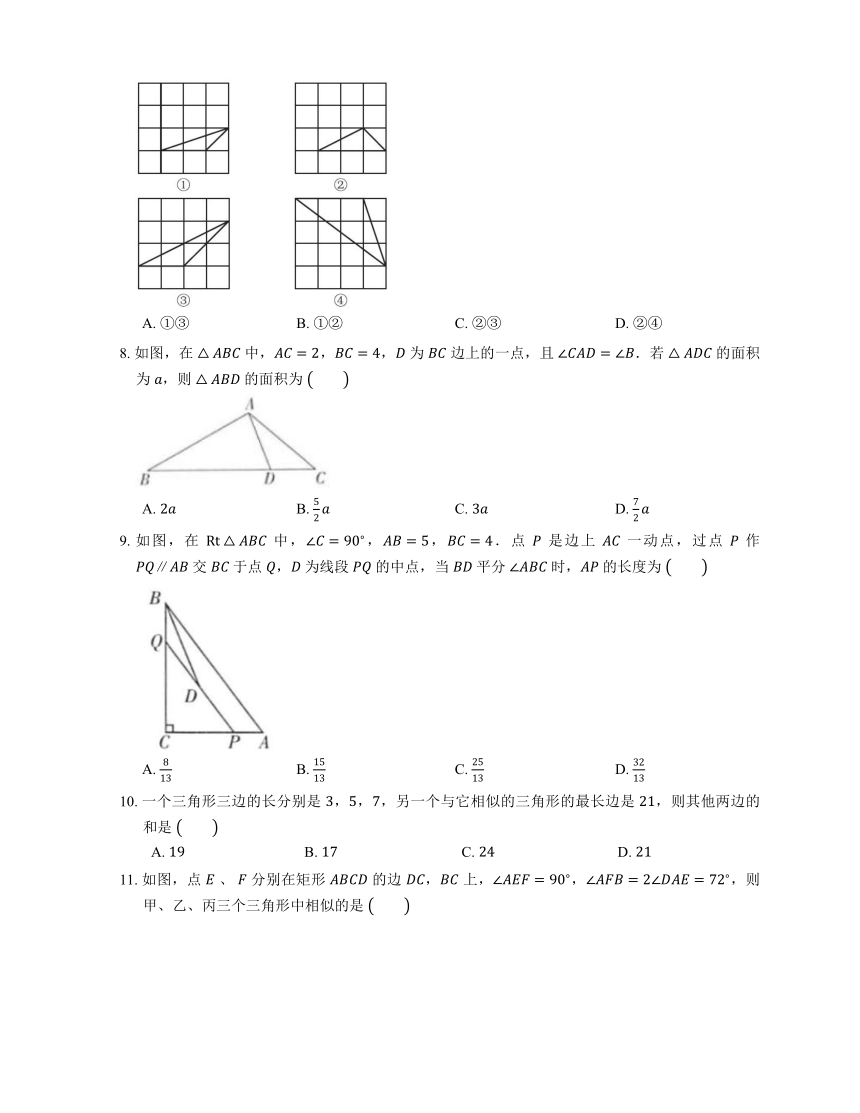
8. 如图,在 中,,, 为 边上的一点,且 .若 的面积为 ,则 的面积为
A. B. C. D.
9. 如图,在 中,,,.点 是边上 一动点,过点 作 交 于点 , 为线段 的中点,当 平分 时, 的长度为
A. B. C. D.
10. 一个三角形三边的长分别是 ,,,另一个与它相似的三角形的最长边是 ,则其他两边的和是
A. B. C. D.
11. 如图,点 、 分别在矩形 的边 , 上,,,则甲、乙、丙三个三角形中相似的是
A. 只有甲与乙 B. 只有乙与丙 C. 只有甲与丙 D. 甲与乙与丙
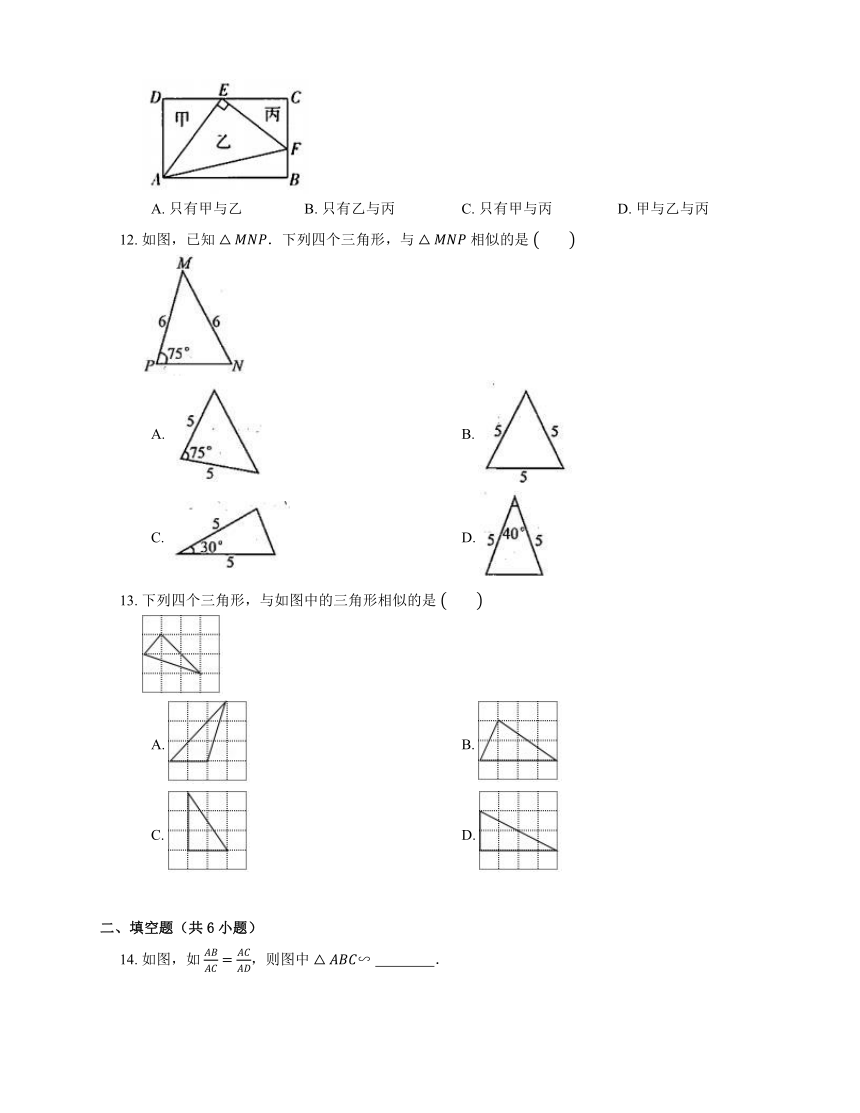
12. 如图,已知 .下列四个三角形,与 相似的是
A. B.
C. D.
13. 下列四个三角形,与如图中的三角形相似的是
A. B.
C. D.
二、填空题(共6小题)
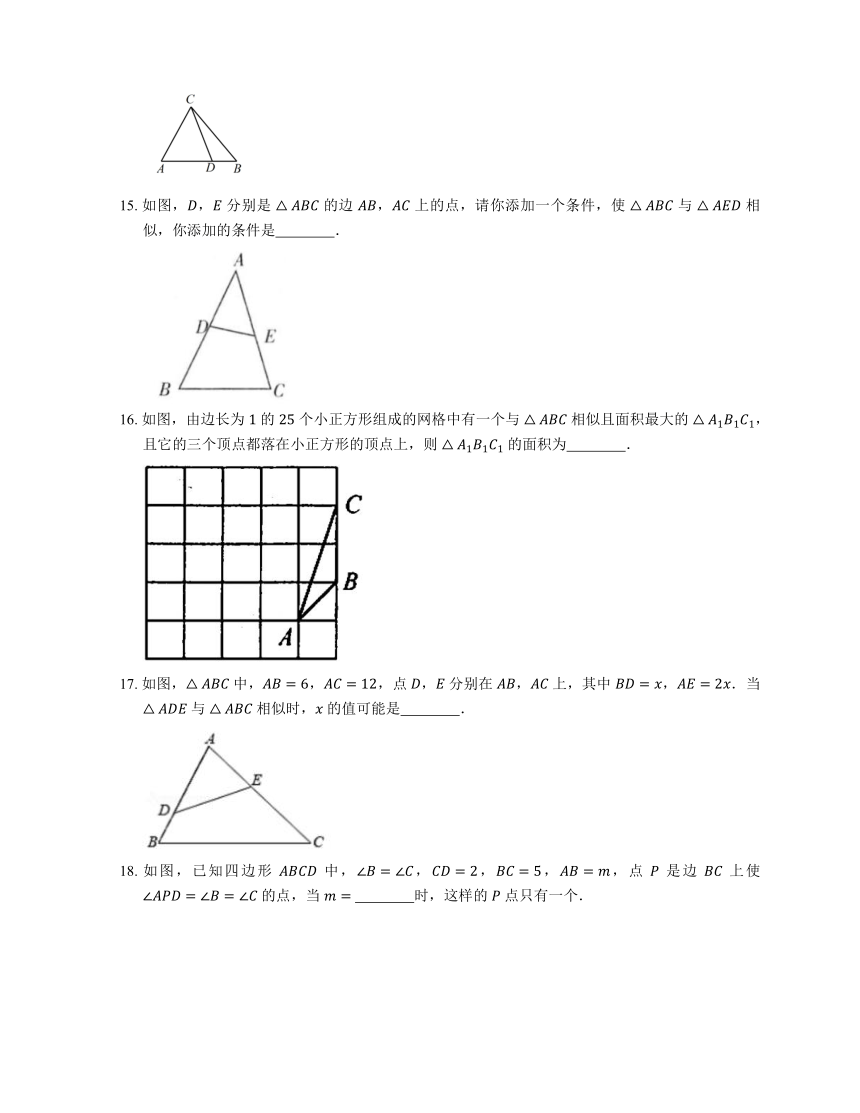
14. 如图,如 ,则图中 .
15. 如图,, 分别是 的边 , 上的点,请你添加一个条件,使 与 相似,你添加的条件是 .
16. 如图,由边长为 的 个小正方形组成的网格中有一个与 相似且面积最大的 ,且它的三个顶点都落在小正方形的顶点上,则 的面积为 .
17. 如图, 中,,,点 , 分别在 , 上,其中 ,.当 与 相似时, 的值可能是 .
18. 如图,已知四边形 中,,,,,点 是边 上使 的点,当 时,这样的 点只有一个.
19. 两个相似三角形的最短边分别是 和 ,它们的周长之差是 ,那么小三角形的周长为 .
三、解答题(共7小题)
20. 已知:在 中, 比 大 ,,求 与 的度数.
21. 如图,在 中,,,, 分别是 , 的平分线,且相交于点 ,写出与 相似的三角形.
22. 如图所示,在 中,,,点 从点 开始沿 边以 的速度向点 移动,点 从点 开始沿 边以 的速度向点 移动,如果 , 分别从 , 两点同时出发,经几秒后,以点 ,, 为顶点的三角形与 相似
23. 如图,在边长为 的 的正方形网格上有两个三角形,它们的顶点都在格点上, 与 是否相似 请说明理由.
24. 求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的 及线段 ,(),以线段 为一边,在给出的图形上用尺规作出 ,使得 ,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
25. 网格图中每个方格都是边长为 的正方形.若 ,,,,, 都是格点,试说明 .
26. 如图,在 的方格纸中, 是格点三角形(顶点在网格交点处).在图中画出与 相似的格点 和格点 ,使 与 的相似比是 , 与 的相似比是 .
答案
1. C
2. C
3. D
4. C
5. B
【解析】选项A,因为 ,,所以阴影三角形与原三角形相似,故A不合题意;
选项B,因为 且 ,所以阴影三角形与原三角形不相似,故B符合题意;
选项C,因为 ,,,所以阴影三角形与原三角形相似,故C不合题意;
选项D,因为 ,,所以阴影三角形与原三角形相似,故D不合题意.
故选B.
6. B
【解析】设每个小正方形的边长都为 ,由网格得,“帅”“相”“兵”所在位置的格点构成的三角形的三边的长分别为 ,,;“车”与“炮”之间的距离为 ,“炮”与②之间的距离为 ,“车”与②之间的距离为 ,
,
“马”应该落在②的位置.
7. A
8. C
【解析】在 和 中, 是公共角,,
,
,
又 的面积为 ,
的面积为 ,
的面积为 .
9. B
10. C
11. D
【解析】在矩形 中,
,
,,
,,
又 ,
,
,
又 ,
甲、乙、丙三个三角形相似,应选D.
12. C
13. D 【解析】设单位正方形的边长为 ,给出的三角形三边长分别为 ,,.
A.三角形三边分别是 ,,,与给出的三角形的各边不成比例,故A选项错误;
B.三角形三边 ,,,与给出的三角形的各边不成比例,故B选项错误;
C.三角形三边 ,,,与给出的三角形的各边不成比例,故C选项错误;
D.三角形三边 ,,,与给出的三角形的各边成正比例,故D选项正确.
14.
15. 答案不唯一,如 或 等
16.
17. 中的任意实数
【解析】,,,,
,,
若 ,则 ,即 ,解得 为任意实数,
又 ,
;
若 ,则 ,即 ,解得 (舍);
综上, 的值可能是 中的任意实数.
18.
【解析】,,,
,
,
,
,
设 ,则 ,
,
整理得 ,
点只有一个,
,
解得 .
19.
【解析】 两个相似三角形的最短边分别是 和 ,
两个三角形的相似比为 ,
设大三角形的周长为 ,则小三角形的周长为 ,
由题意得,,
解得,,
则 ,
故答案为:.
20. ,.
21. , ,
.
, 分别是 , 的平分线,
.
.
;;;.
22. 根据已知条件可得 ,.
①设经过 后 ,
,
,
解得 .
②设经过 后 ,
,
,
解得 .
故经过 或 后,以点 ,, 为顶点的三角形与 相似.
23. 与 相似.理由:
,,,,,,
,,,
,
.
24. ()
就是所求作的三角形.
()已知:如图,,,,.求证:.
证明:
因为 ,,
所以 ,,
所以 .
因为 ,
所以 ,.
在 和 中,
,且 ,
所以 ,
所以 .
25. ,,,,,,
,
.
26. 的边长分别为 ,,;
的边长分别为 ,,.
图略.
一、选择题(共13小题)
1. 如图,点 ,,,,,,,, 都是 方格纸中的格点,为使 ,则点 应是 ,,, 四点中的
A. B. C. D.
2. 与 相交于 ,,, 是 上的点,, 是 上的点,且 ,,则图中与 相似的三角形(不含 )共有
A. 个 B. 个 C. 个 D. 个
3. 要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为 ,,,另一个三角形框架的一边长为 ,它的另外两边长分别可以为
A. , B. ,
C. , D. , 或 , 或 ,
4. 如图,在大小为 的正方形网格中,是相似三角形的是
A. ①和② B. ②和③ C. ①和③ D. ②和④
5. 如图,在 中,,,,将 沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是
A. B.
C. D.
6. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”落在下列位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似的是
A. ①处 B. ②处 C. ③处 D. ④处
7. 如图,四个 的正方形网格(每个网格中的小正方形边长都是 ),每个网格中均有一个“格点三角形”(三角形的顶点在小正方形的顶点上),是相似三角形的为
A. ①③ B. ①② C. ②③ D. ②④
8. 如图,在 中,,, 为 边上的一点,且 .若 的面积为 ,则 的面积为
A. B. C. D.
9. 如图,在 中,,,.点 是边上 一动点,过点 作 交 于点 , 为线段 的中点,当 平分 时, 的长度为
A. B. C. D.
10. 一个三角形三边的长分别是 ,,,另一个与它相似的三角形的最长边是 ,则其他两边的和是
A. B. C. D.
11. 如图,点 、 分别在矩形 的边 , 上,,,则甲、乙、丙三个三角形中相似的是
A. 只有甲与乙 B. 只有乙与丙 C. 只有甲与丙 D. 甲与乙与丙
12. 如图,已知 .下列四个三角形,与 相似的是
A. B.
C. D.
13. 下列四个三角形,与如图中的三角形相似的是
A. B.
C. D.
二、填空题(共6小题)
14. 如图,如 ,则图中 .
15. 如图,, 分别是 的边 , 上的点,请你添加一个条件,使 与 相似,你添加的条件是 .
16. 如图,由边长为 的 个小正方形组成的网格中有一个与 相似且面积最大的 ,且它的三个顶点都落在小正方形的顶点上,则 的面积为 .
17. 如图, 中,,,点 , 分别在 , 上,其中 ,.当 与 相似时, 的值可能是 .
18. 如图,已知四边形 中,,,,,点 是边 上使 的点,当 时,这样的 点只有一个.
19. 两个相似三角形的最短边分别是 和 ,它们的周长之差是 ,那么小三角形的周长为 .
三、解答题(共7小题)
20. 已知:在 中, 比 大 ,,求 与 的度数.
21. 如图,在 中,,,, 分别是 , 的平分线,且相交于点 ,写出与 相似的三角形.
22. 如图所示,在 中,,,点 从点 开始沿 边以 的速度向点 移动,点 从点 开始沿 边以 的速度向点 移动,如果 , 分别从 , 两点同时出发,经几秒后,以点 ,, 为顶点的三角形与 相似
23. 如图,在边长为 的 的正方形网格上有两个三角形,它们的顶点都在格点上, 与 是否相似 请说明理由.
24. 求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的 及线段 ,(),以线段 为一边,在给出的图形上用尺规作出 ,使得 ,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
25. 网格图中每个方格都是边长为 的正方形.若 ,,,,, 都是格点,试说明 .
26. 如图,在 的方格纸中, 是格点三角形(顶点在网格交点处).在图中画出与 相似的格点 和格点 ,使 与 的相似比是 , 与 的相似比是 .
答案
1. C
2. C
3. D
4. C
5. B
【解析】选项A,因为 ,,所以阴影三角形与原三角形相似,故A不合题意;
选项B,因为 且 ,所以阴影三角形与原三角形不相似,故B符合题意;
选项C,因为 ,,,所以阴影三角形与原三角形相似,故C不合题意;
选项D,因为 ,,所以阴影三角形与原三角形相似,故D不合题意.
故选B.
6. B
【解析】设每个小正方形的边长都为 ,由网格得,“帅”“相”“兵”所在位置的格点构成的三角形的三边的长分别为 ,,;“车”与“炮”之间的距离为 ,“炮”与②之间的距离为 ,“车”与②之间的距离为 ,
,
“马”应该落在②的位置.
7. A
8. C
【解析】在 和 中, 是公共角,,
,
,
又 的面积为 ,
的面积为 ,
的面积为 .
9. B
10. C
11. D
【解析】在矩形 中,
,
,,
,,
又 ,
,
,
又 ,
甲、乙、丙三个三角形相似,应选D.
12. C
13. D 【解析】设单位正方形的边长为 ,给出的三角形三边长分别为 ,,.
A.三角形三边分别是 ,,,与给出的三角形的各边不成比例,故A选项错误;
B.三角形三边 ,,,与给出的三角形的各边不成比例,故B选项错误;
C.三角形三边 ,,,与给出的三角形的各边不成比例,故C选项错误;
D.三角形三边 ,,,与给出的三角形的各边成正比例,故D选项正确.
14.
15. 答案不唯一,如 或 等
16.
17. 中的任意实数
【解析】,,,,
,,
若 ,则 ,即 ,解得 为任意实数,
又 ,
;
若 ,则 ,即 ,解得 (舍);
综上, 的值可能是 中的任意实数.
18.
【解析】,,,
,
,
,
,
设 ,则 ,
,
整理得 ,
点只有一个,
,
解得 .
19.
【解析】 两个相似三角形的最短边分别是 和 ,
两个三角形的相似比为 ,
设大三角形的周长为 ,则小三角形的周长为 ,
由题意得,,
解得,,
则 ,
故答案为:.
20. ,.
21. , ,
.
, 分别是 , 的平分线,
.
.
;;;.
22. 根据已知条件可得 ,.
①设经过 后 ,
,
,
解得 .
②设经过 后 ,
,
,
解得 .
故经过 或 后,以点 ,, 为顶点的三角形与 相似.
23. 与 相似.理由:
,,,,,,
,,,
,
.
24. ()
就是所求作的三角形.
()已知:如图,,,,.求证:.
证明:
因为 ,,
所以 ,,
所以 .
因为 ,
所以 ,.
在 和 中,
,且 ,
所以 ,
所以 .
25. ,,,,,,
,
.
26. 的边长分别为 ,,;
的边长分别为 ,,.
图略.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
