北师大版九年级数学上册4.6利用相似三角形测高常考题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册4.6利用相似三角形测高常考题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 255.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 18:59:12 | ||
图片预览

文档简介
2022年北师大新版九年级(上)《4.6 利用相似三角形测高》常考题
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜手电筒的灯泡位于点处,手电筒的光从平面镜上点处反射后,恰好经过木板的边缘点,落在墙上的点处点到地面的高度,点到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为已知光在镜面反射中的入射角等于反射角,图中点、、、在同一水平面上,则灯泡到地面的高度为( )
A. B. C. D.
如图,某校数学兴趣小组利用标杆测量学校旗杆的高度,标杆高,测得,,则旗杆高度是( )
A.
B.
C.
D.
一个三角形木架三边长分别是,,,现要再做一个与其相似的三角形木架,而只有长为和的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边允许有余料,则不同的截法有( )
A. 一种 B. 两种 C. 三种 D. 四种
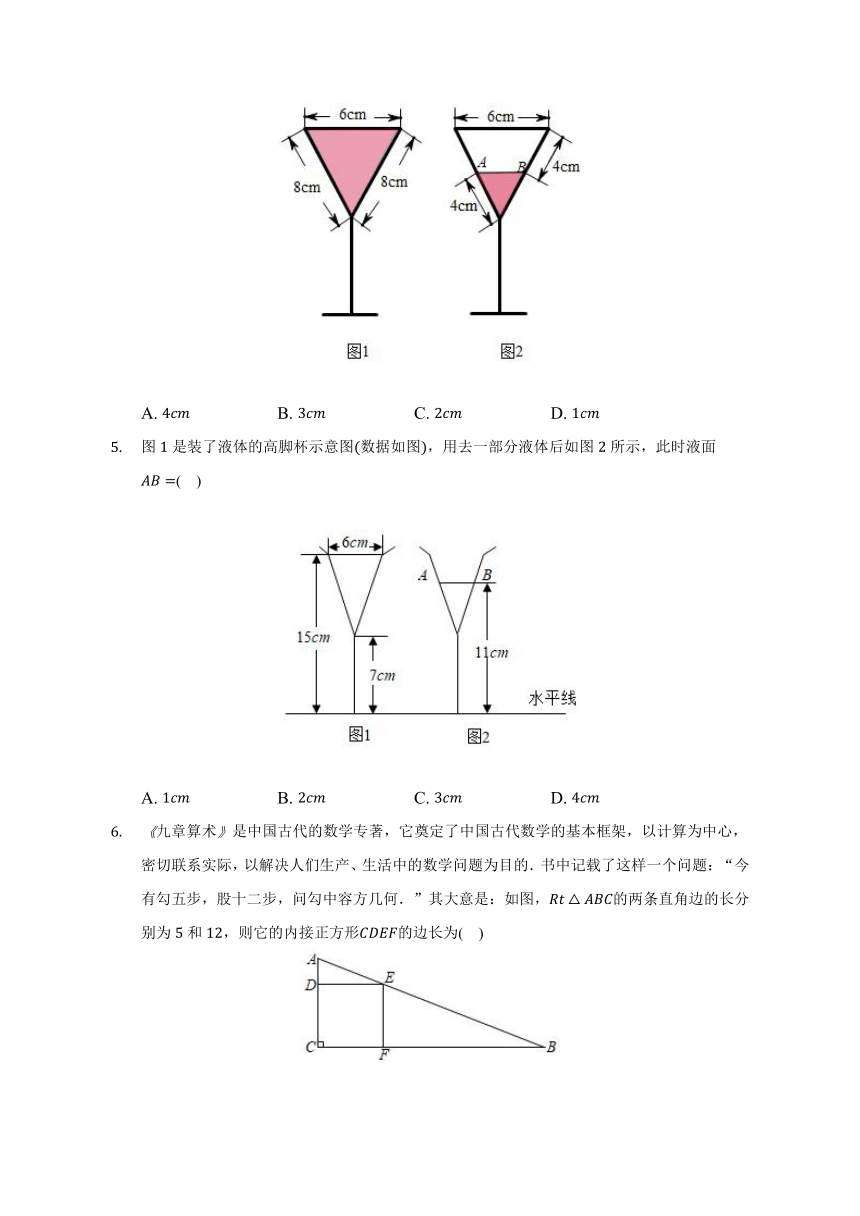
图是装满了液体的高脚杯数据如图,用去部分液体后,放在水平的桌面上如图所示,此时液面( )
A. B. C. D.
图是装了液体的高脚杯示意图数据如图,用去一部分液体后如图所示,此时液面( )
A. B. C. D.
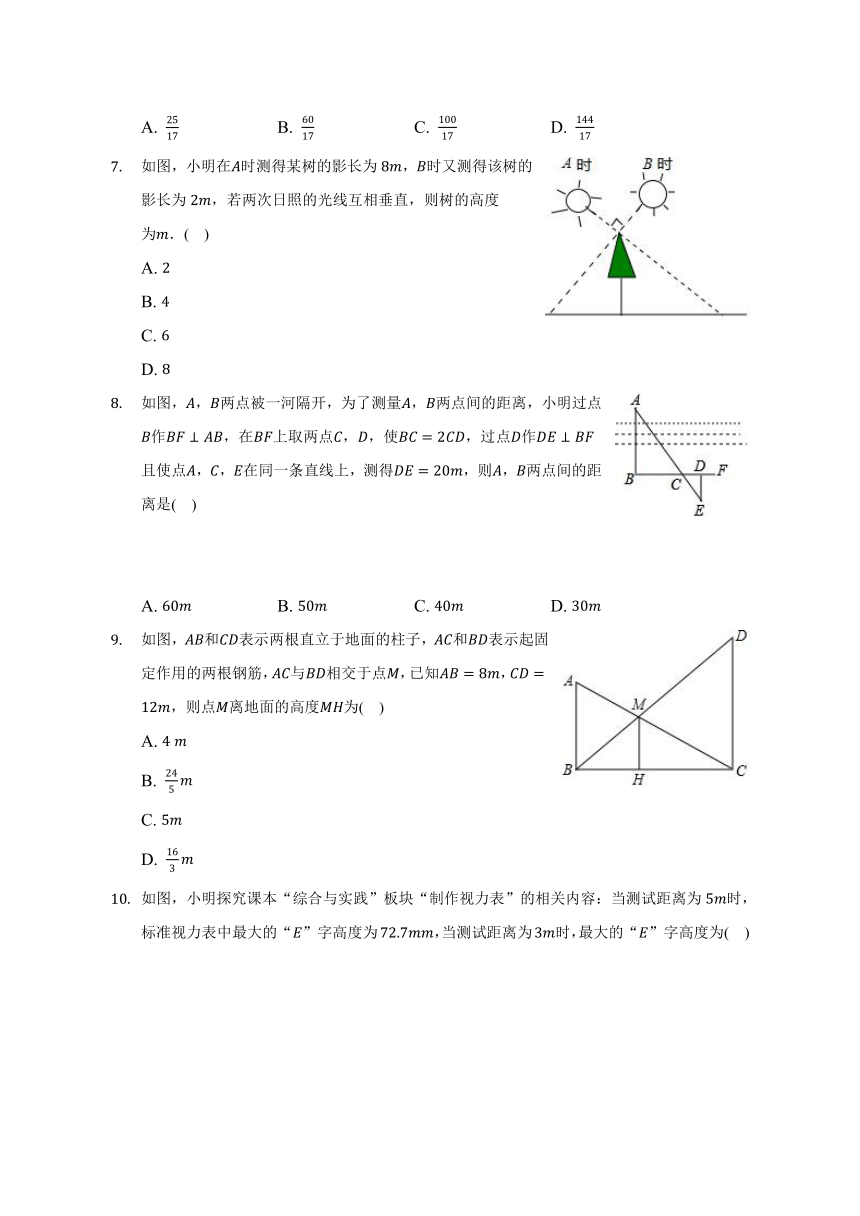
九章算术是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,的两条直角边的长分别为和,则它的内接正方形的边长为( )
A. B. C. D.
如图,小明在时测得某树的影长为,时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为.( )
A.
B.
C.
D.
如图,,两点被一河隔开,为了测量,两点间的距离,小明过点作,在上取两点,,使,过点作且使点,,在同一条直线上,测得,则,两点间的距离是( )
A. B. C. D.
如图,和表示两根直立于地面的柱子,和表示起固定作用的两根钢筋,与相交于点,已知,,则点离地面的高度为( )
A.
B.
C.
D.
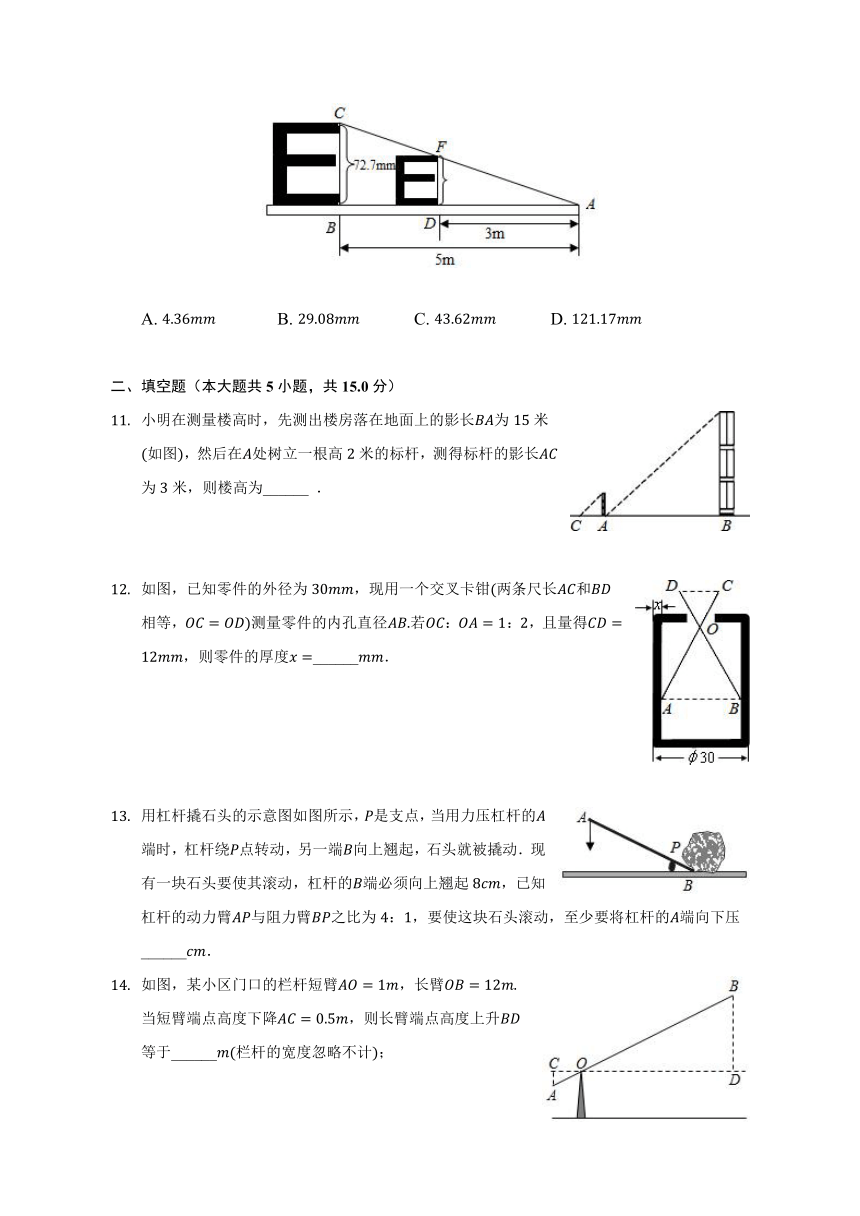
如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
小明在测量楼高时,先测出楼房落在地面上的影长为米如图,然后在处树立一根高米的标杆,测得标杆的影长为米,则楼高为______ .
如图,已知零件的外径为,现用一个交叉卡钳两条尺长和相等,测量零件的内孔直径若::,且量得,则零件的厚度______.
用杠杆撬石头的示意图如图所示,是支点,当用力压杠杆的端时,杠杆绕点转动,另一端向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的端必须向上翘起,已知杠杆的动力臂与阻力臂之比为:,要使这块石头滚动,至少要将杠杆的端向下压______.
如图,某小区门口的栏杆短臂,长臂当短臂端点高度下降,则长臂端点高度上升等于______栏杆的宽度忽略不计;
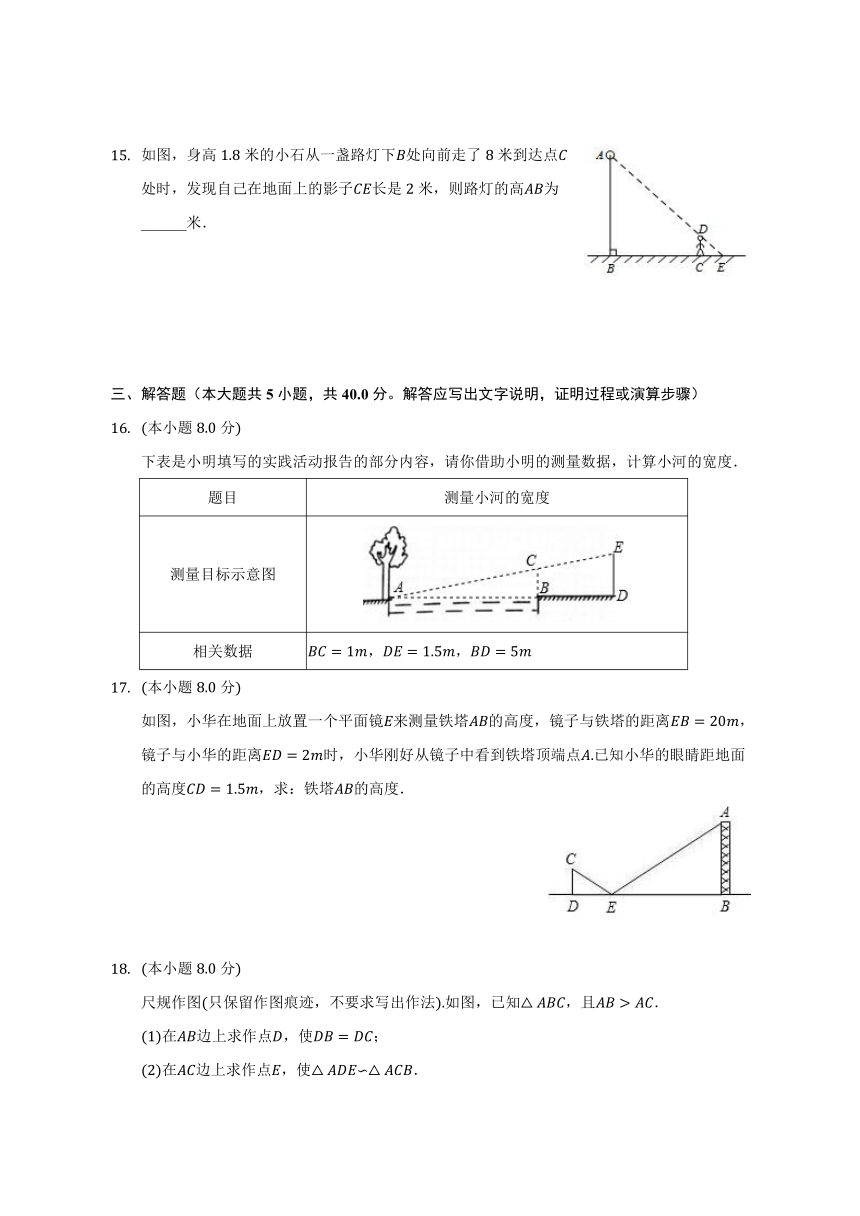
如图,身高米的小石从一盏路灯下处向前走了米到达点处时,发现自己在地面上的影子长是米,则路灯的高为______米.
三、解答题(本大题共5小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度
测量目标示意图
相关数据 ,,
本小题分
如图,小华在地面上放置一个平面镜来测量铁塔的高度,镜子与铁塔的距离,镜子与小华的距离时,小华刚好从镜子中看到铁塔顶端点已知小华的眼睛距地面的高度,求:铁塔的高度.
本小题分
尺规作图只保留作图痕迹,不要求写出作法如图,已知,且.
在边上求作点,使;
在边上求作点,使∽.
本小题分
定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图,在正方形网格中,格点线、将格点四边形分割成三个彼此相似的三角形.请你在图、图中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形.
本小题分
如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点处,手电筒的光从平面镜上点处反射后,恰好经过木板的边缘点,落在墙上的点处.点到地面的高度,点到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为已知光在镜面反射中的入射角等于反射角,图中点、、、在同一水平面上.
求的长.
求灯泡到地面的高度.
答案和解析
1.【答案】
【解析】解:由题意可得:,
则∽,
故,
即,
解得:,
则,
光在镜面反射中的入射角等于反射角,
,
又,
∽,
,
,
解得:,
故选:.
直接利用相似三角形的判定与性质得出的长,进而求出的长.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
2.【答案】
【解析】解:依题意得,
∽,
,即,
则.
故选:.
根据同一时刻同一地点物高与影长成正比列式求得的长即可.
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出直角三角形,难度不大.
3.【答案】
【解析】解:长的木条与三角形木架的最长边相等,则长的木条不能作为一边,
设从的木条上截下两段长分别为,,
若长的木条与的一边对应,则或,
解得:,不符合题意;
当长的木条与的一边对应,则或,
解得:,或,,,符合题意;
当长的木条与的一边对应,则或,
解得:,或,,,符合题意.
故有两种不同的截法:把的木条截下、两段或把的木条截下、两段.
故选:.
分类讨论:长的木条与三角形木架的最长边相等,则长的木条不能作为一边,设从的一根上截下的两段长分别为,,易得长的木条不能与的一边对应,所以当长的木条与的一边对应时有或;当长的木条与的一边对应时有或,然后分别利用比例的性质计算出两种情况下的和的值.
本题考查了相似三角形的应用:通常构建三角形相似,然后利用相似三角形的性质即相似三角形的对应边的比相等进行计算.
注意:把的木条截下、两段和把的木条截下、两段,属于同一种截法把的木条截下、两段和把的木条截下、两段,同理属于同一种截法.
4.【答案】
【解析】解:如图:,
∽,
,
,,,
,
,
故选:.
高脚杯前后的两个三角形相似,根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
5.【答案】
【解析】解:如图:过作,垂足为,过作,垂足为,
,
∽,即相似比为,
,
,,
,
,
故选:.
高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
6.【答案】
【解析】解:四边形是正方形,
,,
设,则,,
,
,,
∽,
,
,
,
正方形的边长为.
故选:.
根据正方形的性质得:,,则可证∽,列比例式可得结论.
此题考查了相似三角形的判定和性质、正方形的性质,设未知数构建方程是解题的关键.
7.【答案】
【解析】解:根据题意,作,树高为,且,,;
,,
,
∽,
,即,
解得.
故选:.
根据题意,画出示意图,易得:∽,进而可得,即,代入数据可得答案.
本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
8.【答案】
【解析】解:,,
,
∽,
,
即,
解得:,
故选:.
根据相似三角形的判定和性质解答即可.
此题考查相似三角形的应用,关键是根据相似三角形的判定得出∽解答.
9.【答案】
【解析】解:,
∽,
,相似三角形对应高的比等于相似比,
,
∽,
,
,
解得.
故选:.
根据已知易得∽,可得对应高与之比,易得,可得∽,利用对应边成比例可得比例式,把相关数值代入求解即可.
此题主要考查了相似三角形的应用;用到的知识点为:平行于三角形一边的直线与三角形另两边相交,截得的两三角形相似;相似三角形的对应边成比例;对应高的比等于相似比;解决本题的突破点是得到与的比.
10.【答案】
【解析】解:由题意得:,
,
,,,
,
,
故选:.
直接利用平行线分线段成比例定理列比例式,代入可得结论.
本题考查了相似三角形的应用,比较简单;根据生活常识,墙与地面垂直,则两张视力表平行,根据平行相似或平行线分线段成比例定理列比例式,可以计算出结果.
11.【答案】
【解析】解:
即,
楼高米.
故答案为:.
在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
12.【答案】
【解析】解:,,
,
,
又,
∽,
,
,
.
故答案为:.
利用两组对应边成比例,两三角形相似求出和相似,再根据相似三角形对应边成比例求出,然后求解即可.
本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,求出相似三角形是解题的关键.
13.【答案】
【解析】解:如图:、都与水平线垂直,即;
易知:∽;
,
杠杆的动力臂与阻力臂之比为:,
,即;
当时,;
故要使这块石头滚动,至少要将杠杆的端点向下压.
故答案为:.
首先根据题意构造出相似三角形,然后根据相似三角形的对应边成比例求得端点向下压的长度.
本题考查相似三角形的判定与性质的实际应用,正确的构造相似三角形是解题的关键.
14.【答案】
【解析】解:设长臂端点高度上升为米,
则,
解得:.
故答案为:.
栏杆长短臂在升降过程中,将形成两个相似三角形,利用对应变成比例解题.
此题考查了相似三角形在实际生活中的运用,得出比例关系式是解题关键.
15.【答案】
【解析】解:由题意知,米,米,米,,
则米,
,
∽
,即,
解得米,
即路灯的高为米;
故答案为:.
根据,得出∽,进而得出比例式求出即可.
此题主要考查了相似三角形的应用,得出∽是解决问题的关键.
16.【答案】解:由题意可得:∽,
则,
即,
解得:,
答:小河的宽度为.
【解析】直接利用相似三角形的判定与性质得出,进而得出答案.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
17.【答案】解:结合光的反射原理得:.
在和中,
,,
∽,
,
即,
解得.
答:铁塔的高度是.
【解析】根据反射定律可以推出,所以可得∽,再根据相似三角形的性质解答.
本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
18.【答案】解:如图,点即为所求.
如图,点即为所求.
【解析】作线段的垂直平分线交于点,连接即可.
作,射线交于点,点即为所求.
本题考查作图相似变换,线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.【答案】解:如图所示:
【解析】本题主要考查作图相似变换,根据题意,进行求解即可.
20.【答案】解:由题意可得:,
则∽,
故,
即,
解得:;
,
,
光在镜面反射中的入射角等于反射角,
,
又,
∽,
,
,
解得:,
答:灯泡到地面的高度为.
【解析】直接利用相似三角形的判定与性质得出的长;
根据相似三角形的性质列方程进而求出的长.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜手电筒的灯泡位于点处,手电筒的光从平面镜上点处反射后,恰好经过木板的边缘点,落在墙上的点处点到地面的高度,点到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为已知光在镜面反射中的入射角等于反射角,图中点、、、在同一水平面上,则灯泡到地面的高度为( )
A. B. C. D.
如图,某校数学兴趣小组利用标杆测量学校旗杆的高度,标杆高,测得,,则旗杆高度是( )
A.
B.
C.
D.
一个三角形木架三边长分别是,,,现要再做一个与其相似的三角形木架,而只有长为和的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边允许有余料,则不同的截法有( )
A. 一种 B. 两种 C. 三种 D. 四种
图是装满了液体的高脚杯数据如图,用去部分液体后,放在水平的桌面上如图所示,此时液面( )
A. B. C. D.
图是装了液体的高脚杯示意图数据如图,用去一部分液体后如图所示,此时液面( )
A. B. C. D.
九章算术是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,的两条直角边的长分别为和,则它的内接正方形的边长为( )
A. B. C. D.
如图,小明在时测得某树的影长为,时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为.( )
A.
B.
C.
D.
如图,,两点被一河隔开,为了测量,两点间的距离,小明过点作,在上取两点,,使,过点作且使点,,在同一条直线上,测得,则,两点间的距离是( )
A. B. C. D.
如图,和表示两根直立于地面的柱子,和表示起固定作用的两根钢筋,与相交于点,已知,,则点离地面的高度为( )
A.
B.
C.
D.
如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
小明在测量楼高时,先测出楼房落在地面上的影长为米如图,然后在处树立一根高米的标杆,测得标杆的影长为米,则楼高为______ .
如图,已知零件的外径为,现用一个交叉卡钳两条尺长和相等,测量零件的内孔直径若::,且量得,则零件的厚度______.
用杠杆撬石头的示意图如图所示,是支点,当用力压杠杆的端时,杠杆绕点转动,另一端向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的端必须向上翘起,已知杠杆的动力臂与阻力臂之比为:,要使这块石头滚动,至少要将杠杆的端向下压______.
如图,某小区门口的栏杆短臂,长臂当短臂端点高度下降,则长臂端点高度上升等于______栏杆的宽度忽略不计;
如图,身高米的小石从一盏路灯下处向前走了米到达点处时,发现自己在地面上的影子长是米,则路灯的高为______米.
三、解答题(本大题共5小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
本小题分
下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度
测量目标示意图
相关数据 ,,
本小题分
如图,小华在地面上放置一个平面镜来测量铁塔的高度,镜子与铁塔的距离,镜子与小华的距离时,小华刚好从镜子中看到铁塔顶端点已知小华的眼睛距地面的高度,求:铁塔的高度.
本小题分
尺规作图只保留作图痕迹,不要求写出作法如图,已知,且.
在边上求作点,使;
在边上求作点,使∽.
本小题分
定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图,在正方形网格中,格点线、将格点四边形分割成三个彼此相似的三角形.请你在图、图中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形.
本小题分
如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点处,手电筒的光从平面镜上点处反射后,恰好经过木板的边缘点,落在墙上的点处.点到地面的高度,点到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为已知光在镜面反射中的入射角等于反射角,图中点、、、在同一水平面上.
求的长.
求灯泡到地面的高度.
答案和解析
1.【答案】
【解析】解:由题意可得:,
则∽,
故,
即,
解得:,
则,
光在镜面反射中的入射角等于反射角,
,
又,
∽,
,
,
解得:,
故选:.
直接利用相似三角形的判定与性质得出的长,进而求出的长.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
2.【答案】
【解析】解:依题意得,
∽,
,即,
则.
故选:.
根据同一时刻同一地点物高与影长成正比列式求得的长即可.
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出直角三角形,难度不大.
3.【答案】
【解析】解:长的木条与三角形木架的最长边相等,则长的木条不能作为一边,
设从的木条上截下两段长分别为,,
若长的木条与的一边对应,则或,
解得:,不符合题意;
当长的木条与的一边对应,则或,
解得:,或,,,符合题意;
当长的木条与的一边对应,则或,
解得:,或,,,符合题意.
故有两种不同的截法:把的木条截下、两段或把的木条截下、两段.
故选:.
分类讨论:长的木条与三角形木架的最长边相等,则长的木条不能作为一边,设从的一根上截下的两段长分别为,,易得长的木条不能与的一边对应,所以当长的木条与的一边对应时有或;当长的木条与的一边对应时有或,然后分别利用比例的性质计算出两种情况下的和的值.
本题考查了相似三角形的应用:通常构建三角形相似,然后利用相似三角形的性质即相似三角形的对应边的比相等进行计算.
注意:把的木条截下、两段和把的木条截下、两段,属于同一种截法把的木条截下、两段和把的木条截下、两段,同理属于同一种截法.
4.【答案】
【解析】解:如图:,
∽,
,
,,,
,
,
故选:.
高脚杯前后的两个三角形相似,根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
5.【答案】
【解析】解:如图:过作,垂足为,过作,垂足为,
,
∽,即相似比为,
,
,,
,
,
故选:.
高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
6.【答案】
【解析】解:四边形是正方形,
,,
设,则,,
,
,,
∽,
,
,
,
正方形的边长为.
故选:.
根据正方形的性质得:,,则可证∽,列比例式可得结论.
此题考查了相似三角形的判定和性质、正方形的性质,设未知数构建方程是解题的关键.
7.【答案】
【解析】解:根据题意,作,树高为,且,,;
,,
,
∽,
,即,
解得.
故选:.
根据题意,画出示意图,易得:∽,进而可得,即,代入数据可得答案.
本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
8.【答案】
【解析】解:,,
,
∽,
,
即,
解得:,
故选:.
根据相似三角形的判定和性质解答即可.
此题考查相似三角形的应用,关键是根据相似三角形的判定得出∽解答.
9.【答案】
【解析】解:,
∽,
,相似三角形对应高的比等于相似比,
,
∽,
,
,
解得.
故选:.
根据已知易得∽,可得对应高与之比,易得,可得∽,利用对应边成比例可得比例式,把相关数值代入求解即可.
此题主要考查了相似三角形的应用;用到的知识点为:平行于三角形一边的直线与三角形另两边相交,截得的两三角形相似;相似三角形的对应边成比例;对应高的比等于相似比;解决本题的突破点是得到与的比.
10.【答案】
【解析】解:由题意得:,
,
,,,
,
,
故选:.
直接利用平行线分线段成比例定理列比例式,代入可得结论.
本题考查了相似三角形的应用,比较简单;根据生活常识,墙与地面垂直,则两张视力表平行,根据平行相似或平行线分线段成比例定理列比例式,可以计算出结果.
11.【答案】
【解析】解:
即,
楼高米.
故答案为:.
在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
12.【答案】
【解析】解:,,
,
,
又,
∽,
,
,
.
故答案为:.
利用两组对应边成比例,两三角形相似求出和相似,再根据相似三角形对应边成比例求出,然后求解即可.
本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,求出相似三角形是解题的关键.
13.【答案】
【解析】解:如图:、都与水平线垂直,即;
易知:∽;
,
杠杆的动力臂与阻力臂之比为:,
,即;
当时,;
故要使这块石头滚动,至少要将杠杆的端点向下压.
故答案为:.
首先根据题意构造出相似三角形,然后根据相似三角形的对应边成比例求得端点向下压的长度.
本题考查相似三角形的判定与性质的实际应用,正确的构造相似三角形是解题的关键.
14.【答案】
【解析】解:设长臂端点高度上升为米,
则,
解得:.
故答案为:.
栏杆长短臂在升降过程中,将形成两个相似三角形,利用对应变成比例解题.
此题考查了相似三角形在实际生活中的运用,得出比例关系式是解题关键.
15.【答案】
【解析】解:由题意知,米,米,米,,
则米,
,
∽
,即,
解得米,
即路灯的高为米;
故答案为:.
根据,得出∽,进而得出比例式求出即可.
此题主要考查了相似三角形的应用,得出∽是解决问题的关键.
16.【答案】解:由题意可得:∽,
则,
即,
解得:,
答:小河的宽度为.
【解析】直接利用相似三角形的判定与性质得出,进而得出答案.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
17.【答案】解:结合光的反射原理得:.
在和中,
,,
∽,
,
即,
解得.
答:铁塔的高度是.
【解析】根据反射定律可以推出,所以可得∽,再根据相似三角形的性质解答.
本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
18.【答案】解:如图,点即为所求.
如图,点即为所求.
【解析】作线段的垂直平分线交于点,连接即可.
作,射线交于点,点即为所求.
本题考查作图相似变换,线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.【答案】解:如图所示:
【解析】本题主要考查作图相似变换,根据题意,进行求解即可.
20.【答案】解:由题意可得:,
则∽,
故,
即,
解得:;
,
,
光在镜面反射中的入射角等于反射角,
,
又,
∽,
,
,
解得:,
答:灯泡到地面的高度为.
【解析】直接利用相似三角形的判定与性质得出的长;
根据相似三角形的性质列方程进而求出的长.
此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
