第一章 空间向量与立体几何 期末试题汇编(北京名校)-人教A版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 第一章 空间向量与立体几何 期末试题汇编(北京名校)-人教A版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 678.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 06:08:58 | ||
图片预览


文档简介
第一章 空间向量与立体几何 期末试题汇编(北京名校)
一.选择题
1.(2021秋 怀柔区期末)已知向量=(3,0,﹣4),则||=( )
A.5 B.6 C.7 D.8
2.(2021秋 石景山区期末)若=(2,﹣3,1),=(2,0,3),=(0,2,2),则 (+)的值为( )
A.3 B.4 C.7 D.15
3.(2021秋 顺义区期末)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.4 B. C.2 D.不确定
4.(2021秋 昌平区期末)已知平行六面体ABCD﹣A1B1C1D1中,设=,=,=,则=( )
A.﹣﹣﹣ B.﹣﹣ C.﹣+﹣ D.﹣+
5.(2022春 延庆区期末)下列命题错误的是( )
A.若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线
B.如果两条平行直线中的一条与一个平面平行,则另一条直线也与这个平面平行
C.如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行
D.一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角
6.(2021秋 西城区校级期末)已知平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),则( )
A.α∥β B.α⊥β
C.α,β相交但不垂直 D.α,β的位置关系不确定
7.(2021秋 顺义区期末)在空间直角坐标系中,若M(0,1,3),N(2,1,1),则=( )
A.(﹣2,0,2) B.(2,0,﹣2) C.(2,2,0) D.(2,2,﹣1)
8.(2021秋 大兴区期末)已知向量=(1,0,1),=(﹣2,2,1),=(3,4,z),若,,共面,则z等于( )
A.﹣9 B.﹣5 C.5 D.9
9.(2022春 大兴区期末)如图,在正方体ABCD﹣A1B1C1D1中,M是棱AB的中点.令直线D1M与AA1所成的角为θ1,直线D1M与平面A1B1C1D1所成的角为θ2,二面角D1﹣AM﹣C的平面角为θ3,则( )
A.θ1>θ2=θ3 B.θ1>θ3>θ2 C.θ1=θ2<θ3 D.θ1<θ3<θ2
10.(2021秋 西城区校级期末)已知长方体ABCD﹣A1B1C1D1中,AB=BC=4,CC1=2,则平面A1BC1与平面ABCD所成的锐二面角的余弦值为( )
A. B. C. D.
11.(2022春 丰台区校级期末)若一个正四棱锥的高和底面边长都为2,则它的侧面与底面所成角的余弦值为( )
A. B. C. D.
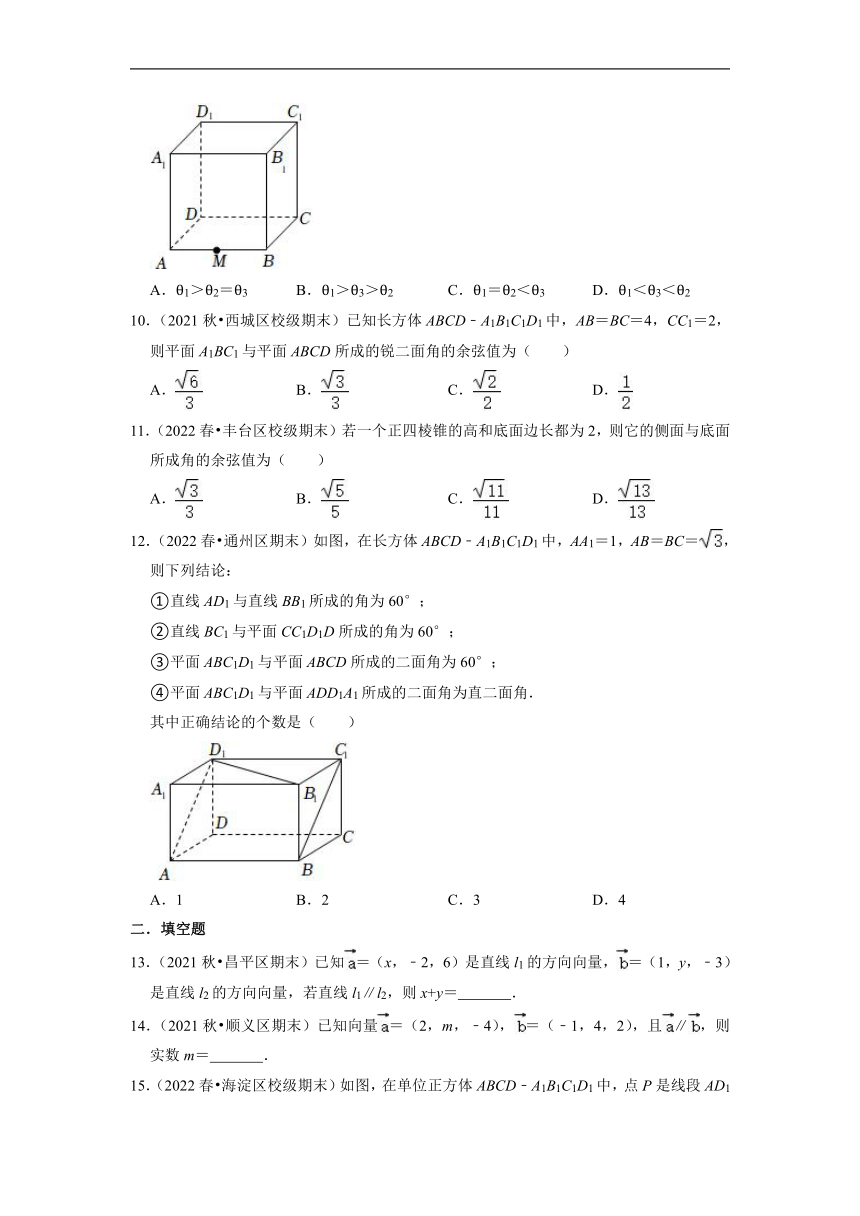
12.(2022春 通州区期末)如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=BC=,则下列结论:
①直线AD1与直线BB1所成的角为60°;
②直线BC1与平面CC1D1D所成的角为60°;
③平面ABC1D1与平面ABCD所成的二面角为60°;
④平面ABC1D1与平面ADD1A1所成的二面角为直二面角.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题
13.(2021秋 昌平区期末)已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= .
14.(2021秋 顺义区期末)已知向量=(2,m,﹣4),=(﹣1,4,2),且∥,则实数m= .
15.(2022春 海淀区校级期末)如图,在单位正方体ABCD﹣A1B1C1D1中,点P是线段AD1上的动点,给出以下四个命题:
①直线PC1与直线B1C所成角的大小为定值;
②二面角P﹣BC1﹣D的大小为定值;
③若Q是对角线AC1,上一点,则PQ+QC长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线A1C有可能平行.
其中真命题有 .
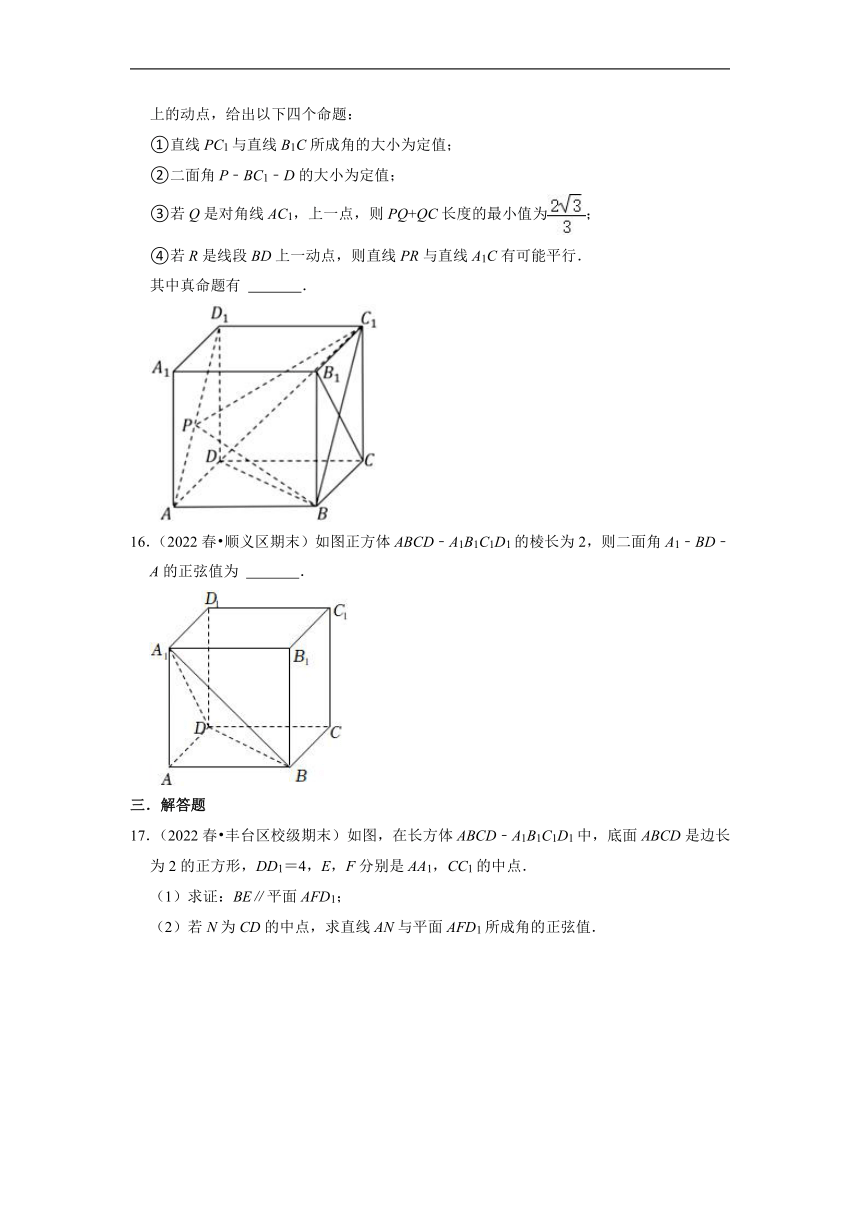
16.(2022春 顺义区期末)如图正方体ABCD﹣A1B1C1D1的棱长为2,则二面角A1﹣BD﹣A的正弦值为 .
三.解答题
17.(2022春 丰台区校级期末)如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,DD1=4,E,F分别是AA1,CC1的中点.
(1)求证:BE∥平面AFD1;
(2)若N为CD的中点,求直线AN与平面AFD1所成角的正弦值.
18.(2022春 大兴区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,点E在棱BB1上,且B1E=2BE,点F是棱DD1上的一个动点.
(1)点F在什么位置时,B1F∥平面AEC,并说明理由;
(2)若直线B1C与平面AFC所成角为60°,求二面角E﹣AC﹣F的余弦值.
19.(2022春 北京期末)在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=2,,CD=1,PA⊥平面ABCD,PA=2.
(Ⅰ)若E是PA的中点,求证:DE∥平面PBC;
(Ⅱ)求证:BD⊥平面PAC;
(Ⅲ)求BC与平面PAC所成角的正弦值.
20.(2022春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,AB=1.
(Ⅰ)求证:AB∥平面A1DCB1;
(Ⅱ)求证:BC1⊥平面A1DCB1;
(Ⅲ)求直线A1B和平面A1DCB1所成的角.
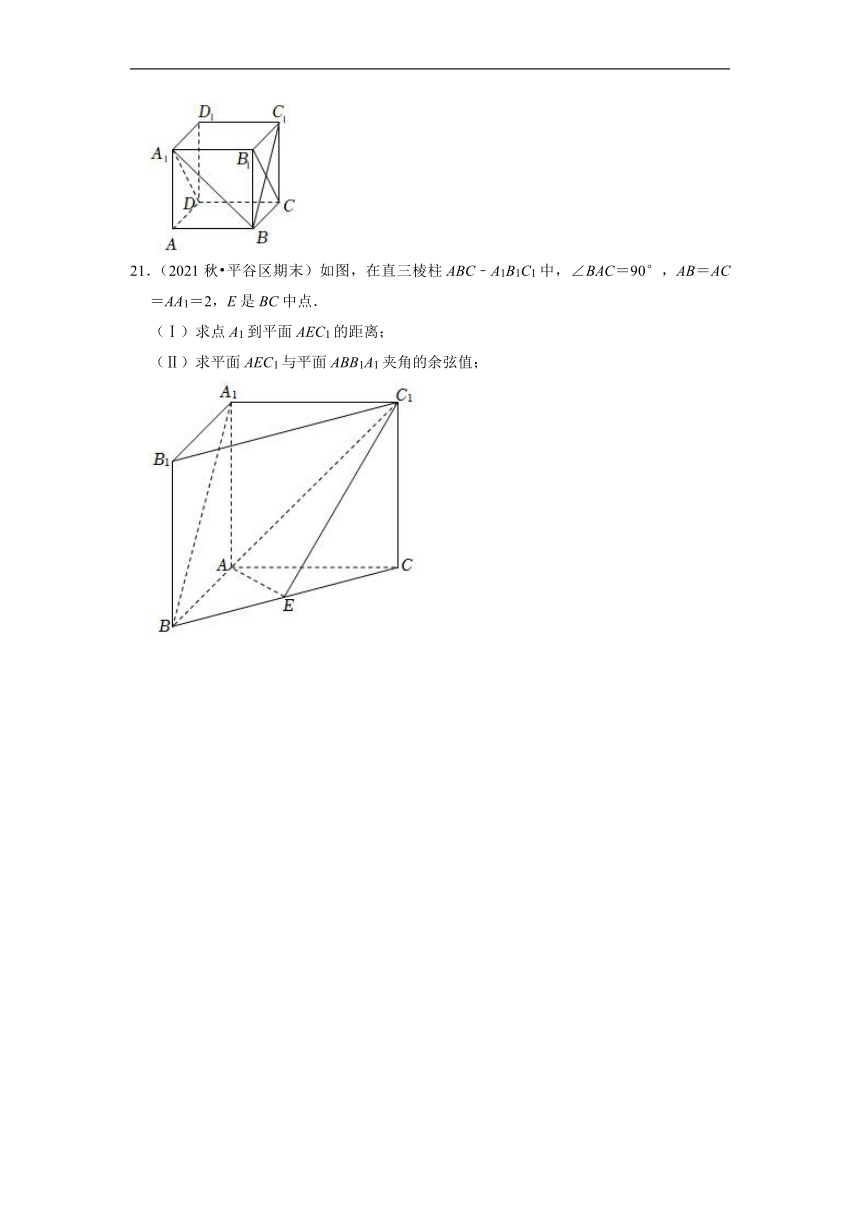
21.(2021秋 平谷区期末)如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
(Ⅰ)求点A1到平面AEC1的距离;
(Ⅱ)求平面AEC1与平面ABB1A1夹角的余弦值;
第一章 空间向量与立体几何 期末试题汇编(北京名校)
参考答案与试题解析
一.选择题(共12小题)
1.(2021秋 怀柔区期末)已知向量=(3,0,﹣4),则||=( )
A.5 B.6 C.7 D.8
【解答】解:因为向量=(3,0,﹣4),
则||==5.
故选:A.
2.(2021秋 石景山区期末)若=(2,﹣3,1),=(2,0,3),=(0,2,2),则 (+)的值为( )
A.3 B.4 C.7 D.15
【解答】解:依题意 ,所以.
故选:A.
3.(2021秋 顺义区期末)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.4 B. C.2 D.不确定
【解答】解:建立如图所示空间直角坐标系,
则A(2,0,0),P(0,2,x)(0≤x≤2),O(1,1,0),
∴=(﹣2,2,x)(0≤x≤2),=(﹣1,1,0),
∴.
故选:A.
4.(2021秋 昌平区期末)已知平行六面体ABCD﹣A1B1C1D1中,设=,=,=,则=( )
A.﹣﹣﹣ B.﹣﹣ C.﹣+﹣ D.﹣+
【解答】解:如图,
∵=,=,=,
∴===.
故选:B.
5.(2022春 延庆区期末)下列命题错误的是( )
A.若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线
B.如果两条平行直线中的一条与一个平面平行,则另一条直线也与这个平面平行
C.如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行
D.一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角
【解答】解:对于A,若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线,故正确,
对于B,如果两条平行直线中的一条与一个平面平行,则另一条直线可能与这个平面平行,也可能包含于这个平面,故错误,
对于C,如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行,故正确,
对于D,一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角,故正确,
故选:B.
6.(2021秋 西城区校级期末)已知平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),则( )
A.α∥β B.α⊥β
C.α,β相交但不垂直 D.α,β的位置关系不确定
【解答】解:平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),
对于A,∵,∴α,β不平行,故A错误;
对于B,=﹣6﹣3﹣20=﹣29≠0,∴α,β不垂直;
对于C,由A,B得α,β相交但不垂直,故C正确;
对于D,α,β相交但不垂直,故D错误.
故选:C.
7.(2021秋 顺义区期末)在空间直角坐标系中,若M(0,1,3),N(2,1,1),则=( )
A.(﹣2,0,2) B.(2,0,﹣2) C.(2,2,0) D.(2,2,﹣1)
【解答】解:∵在空间直角坐标系中,M(0,1,3),N(2,1,1),
∴=(2,0,﹣2).
故选:B.
8.(2021秋 大兴区期末)已知向量=(1,0,1),=(﹣2,2,1),=(3,4,z),若,,共面,则z等于( )
A.﹣9 B.﹣5 C.5 D.9
【解答】解:∵=(1,0,1),=(﹣2,2,1),=(3,4,z),,,共面,
∴存在实数x,y满足=x+y,
∴(1,0,1)=(﹣2x+3y,2x+4y,x+yz),
∴ ,
故选:D.
9.(2022春 大兴区期末)如图,在正方体ABCD﹣A1B1C1D1中,M是棱AB的中点.令直线D1M与AA1所成的角为θ1,直线D1M与平面A1B1C1D1所成的角为θ2,二面角D1﹣AM﹣C的平面角为θ3,则( )
A.θ1>θ2=θ3 B.θ1>θ3>θ2 C.θ1=θ2<θ3 D.θ1<θ3<θ2
【解答】解:取A1B1的中点N,连接如图,
易得AA1∥MN,故直线D1M与AA1所成的角θ1=∠D1MN,
又直线D1D⊥平面A1B1C1D1,
故直线D1M与平面A1B1C1D1所成的角为θ2=∠D1MD,
又AB⊥平面AA1D1D,
故二面角D1﹣AM﹣C的平面角为θ3=∠D1AD=45°,
因为,
故tanθ1>tanθ3>tanθ2,
又θ1,θ2,θ3均为锐角,故θ1>θ3>θ2.
故选:B.
10.(2021秋 西城区校级期末)已知长方体ABCD﹣A1B1C1D1中,AB=BC=4,CC1=2,则平面A1BC1与平面ABCD所成的锐二面角的余弦值为( )
A. B. C. D.
【解答】解:以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(4,0,2),B(4,4,0),C1(0,4,2),
∴=(0,4,﹣2),=(﹣4,4,0),
设平面A1BC1的一个法向量为=(x,y,z),
则,取z=2,则=(1,1,2),
平面ABCD的一个法向量为=(0,0,1),
设平面A1BC1与平面ABCD所成的锐二面角的平面角为θ,
则平面A1BC1与平面ABCD所成的锐二面角的余弦值为:
cosθ===.
故选:A.
11.(2022春 丰台区校级期末)若一个正四棱锥的高和底面边长都为2,则它的侧面与底面所成角的余弦值为( )
A. B. C. D.
【解答】解:如图,AC∩BD=O,H为AD中点,
在正四棱锥P﹣ABCD中,易知∠PHO为侧面与底面所成角,
又,则,
∴.
故选:B.
12.(2022春 通州区期末)如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=BC=,则下列结论:
①直线AD1与直线BB1所成的角为60°;
②直线BC1与平面CC1D1D所成的角为60°;
③平面ABC1D1与平面ABCD所成的二面角为60°;
④平面ABC1D1与平面ADD1A1所成的二面角为直二面角.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【解答】解:在长方体ABCD﹣A1B1C1D1中,有BB1∥AA1,
∴∠A1AD1为直线AD1与直线BB1所成的角,
又AA1=1,A1D1=,∴在Rt△A1AD1中,tan∠A1AD1==,
∴∠A1AD1=60°,故①正确;
由BC⊥平面CC1D1D,所以∠BC1C为直线BC1与平面CC1D1D所成的角,
在Rt△C1BC中,tan∠BC1C==,
∴∠BC1C=60°,故②正确;
∵AB⊥BC,AB⊥BC1,∴∠CBC1为二面角C1﹣BA﹣C的平面角,
由②知∠BC1C=60°,∴∠CBC1=30°,故③错误;
在长方体ABCD﹣A1B1C1D1中,有AB∥AA1,AB∥AD,
又AD∩AA1=A,∴AB⊥面ADD1A1,又AB 面ABC1D1,
∴面ABC1D1⊥面ADD1A1,
∴平面ABC1D1与平面ADD1A1所成的二面角为直二面角.故④正确.
故选:C.
二.填空题(共4小题)
13.(2021秋 昌平区期末)已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= ﹣1 .
【解答】解:=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,
若直线l1∥l2,则,
∴,则x=﹣2,y=1.
∴x+y=﹣2+1=﹣1.
故答案为:﹣1.
14.(2021秋 顺义区期末)已知向量=(2,m,﹣4),=(﹣1,4,2),且∥,则实数m= ﹣8 .
【解答】解:∵向量=(2,m,﹣4),=(﹣1,4,2),且∥,
∴,
解得实数m=﹣8.
故答案为:﹣8.
15.(2022春 海淀区校级期末)如图,在单位正方体ABCD﹣A1B1C1D1中,点P是线段AD1上的动点,给出以下四个命题:
①直线PC1与直线B1C所成角的大小为定值;
②二面角P﹣BC1﹣D的大小为定值;
③若Q是对角线AC1,上一点,则PQ+QC长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线A1C有可能平行.
其中真命题有 3个 .
【解答】解:对于①,由正方体的性质可知,B1C⊥平面ABC1D1,又PC1 平面ABC1D1,
故B1C⊥PC1,异面直线PC1与直线B1C的所成的角为定值,①正确;
对于②,平面PBC1即为平面ABC1D1,平面ABC1D1与平面BC1D所成的二面角为定值,
而这两个平面位置固定不变,故二面角P﹣BC1﹣D为定值,②正确;
对于③,将平面ACC1沿直线AC1翻折到平面ABC1D1内,平面图如下,
过C点做CP⊥AD1,CP∩AC1=Q,CP∩BC1=E,
此时,PQ+QC的值最小,
由题可知,,
,
则C1AC﹣1=,
故,又PE=AB=1,
故PQ+QC的最小值为,故③错误;
对于④,在正方体ABCD﹣A1B1C1D1中易证A1C⊥平面BDC1,
设AC∩BD=O,则∠A1OC1即为二面角A1﹣BD﹣C1的平面角,
又正方体棱长为1,故,则,
由余弦定理得,故,同理,
故在AA1上必然存在一点E,使得二面角E﹣BD﹣C1为,
即平面EBD⊥平面BDC1,平面EBD与平面ADD1A1的交线为ED,
则ED∩AD1=P,过P点作BD的垂线PR,此时PR⊥平面BDC1,
又A1C⊥平面BDC1,故PR∥A1C,故④正确.
故答案为:3个.
16.(2022春 顺义区期末)如图正方体ABCD﹣A1B1C1D1的棱长为2,则二面角A1﹣BD﹣A的正弦值为 .
【解答】解:如图,在正方体A1B1C1D1﹣ABCD中,设AC、BD交于O,连A1O,
∵BD⊥AC,BD⊥AA1,AC∩AA1=A,
∴BD⊥平面AA1O,
∴BD⊥A1O,
∴∠A1OA为二面角A1﹣BD﹣A的平面角.
在Rt△AlOA中,.
即截面A1BD与底面ABCD所成二面角A1﹣BD﹣A的正弦值等于.
故答案为:.
三.解答题(共5小题)
17.(2022春 丰台区校级期末)如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,DD1=4,E,F分别是AA1,CC1的中点.
(1)求证:BE∥平面AFD1;
(2)若N为CD的中点,求直线AN与平面AFD1所成角的正弦值.
【解答】(1)证明:如图所示,以点D为坐标原点,以DA,DC,DD1分别为x,y,z轴建立空间直角坐标系D﹣xyz,
由题得B(2,2,0),E(2,0,2),∴,
A(2,0,0),D1(0,0,4),F(0,2,2),∴,
设平面AFD1的法向量为,
所以,∴,
所以,
因为BE 平面AFD1,所以BE∥平面AFD1.
(2)解:由题得A(2,0,0),N(0,1,0),∴,
设直线AN与平面AFD,所成角为α,
所以.
所以直线AN与平面AED1所成角的正弦值为.
18.(2022春 大兴区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,点E在棱BB1上,且B1E=2BE,点F是棱DD1上的一个动点.
(1)点F在什么位置时,B1F∥平面AEC,并说明理由;
(2)若直线B1C与平面AFC所成角为60°,求二面角E﹣AC﹣F的余弦值.
【解答】解:(1)点F位于DD1的三等分点(靠近D点)时,B1F∥平面AEC,理由如下:
以A为坐标原点,分别以AB,AD,AA1所在直线为x轴,y轴,z轴建立空间直角坐标系,
设正方体棱长为3a,
则A(0,0,0),E(3a,0,a),C(3a,3a,0),B1(3a,0,3a),
=(3a,3a,0),=(3a,0,a),
设F(0,3a,t),
设平面ACE的法向量为=(x,y,z),
则,令x=1得:y=﹣1,z=﹣3,
所以,
因为,
令,
解得:t=a,
所以当点F位于DD1的三等分点(靠近D点)时,B1F∥平面AEC;
(2)设点F(0,3a,b),直线B1C与平面AFC所成角为60°,
设平面ACF的法向量为,=(0,3a,a),
则,令y1=1得:,
则,
所以,
解得:,
则=(﹣1,1,﹣2),
所以,
设二面角E﹣AC﹣F的大小为θ,显然θ为钝角,
则.
19.(2022春 北京期末)在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=2,,CD=1,PA⊥平面ABCD,PA=2.
(Ⅰ)若E是PA的中点,求证:DE∥平面PBC;
(Ⅱ)求证:BD⊥平面PAC;
(Ⅲ)求BC与平面PAC所成角的正弦值.
【解答】(Ⅰ)证明:取PB的中点M,连接ME,MC,
∵E是PA的中点,∴EM∥CAB,且ME=AB=1,
∵AB∥CD,CD=1,∴ME∥CD且ME=CD,
∴四边形MEDC是平行四边形,∴ED∥MC,
∵CM 平面PBC,DE 平面PBC,
∴DE∥平面PBC;
(Ⅱ)证明:∵PA⊥平面ABCD,BD 面ABCD,
∴BD⊥PA,
Rt△ABD中,tan∠ABD==,Rt△ACD中,tan∠DAC==,
∴tan∠ABD=tan∠DAC,结合∠ABD、∠DAC都是锐角,
得∠ABD=∠DAC=90°﹣∠ADB,
∴∠DAC+∠ADB=90°,得BD⊥AC,
∵PA∩AC=A,∴BD⊥平面PAC.
(Ⅲ)解:记BD∩AC于N,由(Ⅱ)知BD⊥平面PAC,
∴∠BCN为BC与平面PAC所成角,
由Rt△BAD,可得BD==,
∵BD×AN=AB×AD,解得AN==,
∴BN=,∵AC==,∴CN=,
∴BC==,
∴sin∠BCN==.
∴BC与平面PAC所成角的正弦值.
20.(2022春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,AB=1.
(Ⅰ)求证:AB∥平面A1DCB1;
(Ⅱ)求证:BC1⊥平面A1DCB1;
(Ⅲ)求直线A1B和平面A1DCB1所成的角.
【解答】(I)证明:∵AB∥A1B1,AB 平面A1B1CD,A1B1 平面A1B1CD,
∴AB∥平面A1B1CD.
(II)证明:在正方体ABCD﹣A1B1C1D1中,可得CD⊥平面BCC1B1,
又BC1 平面BCC1B1,∴CD⊥BC1,
由四边形BCC1B1是正方形,可得BC1⊥B1C,
又B1C∩CD=C,B1C,CD 平面A1DCB1,
∴BC1⊥平面A1DCB1;
(III)解:连接BC1交B1C于O,连接OA1,
∵四边形BCC1B1是正方形,∴OB⊥B1C,
∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1,
∴A1B1⊥OB,
又A1B1∩B1C=B1,
∴OB⊥平面A1B1CD,
∴∠OA1B为直线A1B和平面A1B1CD所成的角,
设正方体棱长为1,则A1B=,OB=,
∴sin∠OA1B==,
∴∠OA1B=30°,
∴直线A1B和平面A1B1CD所成的角为30°.
21.(2021秋 平谷区期末)如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
(Ⅰ)求点A1到平面AEC1的距离;
(Ⅱ)求平面AEC1与平面ABB1A1夹角的余弦值;
【解答】解:(I)以A为原点,AB为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
则A(0,0,0),A1(0,0,2),E(1,1,0),C1(0,2,2),
=(0,0,2),=(1,1,0),=(0,2,2),
设平面AEC1的法向量为=(x,y,z),
则,
取y=﹣1,得=(1,﹣1,1),
∴点A1到平面AEC1的距离d=||==.
∴点A1到平面AEC1的距离为.
(Ⅱ)解由(I)可得:B(2,0,0),B1(2,0,2),
所以=(﹣2,0,﹣2)
由(I)平面AEC1的一个法向量为=(1,﹣1,1),
因为AC⊥平面ABB1A1,取平面ABB1A1的法向量为=(0,2,0),
所以cos<,>==﹣,
平面AEC1与平面ABB1A1所成夹角的余弦值为.
一.选择题
1.(2021秋 怀柔区期末)已知向量=(3,0,﹣4),则||=( )
A.5 B.6 C.7 D.8
2.(2021秋 石景山区期末)若=(2,﹣3,1),=(2,0,3),=(0,2,2),则 (+)的值为( )
A.3 B.4 C.7 D.15
3.(2021秋 顺义区期末)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.4 B. C.2 D.不确定
4.(2021秋 昌平区期末)已知平行六面体ABCD﹣A1B1C1D1中,设=,=,=,则=( )
A.﹣﹣﹣ B.﹣﹣ C.﹣+﹣ D.﹣+
5.(2022春 延庆区期末)下列命题错误的是( )
A.若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线
B.如果两条平行直线中的一条与一个平面平行,则另一条直线也与这个平面平行
C.如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行
D.一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角
6.(2021秋 西城区校级期末)已知平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),则( )
A.α∥β B.α⊥β
C.α,β相交但不垂直 D.α,β的位置关系不确定
7.(2021秋 顺义区期末)在空间直角坐标系中,若M(0,1,3),N(2,1,1),则=( )
A.(﹣2,0,2) B.(2,0,﹣2) C.(2,2,0) D.(2,2,﹣1)
8.(2021秋 大兴区期末)已知向量=(1,0,1),=(﹣2,2,1),=(3,4,z),若,,共面,则z等于( )
A.﹣9 B.﹣5 C.5 D.9
9.(2022春 大兴区期末)如图,在正方体ABCD﹣A1B1C1D1中,M是棱AB的中点.令直线D1M与AA1所成的角为θ1,直线D1M与平面A1B1C1D1所成的角为θ2,二面角D1﹣AM﹣C的平面角为θ3,则( )
A.θ1>θ2=θ3 B.θ1>θ3>θ2 C.θ1=θ2<θ3 D.θ1<θ3<θ2
10.(2021秋 西城区校级期末)已知长方体ABCD﹣A1B1C1D1中,AB=BC=4,CC1=2,则平面A1BC1与平面ABCD所成的锐二面角的余弦值为( )
A. B. C. D.
11.(2022春 丰台区校级期末)若一个正四棱锥的高和底面边长都为2,则它的侧面与底面所成角的余弦值为( )
A. B. C. D.
12.(2022春 通州区期末)如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=BC=,则下列结论:
①直线AD1与直线BB1所成的角为60°;
②直线BC1与平面CC1D1D所成的角为60°;
③平面ABC1D1与平面ABCD所成的二面角为60°;
④平面ABC1D1与平面ADD1A1所成的二面角为直二面角.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题
13.(2021秋 昌平区期末)已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= .
14.(2021秋 顺义区期末)已知向量=(2,m,﹣4),=(﹣1,4,2),且∥,则实数m= .
15.(2022春 海淀区校级期末)如图,在单位正方体ABCD﹣A1B1C1D1中,点P是线段AD1上的动点,给出以下四个命题:
①直线PC1与直线B1C所成角的大小为定值;
②二面角P﹣BC1﹣D的大小为定值;
③若Q是对角线AC1,上一点,则PQ+QC长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线A1C有可能平行.
其中真命题有 .
16.(2022春 顺义区期末)如图正方体ABCD﹣A1B1C1D1的棱长为2,则二面角A1﹣BD﹣A的正弦值为 .
三.解答题
17.(2022春 丰台区校级期末)如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,DD1=4,E,F分别是AA1,CC1的中点.
(1)求证:BE∥平面AFD1;
(2)若N为CD的中点,求直线AN与平面AFD1所成角的正弦值.
18.(2022春 大兴区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,点E在棱BB1上,且B1E=2BE,点F是棱DD1上的一个动点.
(1)点F在什么位置时,B1F∥平面AEC,并说明理由;
(2)若直线B1C与平面AFC所成角为60°,求二面角E﹣AC﹣F的余弦值.
19.(2022春 北京期末)在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=2,,CD=1,PA⊥平面ABCD,PA=2.
(Ⅰ)若E是PA的中点,求证:DE∥平面PBC;
(Ⅱ)求证:BD⊥平面PAC;
(Ⅲ)求BC与平面PAC所成角的正弦值.
20.(2022春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,AB=1.
(Ⅰ)求证:AB∥平面A1DCB1;
(Ⅱ)求证:BC1⊥平面A1DCB1;
(Ⅲ)求直线A1B和平面A1DCB1所成的角.
21.(2021秋 平谷区期末)如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
(Ⅰ)求点A1到平面AEC1的距离;
(Ⅱ)求平面AEC1与平面ABB1A1夹角的余弦值;
第一章 空间向量与立体几何 期末试题汇编(北京名校)
参考答案与试题解析
一.选择题(共12小题)
1.(2021秋 怀柔区期末)已知向量=(3,0,﹣4),则||=( )
A.5 B.6 C.7 D.8
【解答】解:因为向量=(3,0,﹣4),
则||==5.
故选:A.
2.(2021秋 石景山区期末)若=(2,﹣3,1),=(2,0,3),=(0,2,2),则 (+)的值为( )
A.3 B.4 C.7 D.15
【解答】解:依题意 ,所以.
故选:A.
3.(2021秋 顺义区期末)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.4 B. C.2 D.不确定
【解答】解:建立如图所示空间直角坐标系,
则A(2,0,0),P(0,2,x)(0≤x≤2),O(1,1,0),
∴=(﹣2,2,x)(0≤x≤2),=(﹣1,1,0),
∴.
故选:A.
4.(2021秋 昌平区期末)已知平行六面体ABCD﹣A1B1C1D1中,设=,=,=,则=( )
A.﹣﹣﹣ B.﹣﹣ C.﹣+﹣ D.﹣+
【解答】解:如图,
∵=,=,=,
∴===.
故选:B.
5.(2022春 延庆区期末)下列命题错误的是( )
A.若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线
B.如果两条平行直线中的一条与一个平面平行,则另一条直线也与这个平面平行
C.如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行
D.一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角
【解答】解:对于A,若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任何一条直线,故正确,
对于B,如果两条平行直线中的一条与一个平面平行,则另一条直线可能与这个平面平行,也可能包含于这个平面,故错误,
对于C,如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行,故正确,
对于D,一个平面垂直于二面角的棱,它和二面角的两个面的交线形成的角就是二面角的一个平面角,故正确,
故选:B.
6.(2021秋 西城区校级期末)已知平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),则( )
A.α∥β B.α⊥β
C.α,β相交但不垂直 D.α,β的位置关系不确定
【解答】解:平面α,β的法向量分别为=(3,﹣1,4),=(﹣2,3,﹣5),
对于A,∵,∴α,β不平行,故A错误;
对于B,=﹣6﹣3﹣20=﹣29≠0,∴α,β不垂直;
对于C,由A,B得α,β相交但不垂直,故C正确;
对于D,α,β相交但不垂直,故D错误.
故选:C.
7.(2021秋 顺义区期末)在空间直角坐标系中,若M(0,1,3),N(2,1,1),则=( )
A.(﹣2,0,2) B.(2,0,﹣2) C.(2,2,0) D.(2,2,﹣1)
【解答】解:∵在空间直角坐标系中,M(0,1,3),N(2,1,1),
∴=(2,0,﹣2).
故选:B.
8.(2021秋 大兴区期末)已知向量=(1,0,1),=(﹣2,2,1),=(3,4,z),若,,共面,则z等于( )
A.﹣9 B.﹣5 C.5 D.9
【解答】解:∵=(1,0,1),=(﹣2,2,1),=(3,4,z),,,共面,
∴存在实数x,y满足=x+y,
∴(1,0,1)=(﹣2x+3y,2x+4y,x+yz),
∴ ,
故选:D.
9.(2022春 大兴区期末)如图,在正方体ABCD﹣A1B1C1D1中,M是棱AB的中点.令直线D1M与AA1所成的角为θ1,直线D1M与平面A1B1C1D1所成的角为θ2,二面角D1﹣AM﹣C的平面角为θ3,则( )
A.θ1>θ2=θ3 B.θ1>θ3>θ2 C.θ1=θ2<θ3 D.θ1<θ3<θ2
【解答】解:取A1B1的中点N,连接如图,
易得AA1∥MN,故直线D1M与AA1所成的角θ1=∠D1MN,
又直线D1D⊥平面A1B1C1D1,
故直线D1M与平面A1B1C1D1所成的角为θ2=∠D1MD,
又AB⊥平面AA1D1D,
故二面角D1﹣AM﹣C的平面角为θ3=∠D1AD=45°,
因为,
故tanθ1>tanθ3>tanθ2,
又θ1,θ2,θ3均为锐角,故θ1>θ3>θ2.
故选:B.
10.(2021秋 西城区校级期末)已知长方体ABCD﹣A1B1C1D1中,AB=BC=4,CC1=2,则平面A1BC1与平面ABCD所成的锐二面角的余弦值为( )
A. B. C. D.
【解答】解:以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(4,0,2),B(4,4,0),C1(0,4,2),
∴=(0,4,﹣2),=(﹣4,4,0),
设平面A1BC1的一个法向量为=(x,y,z),
则,取z=2,则=(1,1,2),
平面ABCD的一个法向量为=(0,0,1),
设平面A1BC1与平面ABCD所成的锐二面角的平面角为θ,
则平面A1BC1与平面ABCD所成的锐二面角的余弦值为:
cosθ===.
故选:A.
11.(2022春 丰台区校级期末)若一个正四棱锥的高和底面边长都为2,则它的侧面与底面所成角的余弦值为( )
A. B. C. D.
【解答】解:如图,AC∩BD=O,H为AD中点,
在正四棱锥P﹣ABCD中,易知∠PHO为侧面与底面所成角,
又,则,
∴.
故选:B.
12.(2022春 通州区期末)如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=BC=,则下列结论:
①直线AD1与直线BB1所成的角为60°;
②直线BC1与平面CC1D1D所成的角为60°;
③平面ABC1D1与平面ABCD所成的二面角为60°;
④平面ABC1D1与平面ADD1A1所成的二面角为直二面角.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【解答】解:在长方体ABCD﹣A1B1C1D1中,有BB1∥AA1,
∴∠A1AD1为直线AD1与直线BB1所成的角,
又AA1=1,A1D1=,∴在Rt△A1AD1中,tan∠A1AD1==,
∴∠A1AD1=60°,故①正确;
由BC⊥平面CC1D1D,所以∠BC1C为直线BC1与平面CC1D1D所成的角,
在Rt△C1BC中,tan∠BC1C==,
∴∠BC1C=60°,故②正确;
∵AB⊥BC,AB⊥BC1,∴∠CBC1为二面角C1﹣BA﹣C的平面角,
由②知∠BC1C=60°,∴∠CBC1=30°,故③错误;
在长方体ABCD﹣A1B1C1D1中,有AB∥AA1,AB∥AD,
又AD∩AA1=A,∴AB⊥面ADD1A1,又AB 面ABC1D1,
∴面ABC1D1⊥面ADD1A1,
∴平面ABC1D1与平面ADD1A1所成的二面角为直二面角.故④正确.
故选:C.
二.填空题(共4小题)
13.(2021秋 昌平区期末)已知=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,若直线l1∥l2,则x+y= ﹣1 .
【解答】解:=(x,﹣2,6)是直线l1的方向向量,=(1,y,﹣3)是直线l2的方向向量,
若直线l1∥l2,则,
∴,则x=﹣2,y=1.
∴x+y=﹣2+1=﹣1.
故答案为:﹣1.
14.(2021秋 顺义区期末)已知向量=(2,m,﹣4),=(﹣1,4,2),且∥,则实数m= ﹣8 .
【解答】解:∵向量=(2,m,﹣4),=(﹣1,4,2),且∥,
∴,
解得实数m=﹣8.
故答案为:﹣8.
15.(2022春 海淀区校级期末)如图,在单位正方体ABCD﹣A1B1C1D1中,点P是线段AD1上的动点,给出以下四个命题:
①直线PC1与直线B1C所成角的大小为定值;
②二面角P﹣BC1﹣D的大小为定值;
③若Q是对角线AC1,上一点,则PQ+QC长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线A1C有可能平行.
其中真命题有 3个 .
【解答】解:对于①,由正方体的性质可知,B1C⊥平面ABC1D1,又PC1 平面ABC1D1,
故B1C⊥PC1,异面直线PC1与直线B1C的所成的角为定值,①正确;
对于②,平面PBC1即为平面ABC1D1,平面ABC1D1与平面BC1D所成的二面角为定值,
而这两个平面位置固定不变,故二面角P﹣BC1﹣D为定值,②正确;
对于③,将平面ACC1沿直线AC1翻折到平面ABC1D1内,平面图如下,
过C点做CP⊥AD1,CP∩AC1=Q,CP∩BC1=E,
此时,PQ+QC的值最小,
由题可知,,
,
则C1AC﹣1=,
故,又PE=AB=1,
故PQ+QC的最小值为,故③错误;
对于④,在正方体ABCD﹣A1B1C1D1中易证A1C⊥平面BDC1,
设AC∩BD=O,则∠A1OC1即为二面角A1﹣BD﹣C1的平面角,
又正方体棱长为1,故,则,
由余弦定理得,故,同理,
故在AA1上必然存在一点E,使得二面角E﹣BD﹣C1为,
即平面EBD⊥平面BDC1,平面EBD与平面ADD1A1的交线为ED,
则ED∩AD1=P,过P点作BD的垂线PR,此时PR⊥平面BDC1,
又A1C⊥平面BDC1,故PR∥A1C,故④正确.
故答案为:3个.
16.(2022春 顺义区期末)如图正方体ABCD﹣A1B1C1D1的棱长为2,则二面角A1﹣BD﹣A的正弦值为 .
【解答】解:如图,在正方体A1B1C1D1﹣ABCD中,设AC、BD交于O,连A1O,
∵BD⊥AC,BD⊥AA1,AC∩AA1=A,
∴BD⊥平面AA1O,
∴BD⊥A1O,
∴∠A1OA为二面角A1﹣BD﹣A的平面角.
在Rt△AlOA中,.
即截面A1BD与底面ABCD所成二面角A1﹣BD﹣A的正弦值等于.
故答案为:.
三.解答题(共5小题)
17.(2022春 丰台区校级期末)如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,DD1=4,E,F分别是AA1,CC1的中点.
(1)求证:BE∥平面AFD1;
(2)若N为CD的中点,求直线AN与平面AFD1所成角的正弦值.
【解答】(1)证明:如图所示,以点D为坐标原点,以DA,DC,DD1分别为x,y,z轴建立空间直角坐标系D﹣xyz,
由题得B(2,2,0),E(2,0,2),∴,
A(2,0,0),D1(0,0,4),F(0,2,2),∴,
设平面AFD1的法向量为,
所以,∴,
所以,
因为BE 平面AFD1,所以BE∥平面AFD1.
(2)解:由题得A(2,0,0),N(0,1,0),∴,
设直线AN与平面AFD,所成角为α,
所以.
所以直线AN与平面AED1所成角的正弦值为.
18.(2022春 大兴区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,点E在棱BB1上,且B1E=2BE,点F是棱DD1上的一个动点.
(1)点F在什么位置时,B1F∥平面AEC,并说明理由;
(2)若直线B1C与平面AFC所成角为60°,求二面角E﹣AC﹣F的余弦值.
【解答】解:(1)点F位于DD1的三等分点(靠近D点)时,B1F∥平面AEC,理由如下:
以A为坐标原点,分别以AB,AD,AA1所在直线为x轴,y轴,z轴建立空间直角坐标系,
设正方体棱长为3a,
则A(0,0,0),E(3a,0,a),C(3a,3a,0),B1(3a,0,3a),
=(3a,3a,0),=(3a,0,a),
设F(0,3a,t),
设平面ACE的法向量为=(x,y,z),
则,令x=1得:y=﹣1,z=﹣3,
所以,
因为,
令,
解得:t=a,
所以当点F位于DD1的三等分点(靠近D点)时,B1F∥平面AEC;
(2)设点F(0,3a,b),直线B1C与平面AFC所成角为60°,
设平面ACF的法向量为,=(0,3a,a),
则,令y1=1得:,
则,
所以,
解得:,
则=(﹣1,1,﹣2),
所以,
设二面角E﹣AC﹣F的大小为θ,显然θ为钝角,
则.
19.(2022春 北京期末)在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=2,,CD=1,PA⊥平面ABCD,PA=2.
(Ⅰ)若E是PA的中点,求证:DE∥平面PBC;
(Ⅱ)求证:BD⊥平面PAC;
(Ⅲ)求BC与平面PAC所成角的正弦值.
【解答】(Ⅰ)证明:取PB的中点M,连接ME,MC,
∵E是PA的中点,∴EM∥CAB,且ME=AB=1,
∵AB∥CD,CD=1,∴ME∥CD且ME=CD,
∴四边形MEDC是平行四边形,∴ED∥MC,
∵CM 平面PBC,DE 平面PBC,
∴DE∥平面PBC;
(Ⅱ)证明:∵PA⊥平面ABCD,BD 面ABCD,
∴BD⊥PA,
Rt△ABD中,tan∠ABD==,Rt△ACD中,tan∠DAC==,
∴tan∠ABD=tan∠DAC,结合∠ABD、∠DAC都是锐角,
得∠ABD=∠DAC=90°﹣∠ADB,
∴∠DAC+∠ADB=90°,得BD⊥AC,
∵PA∩AC=A,∴BD⊥平面PAC.
(Ⅲ)解:记BD∩AC于N,由(Ⅱ)知BD⊥平面PAC,
∴∠BCN为BC与平面PAC所成角,
由Rt△BAD,可得BD==,
∵BD×AN=AB×AD,解得AN==,
∴BN=,∵AC==,∴CN=,
∴BC==,
∴sin∠BCN==.
∴BC与平面PAC所成角的正弦值.
20.(2022春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,AB=1.
(Ⅰ)求证:AB∥平面A1DCB1;
(Ⅱ)求证:BC1⊥平面A1DCB1;
(Ⅲ)求直线A1B和平面A1DCB1所成的角.
【解答】(I)证明:∵AB∥A1B1,AB 平面A1B1CD,A1B1 平面A1B1CD,
∴AB∥平面A1B1CD.
(II)证明:在正方体ABCD﹣A1B1C1D1中,可得CD⊥平面BCC1B1,
又BC1 平面BCC1B1,∴CD⊥BC1,
由四边形BCC1B1是正方形,可得BC1⊥B1C,
又B1C∩CD=C,B1C,CD 平面A1DCB1,
∴BC1⊥平面A1DCB1;
(III)解:连接BC1交B1C于O,连接OA1,
∵四边形BCC1B1是正方形,∴OB⊥B1C,
∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1,
∴A1B1⊥OB,
又A1B1∩B1C=B1,
∴OB⊥平面A1B1CD,
∴∠OA1B为直线A1B和平面A1B1CD所成的角,
设正方体棱长为1,则A1B=,OB=,
∴sin∠OA1B==,
∴∠OA1B=30°,
∴直线A1B和平面A1B1CD所成的角为30°.
21.(2021秋 平谷区期末)如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
(Ⅰ)求点A1到平面AEC1的距离;
(Ⅱ)求平面AEC1与平面ABB1A1夹角的余弦值;
【解答】解:(I)以A为原点,AB为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
则A(0,0,0),A1(0,0,2),E(1,1,0),C1(0,2,2),
=(0,0,2),=(1,1,0),=(0,2,2),
设平面AEC1的法向量为=(x,y,z),
则,
取y=﹣1,得=(1,﹣1,1),
∴点A1到平面AEC1的距离d=||==.
∴点A1到平面AEC1的距离为.
(Ⅱ)解由(I)可得:B(2,0,0),B1(2,0,2),
所以=(﹣2,0,﹣2)
由(I)平面AEC1的一个法向量为=(1,﹣1,1),
因为AC⊥平面ABB1A1,取平面ABB1A1的法向量为=(0,2,0),
所以cos<,>==﹣,
平面AEC1与平面ABB1A1所成夹角的余弦值为.
