第一章 空间向量与立体几何 单元测试-人教A版(2019)选择性必修第一册(含答案)
文档属性
| 名称 | 第一章 空间向量与立体几何 单元测试-人教A版(2019)选择性必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 06:09:57 | ||
图片预览


文档简介
高中数学人教A版(2019)选择性必修一空间向量与立体几何单元测试
一、单选题
1.已知点 , ,则线段 的中点 的坐标为( )
A. B. C. D.
2.如果向量 , , 共面,则实数 的值是( )
A.-1 B.1 C.-5 D.5
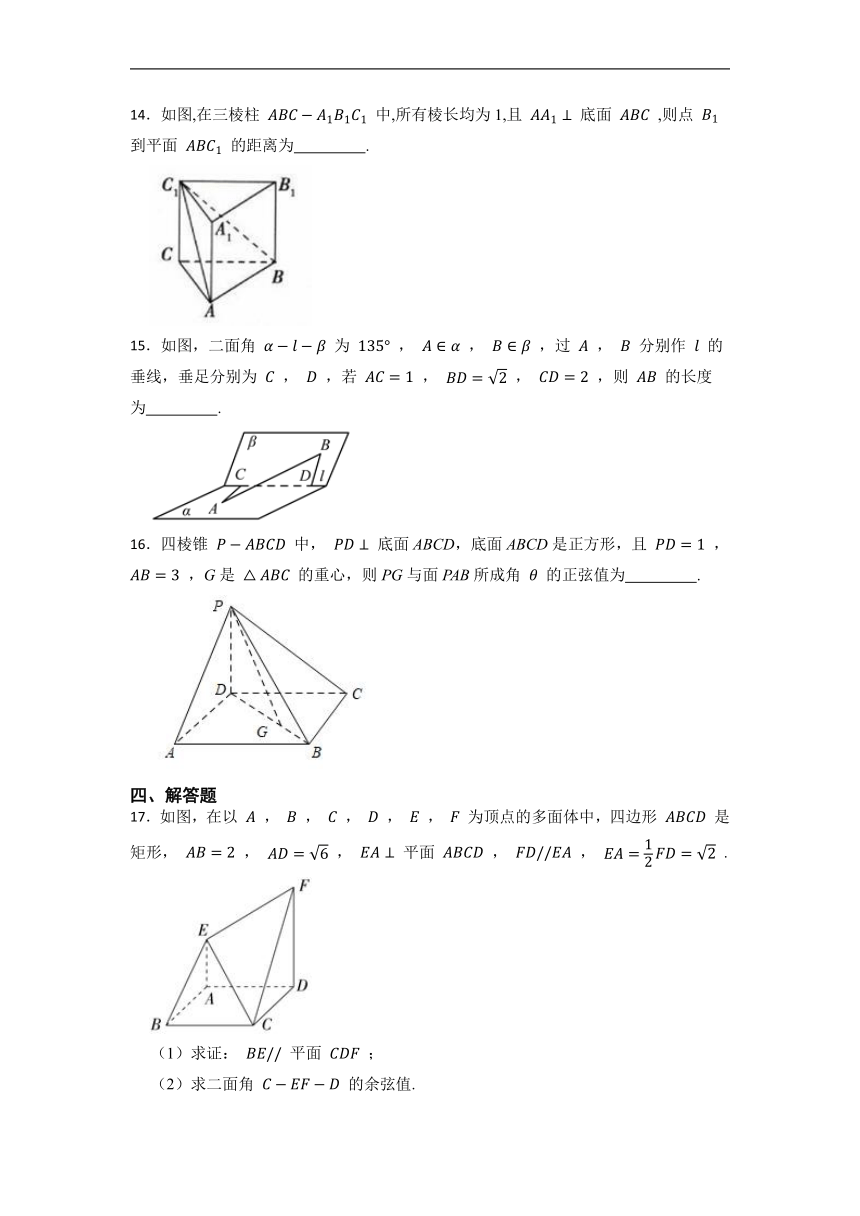
3.已知O,A,B,C为空间不共面的四点,且向量 = ,向量 ,则不能与 构成空间的一个基底的是( )
A. B.
C. D. 或
4.已知向量 和 分别是直线 和 的方向向量,则直线 与 所成的角为( )
A. B. C. D.
5.若向量 , 且 与 的夹角余弦为 ,则λ等于( )
A. B. C. 或 D.2
6.如图,在空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,B1E1= A1B1,则 等于( )
A. B. C. D.
7.设 ,向量 , , ,且 , ,则 ( )
A. B.3 C. D.4
8.已知正四面体 的各棱长为1,点 是 的中点,则 的值为( )
A. B. C. D.
二、多选题
9.已知M(-1,1,3),N(-2,-1,4),若M,N,O三点共线,则O点坐标可能为( )
A.(3,5,-2) B.(-4,-5,6)
C.( , , ) D.(0,3,2)
10.空间直角坐标系中,下列说法正确的是( )
A.点 关于坐标平面 的对称点的坐标为
B.点 在平面 面上
C. 表示一个与坐标平面 平行的平面
D. 表示一条直线
11.在长方体 中, , ,以D为原点, , , 的方向分别为x轴,y轴,z轴正方向建立空间直角坐标系,则下列说法正确的是( )
A. 的坐标为(2,2,3)
B. =(-2,0,3)
C.平面 的一个法向量为(-3,3,-2)
D.二面角 的余弦值为
12.设动点 在正方体 的对角线 上,记 当 为钝角时,则实数可能的取值是( )
A. B. C. D.1
三、填空题
13.如图所示,在正方体 中,点 为线段 的中点,点 在线段 上移动,异面直线 与 所成角最小时,其余弦值为 .
14.如图,在三棱柱 中,所有棱长均为1,且 底面 ,则点 到平面 的距离为 .
15.如图,二面角 为 , , ,过 , 分别作 的垂线,垂足分别为 , ,若 , , ,则 的长度为 .
16.四棱锥 中, 底面ABCD,底面ABCD是正方形,且 , ,G是 的重心,则PG与面PAB所成角 的正弦值为 .
四、解答题
17.如图,在以 , , , , , 为顶点的多面体中,四边形 是矩形, , , 平面 , , .
(1)求证: 平面 ;
(2)求二面角 的余弦值.
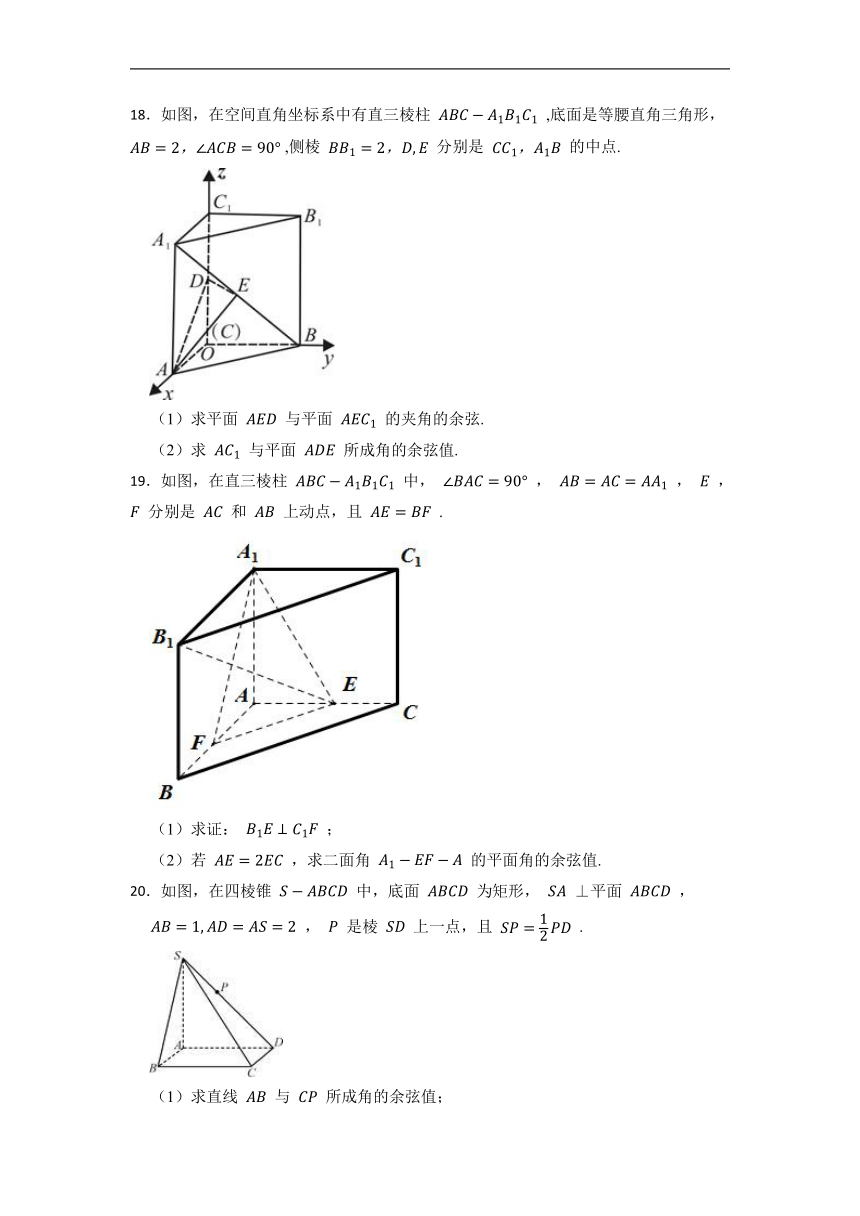
18.如图,在空间直角坐标系中有直三棱柱 ,底面是等腰直角三角形, ,侧棱 分别是 的中点.
(1)求平面 与平面 的夹角的余弦.
(2)求 与平面 所成角的余弦值.
19.如图,在直三棱柱 中, , , , 分别是 和 上动点,且 .
(1)求证: ;
(2)若 ,求二面角 的平面角的余弦值.
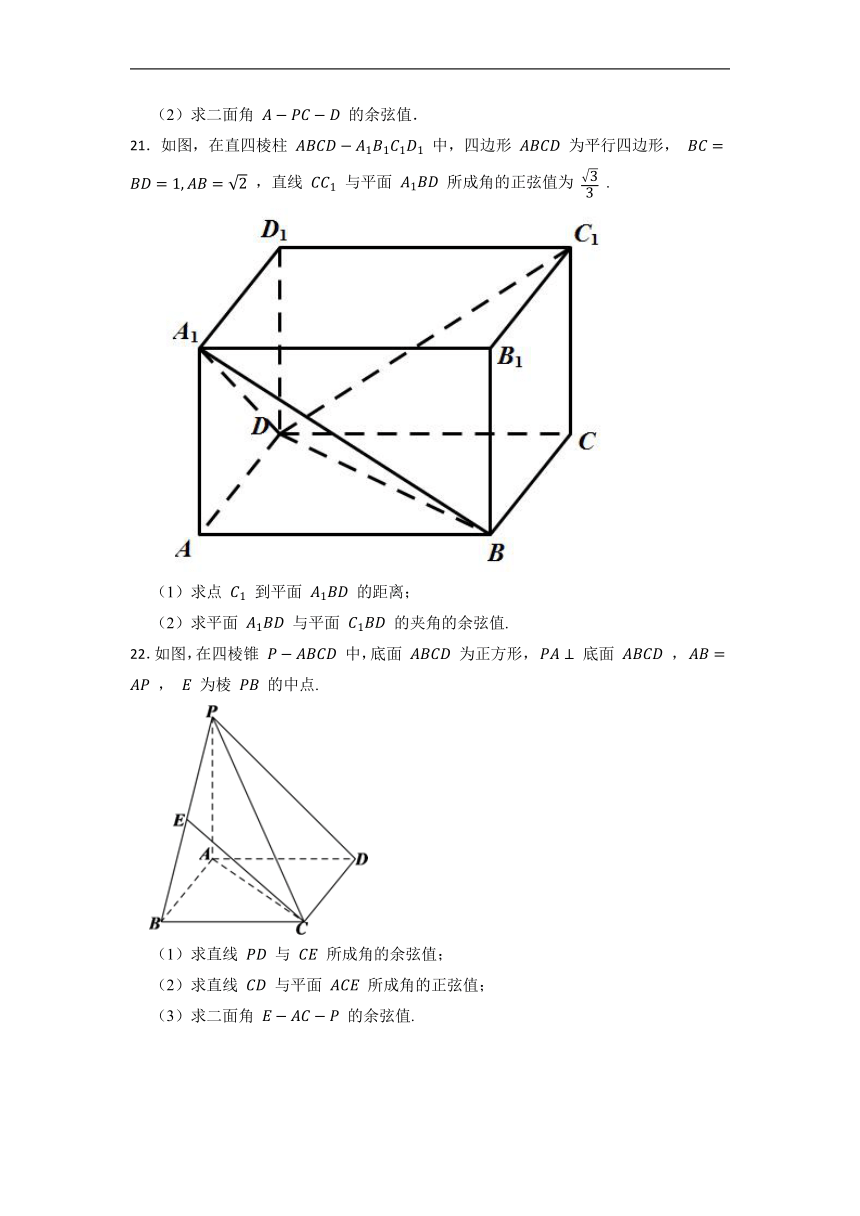
20.如图,在四棱锥 中,底面 为矩形, ⊥平面 ,
, 是棱 上一点,且 .
(1)求直线 与 所成角的余弦值;
(2)求二面角 的余弦值.
21.如图,在直四棱柱 中,四边形 为平行四边形, ,直线 与平面 所成角的正弦值为 .
(1)求点 到平面 的距离;
(2)求平面 与平面 的夹角的余弦值.
22.如图,在四棱锥 中,底面 为正方形, 底面 , , 为棱 的中点.
(1)求直线 与 所成角的余弦值;
(2)求直线 与平面 所成角的正弦值;
(3)求二面角 的余弦值.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B,D
10.【答案】B,C
11.【答案】A,B,D
12.【答案】A,B
13.【答案】
14.【答案】
15.【答案】3
16.【答案】
17.【答案】(1)证明:由题意,四边形 是矩形,可得 ,
又由 平面 , 平面 ,所以 ,
因为 ,所以 ,
又由 ,且 平面 ,所以 平面 ,
如图所示,以 为坐标原点,分别以 , , 所在的直线为 轴、 轴、 轴建立空间直角坐标系.
则 , , , , , .
由平面 的一个法向量为 ,
因为 ,即 ,即 ,
所以 平面
(2)解:由题意,得 , , , ,
平面 的一个法向量为 ,
设平面 的一个法向量 ,
可得 , ,
由 ,可得 ,即 ,
取 ,得 , ,所以 .
设二面角 的大小为 ,
则 .
所以二面角 的余弦值为
18.【答案】(1)解: , , , ,
,
设平面 的法向量 ,则
令 ,得平面 的一个法向量 ,
.
设平面 的法向量 ,则
令 ,得平面 的一个法向量 ,
设平面 与平面 的夹角为 ,
所以
(2)解:由(1)知,平面 的一个法向量 ,
,
设平面 与平面 的夹角为 ,
所以 ,
所以
19.【答案】(1)证明:以点 为原点,分别以 , , 所在直线为 轴, 轴, 轴建立坐标系,
不妨设 ,则 , , , , , .
设 ,则 , ,
∴ , ,
∵ ,∴ ,即 .
(2)解:由 ,得 , ,
∴ , , ,
设平面 的法向量 ,∵ , ,
由 ,得 ,令 ,得 , ,∴ ,
∵ 平面 ,∴平面 的法向量 ,
∴ ,所以二面角 的余弦值为 .
20.【答案】(1)解:以A为原点,AB为x轴,AD为y轴,AS为z轴,建立空间直角坐标系,
A(0,0,0),B(1,0,0),C(1,2,0),S(0,0,2),D(0,2,0),设P(a,b,c),
∵ ,∴(a,b,c﹣2)= (﹣a,2﹣b,﹣c)=(﹣ ,1﹣ ,﹣ ),
∴ ,解得a=0,b= ,c= ,∴P(0, , ),
=(1,0,0), =(﹣1,﹣ , ),
设直线AB与CP所成角为θ,
cosθ=|cos< >|= = = ,
∴直线AB与CP所成角的余弦值为
(2)解: =(1, ,﹣ ), =(0,﹣ ,﹣ ), =(0, ,﹣ ),
设平面APC的法向量 =(x,y,z),
则 ,取y=2,得 =(﹣4,2,﹣1),
设平面PCD的法向量 =(a,b,c),
则 ,取b=1,得 =(0,1,1),
设二面角A﹣PC﹣D的平面角为θ,
则cosθ= = = .
∴二面角A﹣PC﹣D的余弦值为 .
21.【答案】(1)解:因为 ,所以 ,所以
如图建立空间直角坐标系,
设 ,则
设平面 的法向量为
则 ,即 ,所以可取
所以 ,解得
所以 ,
所以点 到平面 的距离为
(2)解:设平面 的法向量为 ,
则 ,即 ,可取
所以 ,由图可得平面 与平面 的夹角为锐角
所以平面 与平面 的夹角的余弦值为
22.【答案】(1)解: 平面 ,四边形 为正方形,设 .
以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立空间直角坐标系,如下图所示:
则 、 、 、 、 、 .
, ,
,
所以,异面直线 、 所成角的余弦值为 ;
(2)解:设平面 的一个法向量为 , , ,
由 ,可得 ,取 ,可得 ,则 ,
, ,
因此,直线 与平面 所成角的正弦值为 ;
(3)解:设平面 的一个法向量为 , , ,
由 ,可得 ,得 ,取 ,则 , ,
所以,平面 的一个法向量为 ,
,
由图形可知,二面角 为锐角,
因此,二面角 的余弦值为 .
一、单选题
1.已知点 , ,则线段 的中点 的坐标为( )
A. B. C. D.
2.如果向量 , , 共面,则实数 的值是( )
A.-1 B.1 C.-5 D.5
3.已知O,A,B,C为空间不共面的四点,且向量 = ,向量 ,则不能与 构成空间的一个基底的是( )
A. B.
C. D. 或
4.已知向量 和 分别是直线 和 的方向向量,则直线 与 所成的角为( )
A. B. C. D.
5.若向量 , 且 与 的夹角余弦为 ,则λ等于( )
A. B. C. 或 D.2
6.如图,在空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,B1E1= A1B1,则 等于( )
A. B. C. D.
7.设 ,向量 , , ,且 , ,则 ( )
A. B.3 C. D.4
8.已知正四面体 的各棱长为1,点 是 的中点,则 的值为( )
A. B. C. D.
二、多选题
9.已知M(-1,1,3),N(-2,-1,4),若M,N,O三点共线,则O点坐标可能为( )
A.(3,5,-2) B.(-4,-5,6)
C.( , , ) D.(0,3,2)
10.空间直角坐标系中,下列说法正确的是( )
A.点 关于坐标平面 的对称点的坐标为
B.点 在平面 面上
C. 表示一个与坐标平面 平行的平面
D. 表示一条直线
11.在长方体 中, , ,以D为原点, , , 的方向分别为x轴,y轴,z轴正方向建立空间直角坐标系,则下列说法正确的是( )
A. 的坐标为(2,2,3)
B. =(-2,0,3)
C.平面 的一个法向量为(-3,3,-2)
D.二面角 的余弦值为
12.设动点 在正方体 的对角线 上,记 当 为钝角时,则实数可能的取值是( )
A. B. C. D.1
三、填空题
13.如图所示,在正方体 中,点 为线段 的中点,点 在线段 上移动,异面直线 与 所成角最小时,其余弦值为 .
14.如图,在三棱柱 中,所有棱长均为1,且 底面 ,则点 到平面 的距离为 .
15.如图,二面角 为 , , ,过 , 分别作 的垂线,垂足分别为 , ,若 , , ,则 的长度为 .
16.四棱锥 中, 底面ABCD,底面ABCD是正方形,且 , ,G是 的重心,则PG与面PAB所成角 的正弦值为 .
四、解答题
17.如图,在以 , , , , , 为顶点的多面体中,四边形 是矩形, , , 平面 , , .
(1)求证: 平面 ;
(2)求二面角 的余弦值.
18.如图,在空间直角坐标系中有直三棱柱 ,底面是等腰直角三角形, ,侧棱 分别是 的中点.
(1)求平面 与平面 的夹角的余弦.
(2)求 与平面 所成角的余弦值.
19.如图,在直三棱柱 中, , , , 分别是 和 上动点,且 .
(1)求证: ;
(2)若 ,求二面角 的平面角的余弦值.
20.如图,在四棱锥 中,底面 为矩形, ⊥平面 ,
, 是棱 上一点,且 .
(1)求直线 与 所成角的余弦值;
(2)求二面角 的余弦值.
21.如图,在直四棱柱 中,四边形 为平行四边形, ,直线 与平面 所成角的正弦值为 .
(1)求点 到平面 的距离;
(2)求平面 与平面 的夹角的余弦值.
22.如图,在四棱锥 中,底面 为正方形, 底面 , , 为棱 的中点.
(1)求直线 与 所成角的余弦值;
(2)求直线 与平面 所成角的正弦值;
(3)求二面角 的余弦值.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B,D
10.【答案】B,C
11.【答案】A,B,D
12.【答案】A,B
13.【答案】
14.【答案】
15.【答案】3
16.【答案】
17.【答案】(1)证明:由题意,四边形 是矩形,可得 ,
又由 平面 , 平面 ,所以 ,
因为 ,所以 ,
又由 ,且 平面 ,所以 平面 ,
如图所示,以 为坐标原点,分别以 , , 所在的直线为 轴、 轴、 轴建立空间直角坐标系.
则 , , , , , .
由平面 的一个法向量为 ,
因为 ,即 ,即 ,
所以 平面
(2)解:由题意,得 , , , ,
平面 的一个法向量为 ,
设平面 的一个法向量 ,
可得 , ,
由 ,可得 ,即 ,
取 ,得 , ,所以 .
设二面角 的大小为 ,
则 .
所以二面角 的余弦值为
18.【答案】(1)解: , , , ,
,
设平面 的法向量 ,则
令 ,得平面 的一个法向量 ,
.
设平面 的法向量 ,则
令 ,得平面 的一个法向量 ,
设平面 与平面 的夹角为 ,
所以
(2)解:由(1)知,平面 的一个法向量 ,
,
设平面 与平面 的夹角为 ,
所以 ,
所以
19.【答案】(1)证明:以点 为原点,分别以 , , 所在直线为 轴, 轴, 轴建立坐标系,
不妨设 ,则 , , , , , .
设 ,则 , ,
∴ , ,
∵ ,∴ ,即 .
(2)解:由 ,得 , ,
∴ , , ,
设平面 的法向量 ,∵ , ,
由 ,得 ,令 ,得 , ,∴ ,
∵ 平面 ,∴平面 的法向量 ,
∴ ,所以二面角 的余弦值为 .
20.【答案】(1)解:以A为原点,AB为x轴,AD为y轴,AS为z轴,建立空间直角坐标系,
A(0,0,0),B(1,0,0),C(1,2,0),S(0,0,2),D(0,2,0),设P(a,b,c),
∵ ,∴(a,b,c﹣2)= (﹣a,2﹣b,﹣c)=(﹣ ,1﹣ ,﹣ ),
∴ ,解得a=0,b= ,c= ,∴P(0, , ),
=(1,0,0), =(﹣1,﹣ , ),
设直线AB与CP所成角为θ,
cosθ=|cos< >|= = = ,
∴直线AB与CP所成角的余弦值为
(2)解: =(1, ,﹣ ), =(0,﹣ ,﹣ ), =(0, ,﹣ ),
设平面APC的法向量 =(x,y,z),
则 ,取y=2,得 =(﹣4,2,﹣1),
设平面PCD的法向量 =(a,b,c),
则 ,取b=1,得 =(0,1,1),
设二面角A﹣PC﹣D的平面角为θ,
则cosθ= = = .
∴二面角A﹣PC﹣D的余弦值为 .
21.【答案】(1)解:因为 ,所以 ,所以
如图建立空间直角坐标系,
设 ,则
设平面 的法向量为
则 ,即 ,所以可取
所以 ,解得
所以 ,
所以点 到平面 的距离为
(2)解:设平面 的法向量为 ,
则 ,即 ,可取
所以 ,由图可得平面 与平面 的夹角为锐角
所以平面 与平面 的夹角的余弦值为
22.【答案】(1)解: 平面 ,四边形 为正方形,设 .
以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立空间直角坐标系,如下图所示:
则 、 、 、 、 、 .
, ,
,
所以,异面直线 、 所成角的余弦值为 ;
(2)解:设平面 的一个法向量为 , , ,
由 ,可得 ,取 ,可得 ,则 ,
, ,
因此,直线 与平面 所成角的正弦值为 ;
(3)解:设平面 的一个法向量为 , , ,
由 ,可得 ,得 ,取 ,则 , ,
所以,平面 的一个法向量为 ,
,
由图形可知,二面角 为锐角,
因此,二面角 的余弦值为 .
