13.2.2 用坐标表示轴对称 课件(共22张PPT)
文档属性
| 名称 | 13.2.2 用坐标表示轴对称 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 14:42:44 | ||
图片预览







文档简介
(共22张PPT)
八上数学同步精品课件
人教版八年级上册
13.2.2 用坐标表示轴对称
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.(重点)
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.(重点)
3.能根据坐标系中轴对称点的坐标特点解决简单的问题.(难点)
一位外国游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
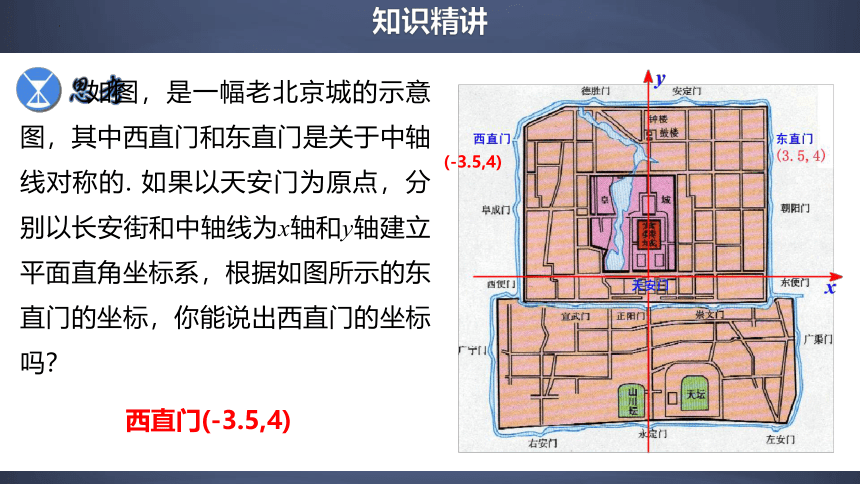
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的. 如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
西直门(-3.5,4)
(-3.5,4)
在平面直角坐标系中,画出以上列表中已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律.
A
B
C
D
E
A′
B′(-1,-2)
B′
A′(2,3)
C′
C′(-6,5)
D′
D′(,-1)
(E′)
E′(4,0)
A′′
A′′(-2,-3)
B′′
B′′(1,2)
C′′
C′′(6,-5)
D′′
D′′(-,1)
E′′
E′′(-4,0)
再找几个点,分别画出它们的对称点,检验一下你发现的规律.
在平面直角坐标系中,关于 x 轴对称的点横坐标_____,纵坐标___________;关于 y 轴对称的点横坐标___________,纵坐标_____.
点( x ,y )关于 x 轴对称的点的坐标为(___,___)
点( x ,y )关于 y 轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
例1.如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于 y 轴和 x 轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A、B、C、D关于y轴对称点的坐标分别为
A’(5,1),B’(2,1), C’(2,5),D’(5,4)
依次连接A'B',B'C',C'D',D'A',就可得到与四边形ABCD关于y轴对称的四边形A'B'C'D'.
类似地,我们可以得到与四边形ABCD关于x轴对称的四边形A″B″C″D″.
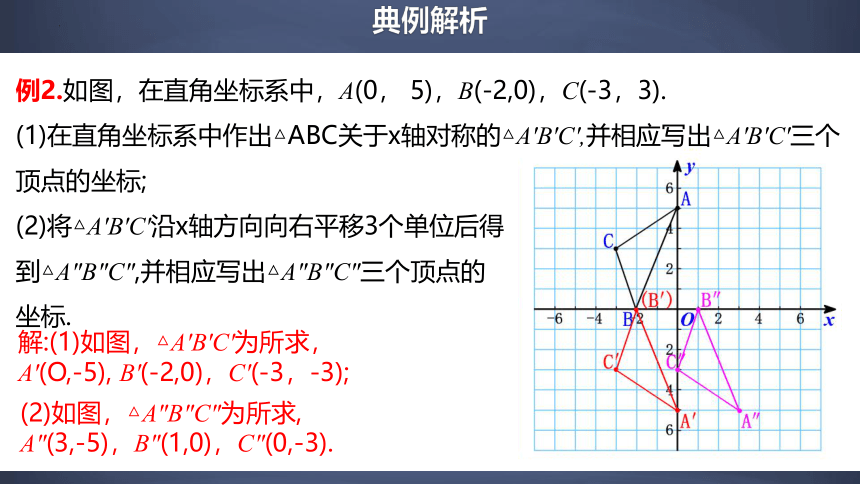
例2.如图,在直角坐标系中,A(0, 5),B(-2,0),C(-3,3).
(1)在直角坐标系中作出△ABC关于x轴对称的△A'B'C',并相应写出△A'B'C'三个顶点的坐标;
(2)将△A'B'C'沿x轴方向向右平移3个单位后得
到△A"B"C",并相应写出△A"B"C"三个顶点的
坐标.
解:(1)如图,△A'B'C'为所求,
A'(O,-5), B'(-2,0),C'(-3,-3);
(2)如图,△A"B"C"为所求,
A"(3,-5),B"(1,0),C"(0,-3).
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),
C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
解:如图所示:
例3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2016的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
典例解析
例4.已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a的取值范围.
解:依题意得P点在第四象限,
解得
即a的取值范围是
【点睛】解决此类题,一般先写出对称点的坐标或判断已知所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
1.若点P(-2, 3)与点Q关于x轴对称,则Q点的坐标是( )
A. (-2, 3) B. (2, 3) C. (-2,-3) D. (2,-3)
2.点M(1, 2)关于y轴对称的点的坐标是( )
A. (-1,2) B. (-1,-2) C. (1,-2) D. (2,-1)
3.已知点P关于x轴的对称点为(a,-2),关于y轴的对称点为(1,b),那么点P的坐标为( )
A. (a,-b) B. (b, -a) C. (-2, 1) D. (-1,2)
C
A
D
4.将平面直角坐标系内某个图形的各个点的横坐标都乘-1,纵坐标不变,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称 C.图形向左平移 D.图形向下平移
5.如图,x轴是△AOB的对称轴,y轴是△BOC的对称
轴,点A的坐标为(1,2),则点C的坐标为( )
A. (-1,-2) B. (1,-2)
C. (-1,2) D. (-2, 1)
B
A
6.点A(-3, 5)关于x轴对称的点的坐标是________,关于y轴对称的点的坐标是_________.
7.点B(5,-3)关于x轴对称的点的坐标是_________,关于y轴对称的点的坐标是__________.
8.若P(a, 3-b), Q(5, 2)关于x轴对称,则a=____,b=_____.
9.若M(3, 2),N(5-a, b)关于y轴对称,则a=____,b=_____.
10.横坐标不变,纵坐标分别乘以-1,则所得图形与原图形关于______对称.
11.已知点P (3, -1)关于y轴的对称点Q的坐标是(a+b, 1-b),则ab的值为_____.
(-3, -5)
(3, 5)
(5, 3)
(-5, -3)
5
5
8
2
25
x轴
12.在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出△ABC关于y轴对称的△A'B'C'; (其中A'、 B'、C'分别是A、B、C的对应点)
(2)直接写出A'、B'、C'三点的坐标: A' (_____)、 B'(_____)、C' (_____).
解: (1)△A'B'C'为所求.
2,3
3,1
-1,-2
13.若点C(-2,-3) 关于x轴的对称点为A,关于y轴的对称点为B,求△ABC的面积.
解:依题意,得A(-2, 3),B(2,-3).
如图,根据A、B、C三点坐标,可知△ABC为直角三角形,∠C=90°,BC=4,AC=6.
∴S△ABC=4×6=12.
14.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称变换,若原来点A坐标是(a, b),则经过第2022次变换后所得的A点坐标是_________.
(-a,-b)
在平面直角坐标系中,关于 x 轴对称的点横坐标_____,纵坐标___________;关于 y 轴对称的点横坐标___________,纵坐标_____.
点( x ,y )关于 x 轴对称的点的坐标为(___,___)
点( x ,y )关于 y 轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
13.2.2 用坐标表示轴对称
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.(重点)
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.(重点)
3.能根据坐标系中轴对称点的坐标特点解决简单的问题.(难点)
一位外国游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的. 如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
西直门(-3.5,4)
(-3.5,4)
在平面直角坐标系中,画出以上列表中已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律.
A
B
C
D
E
A′
B′(-1,-2)
B′
A′(2,3)
C′
C′(-6,5)
D′
D′(,-1)
(E′)
E′(4,0)
A′′
A′′(-2,-3)
B′′
B′′(1,2)
C′′
C′′(6,-5)
D′′
D′′(-,1)
E′′
E′′(-4,0)
再找几个点,分别画出它们的对称点,检验一下你发现的规律.
在平面直角坐标系中,关于 x 轴对称的点横坐标_____,纵坐标___________;关于 y 轴对称的点横坐标___________,纵坐标_____.
点( x ,y )关于 x 轴对称的点的坐标为(___,___)
点( x ,y )关于 y 轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
例1.如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于 y 轴和 x 轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A、B、C、D关于y轴对称点的坐标分别为
A’(5,1),B’(2,1), C’(2,5),D’(5,4)
依次连接A'B',B'C',C'D',D'A',就可得到与四边形ABCD关于y轴对称的四边形A'B'C'D'.
类似地,我们可以得到与四边形ABCD关于x轴对称的四边形A″B″C″D″.
例2.如图,在直角坐标系中,A(0, 5),B(-2,0),C(-3,3).
(1)在直角坐标系中作出△ABC关于x轴对称的△A'B'C',并相应写出△A'B'C'三个顶点的坐标;
(2)将△A'B'C'沿x轴方向向右平移3个单位后得
到△A"B"C",并相应写出△A"B"C"三个顶点的
坐标.
解:(1)如图,△A'B'C'为所求,
A'(O,-5), B'(-2,0),C'(-3,-3);
(2)如图,△A"B"C"为所求,
A"(3,-5),B"(1,0),C"(0,-3).
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),
C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
解:如图所示:
例3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2016的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
典例解析
例4.已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a的取值范围.
解:依题意得P点在第四象限,
解得
即a的取值范围是
【点睛】解决此类题,一般先写出对称点的坐标或判断已知所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
1.若点P(-2, 3)与点Q关于x轴对称,则Q点的坐标是( )
A. (-2, 3) B. (2, 3) C. (-2,-3) D. (2,-3)
2.点M(1, 2)关于y轴对称的点的坐标是( )
A. (-1,2) B. (-1,-2) C. (1,-2) D. (2,-1)
3.已知点P关于x轴的对称点为(a,-2),关于y轴的对称点为(1,b),那么点P的坐标为( )
A. (a,-b) B. (b, -a) C. (-2, 1) D. (-1,2)
C
A
D
4.将平面直角坐标系内某个图形的各个点的横坐标都乘-1,纵坐标不变,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称 C.图形向左平移 D.图形向下平移
5.如图,x轴是△AOB的对称轴,y轴是△BOC的对称
轴,点A的坐标为(1,2),则点C的坐标为( )
A. (-1,-2) B. (1,-2)
C. (-1,2) D. (-2, 1)
B
A
6.点A(-3, 5)关于x轴对称的点的坐标是________,关于y轴对称的点的坐标是_________.
7.点B(5,-3)关于x轴对称的点的坐标是_________,关于y轴对称的点的坐标是__________.
8.若P(a, 3-b), Q(5, 2)关于x轴对称,则a=____,b=_____.
9.若M(3, 2),N(5-a, b)关于y轴对称,则a=____,b=_____.
10.横坐标不变,纵坐标分别乘以-1,则所得图形与原图形关于______对称.
11.已知点P (3, -1)关于y轴的对称点Q的坐标是(a+b, 1-b),则ab的值为_____.
(-3, -5)
(3, 5)
(5, 3)
(-5, -3)
5
5
8
2
25
x轴
12.在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出△ABC关于y轴对称的△A'B'C'; (其中A'、 B'、C'分别是A、B、C的对应点)
(2)直接写出A'、B'、C'三点的坐标: A' (_____)、 B'(_____)、C' (_____).
解: (1)△A'B'C'为所求.
2,3
3,1
-1,-2
13.若点C(-2,-3) 关于x轴的对称点为A,关于y轴的对称点为B,求△ABC的面积.
解:依题意,得A(-2, 3),B(2,-3).
如图,根据A、B、C三点坐标,可知△ABC为直角三角形,∠C=90°,BC=4,AC=6.
∴S△ABC=4×6=12.
14.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称变换,若原来点A坐标是(a, b),则经过第2022次变换后所得的A点坐标是_________.
(-a,-b)
在平面直角坐标系中,关于 x 轴对称的点横坐标_____,纵坐标___________;关于 y 轴对称的点横坐标___________,纵坐标_____.
点( x ,y )关于 x 轴对称的点的坐标为(___,___)
点( x ,y )关于 y 轴对称的点的坐标为(___,___)
相等
互为相反数
互为相反数
相等
x -y
-x y
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
