广东省省实江门学校2022-2023学年高二上学期9月开学考试数学试题(含答案)
文档属性
| 名称 | 广东省省实江门学校2022-2023学年高二上学期9月开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 682.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 06:54:33 | ||
图片预览


文档简介
省实江门学校2022-2023学年第一学期开学考试
高二数学
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1.已知向量,则( )
A. B.2 C. D.50
2.设为平面内所有向量的一个基底,已知向量,若A,B,D三点共线,则k的值是( )
A.2 B.1 C. D.
3.在中,为边上的中线,E为的中点,则( )
A. B. C. D.
4.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )
A. B. C. D.
5.设m,n是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.如图所示,在三棱锥中,平面,且,点E为中点,则的长为( )
A. B.2 C. D.
7.刘徽(约公元225年-295年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形,当n变得很大时,这些等腰三角形的面积之和近似等于圆的面积运用割圆术的思想,得到的近似值为( )
A. B. C. D.
8.在三棱锥中,平面,D,E,F分别是棱的中点,,则直线与平面所成角的正弦值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形是平行四边形”
10.设向量,则( )
A. B.与的夹角是
C. D.与同向的单位向量是
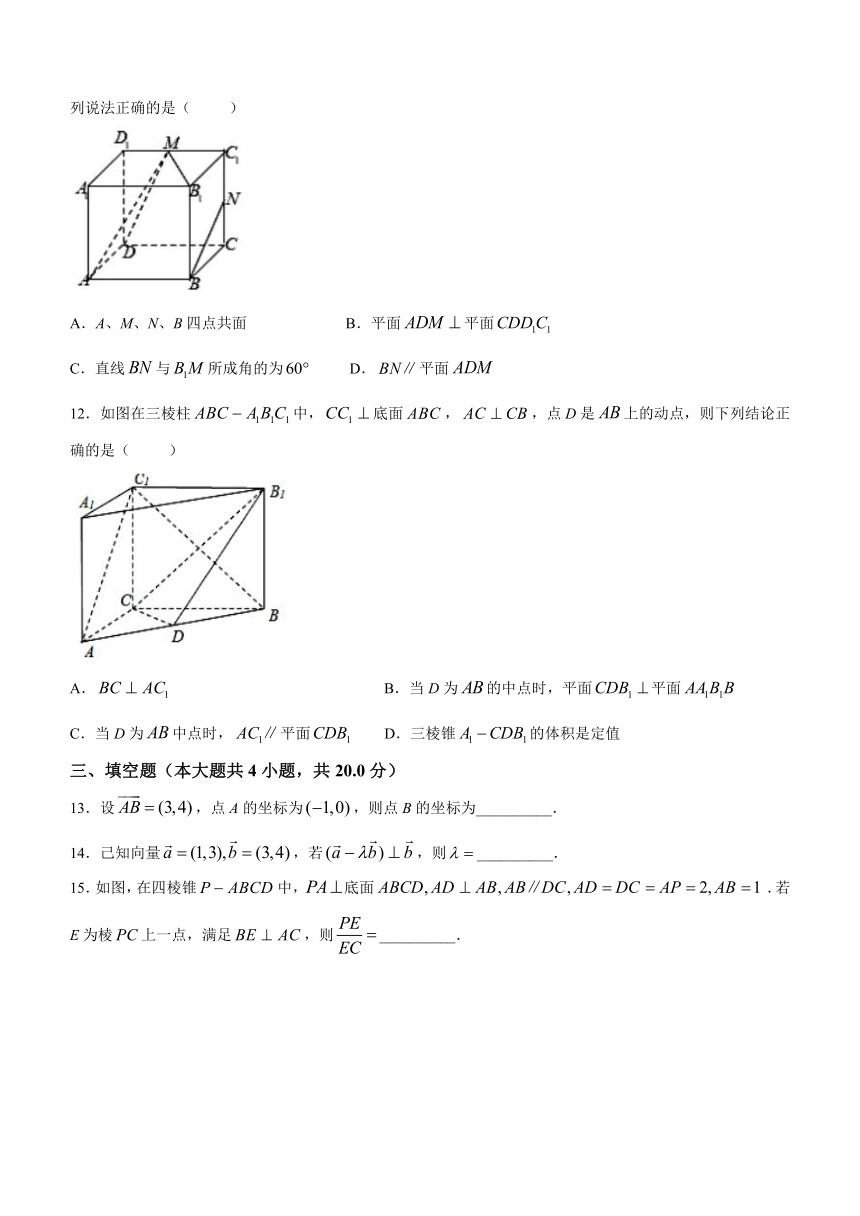
11.如图,在长方体中,,M,N分别为棱的中点,则下列说法正确的是( )
A.A、M、N、B四点共面 B.平面平面
C.直线与所成角的为 D.平面
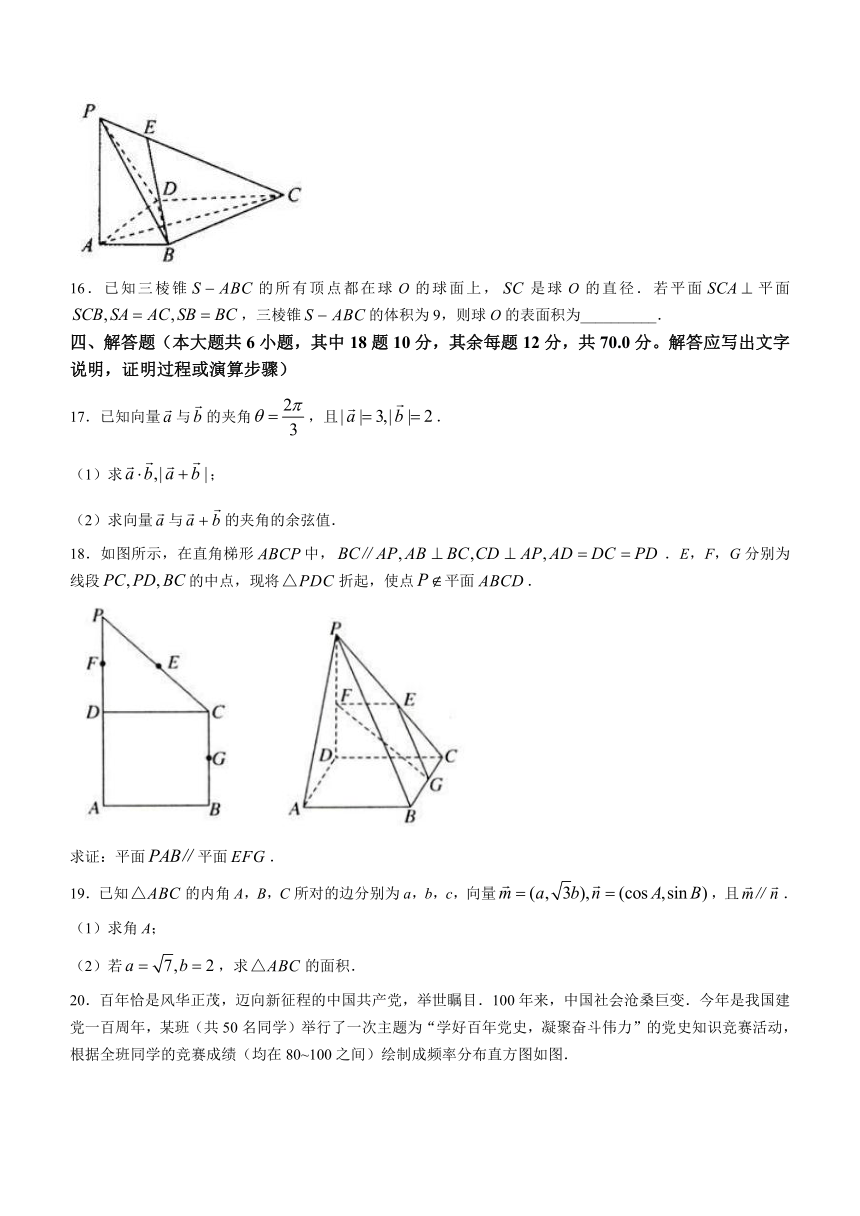
12.如图在三棱柱中,底面,,点D是上的动点,则下列结论正确的是( )
A. B.当D为的中点时,平面平面
C.当D为中点时,平面 D.三棱锥的体积是定值
三、填空题(本大题共4小题,共20.0分)
13.设,点A的坐标为,则点B的坐标为__________.
14.己知向量,若,则__________.
15.如图,在四棱锥中,底面.若E为棱上一点,满足,则__________.
16.已知三棱锥的所有顶点都在球O的球面上,是球O的直径.若平面平面,三棱锥的体积为9,则球O的表面积为__________.
四、解答题(本大题共6小题,其中18题10分,其余每题12分,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17.已知向量与的夹角,且.
(1)求;
(2)求向量与的夹角的余弦值.
18.如图所示,在直角梯形中,.E,F,G分别为线段的中点,现将折起,使点平面.
求证:平面平面.
19.已知的内角A,B,C所对的边分别为a,b,c,向量,且.
(1)求角A;
(2)若,求的面积.
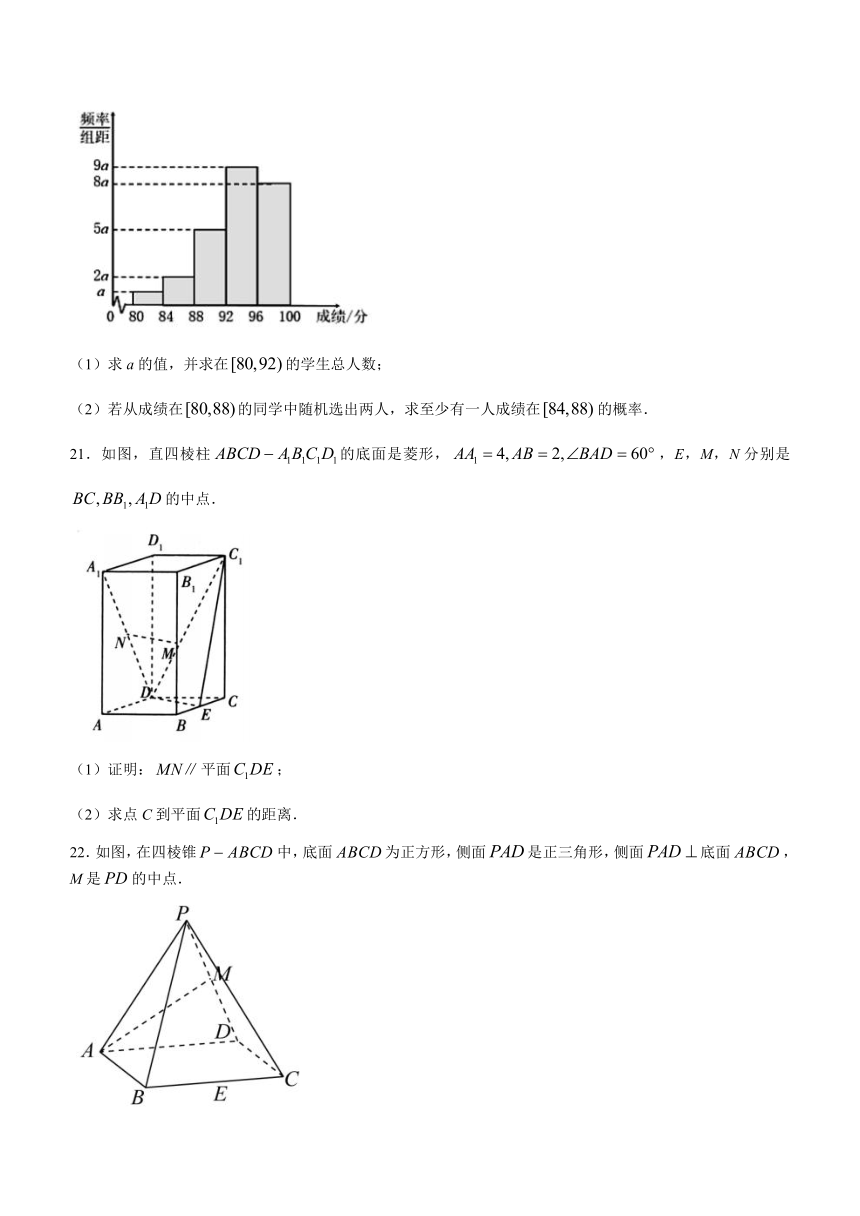
20.百年恰是风华正茂,迈向新征程的中国共产党,举世瞩目.100年来,中国社会沧桑巨变.今年是我国建党一百周年,某班(共50名同学)举行了一次主题为“学好百年党史,凝聚奋斗伟力”的党史知识竞赛活动,根据全班同学的竞赛成绩(均在80~100之间)绘制成频率分布直方图如图.
(1)求a的值,并求在的学生总人数;
(2)若从成绩在的同学中随机选出两人,求至少有一人成绩在的概率.
21.如图,直四棱柱的底面是菱形,,E,M,N分别是的中点.
(1)证明:平面;
(2)求点C到平面的距离.
22.如图,在四棱锥中,底面为正方形,侧面是正三角形,侧面底面,M是的中点.
(1)求证:平面;
(2)求侧面与底面所成二面角的余弦值.
省实江门学校2022-2023学年第一学期开学考试
高二数学参考答案
1.A 2.D 3.A 4.C 5.B 6.C 7.B 8.B 9.AD 10.BC 11.BC 12.ACD
13. 14. 15. 16.
17.解:(1),
,
(2)设向量与的夹角,
则.
18.证明:∵,
∴,
又∵,
∴.
又平面,
∴平面.
同理可证平面.
又∵平面,
∴平面平面.
19.解:(1)因为,所以.
由正弦定理,得,
因为,所以.
又A为的内角,
所以.
(2)由余弦定理,得,即,
解得或(舍去),
所以的面积.
20.解:(1)由,解得,
其中在内有2人,在内有4人,在内有10人,共有16人;
(2)其中在内有2人,在内有4人,
设此六人分别为A,B和c,d,e,f,
则从成绩在的同学中随机选出2位,有,;;;共15种可能情形,
记“至少有一人成绩在”为事件C,
事件C包含;;;;14种情况,
故,
答:至少有一人成绩在的概率为
21.解:(1)连接.
因为M,E分别为的中点,
所以,且,
又因为N为的中点,
所以,
由题设知,可得,
故,
因此四边形为平行四边形,.
又平面平面,
所以平面.
(2)过C作的垂线,垂足为H,
由已知可得,
所以平面,故,
从而平面,
故的长即为C到平面的距离,
由已知可得,
所以,故,
从而点C到平面的距离为.
22.(1)证明:∵平面平面,交线为,
又底面为正方形,平面,
∴平面,
又平面,∴,
又是正三角形,M是的中点,
∴.
又平面,
∴平面.
(2)取、的中点分别为E、F,连接、、.
由(1)知平面,得平面,
∵平面,
∴,即,而,
∴,
∴,E为的中点,
∴,
又,
∴为侧面与底面所成的二面角,且,
设正方形边长为a,可求得,∴,
∴,
即侧面与底面所成二面角的余弦值为.
高二数学
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1.已知向量,则( )
A. B.2 C. D.50
2.设为平面内所有向量的一个基底,已知向量,若A,B,D三点共线,则k的值是( )
A.2 B.1 C. D.
3.在中,为边上的中线,E为的中点,则( )
A. B. C. D.
4.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )
A. B. C. D.
5.设m,n是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.如图所示,在三棱锥中,平面,且,点E为中点,则的长为( )
A. B.2 C. D.
7.刘徽(约公元225年-295年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形,当n变得很大时,这些等腰三角形的面积之和近似等于圆的面积运用割圆术的思想,得到的近似值为( )
A. B. C. D.
8.在三棱锥中,平面,D,E,F分别是棱的中点,,则直线与平面所成角的正弦值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形是平行四边形”
10.设向量,则( )
A. B.与的夹角是
C. D.与同向的单位向量是
11.如图,在长方体中,,M,N分别为棱的中点,则下列说法正确的是( )
A.A、M、N、B四点共面 B.平面平面
C.直线与所成角的为 D.平面
12.如图在三棱柱中,底面,,点D是上的动点,则下列结论正确的是( )
A. B.当D为的中点时,平面平面
C.当D为中点时,平面 D.三棱锥的体积是定值
三、填空题(本大题共4小题,共20.0分)
13.设,点A的坐标为,则点B的坐标为__________.
14.己知向量,若,则__________.
15.如图,在四棱锥中,底面.若E为棱上一点,满足,则__________.
16.已知三棱锥的所有顶点都在球O的球面上,是球O的直径.若平面平面,三棱锥的体积为9,则球O的表面积为__________.
四、解答题(本大题共6小题,其中18题10分,其余每题12分,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17.已知向量与的夹角,且.
(1)求;
(2)求向量与的夹角的余弦值.
18.如图所示,在直角梯形中,.E,F,G分别为线段的中点,现将折起,使点平面.
求证:平面平面.
19.已知的内角A,B,C所对的边分别为a,b,c,向量,且.
(1)求角A;
(2)若,求的面积.
20.百年恰是风华正茂,迈向新征程的中国共产党,举世瞩目.100年来,中国社会沧桑巨变.今年是我国建党一百周年,某班(共50名同学)举行了一次主题为“学好百年党史,凝聚奋斗伟力”的党史知识竞赛活动,根据全班同学的竞赛成绩(均在80~100之间)绘制成频率分布直方图如图.
(1)求a的值,并求在的学生总人数;
(2)若从成绩在的同学中随机选出两人,求至少有一人成绩在的概率.
21.如图,直四棱柱的底面是菱形,,E,M,N分别是的中点.
(1)证明:平面;
(2)求点C到平面的距离.
22.如图,在四棱锥中,底面为正方形,侧面是正三角形,侧面底面,M是的中点.
(1)求证:平面;
(2)求侧面与底面所成二面角的余弦值.
省实江门学校2022-2023学年第一学期开学考试
高二数学参考答案
1.A 2.D 3.A 4.C 5.B 6.C 7.B 8.B 9.AD 10.BC 11.BC 12.ACD
13. 14. 15. 16.
17.解:(1),
,
(2)设向量与的夹角,
则.
18.证明:∵,
∴,
又∵,
∴.
又平面,
∴平面.
同理可证平面.
又∵平面,
∴平面平面.
19.解:(1)因为,所以.
由正弦定理,得,
因为,所以.
又A为的内角,
所以.
(2)由余弦定理,得,即,
解得或(舍去),
所以的面积.
20.解:(1)由,解得,
其中在内有2人,在内有4人,在内有10人,共有16人;
(2)其中在内有2人,在内有4人,
设此六人分别为A,B和c,d,e,f,
则从成绩在的同学中随机选出2位,有,;;;共15种可能情形,
记“至少有一人成绩在”为事件C,
事件C包含;;;;14种情况,
故,
答:至少有一人成绩在的概率为
21.解:(1)连接.
因为M,E分别为的中点,
所以,且,
又因为N为的中点,
所以,
由题设知,可得,
故,
因此四边形为平行四边形,.
又平面平面,
所以平面.
(2)过C作的垂线,垂足为H,
由已知可得,
所以平面,故,
从而平面,
故的长即为C到平面的距离,
由已知可得,
所以,故,
从而点C到平面的距离为.
22.(1)证明:∵平面平面,交线为,
又底面为正方形,平面,
∴平面,
又平面,∴,
又是正三角形,M是的中点,
∴.
又平面,
∴平面.
(2)取、的中点分别为E、F,连接、、.
由(1)知平面,得平面,
∵平面,
∴,即,而,
∴,
∴,E为的中点,
∴,
又,
∴为侧面与底面所成的二面角,且,
设正方形边长为a,可求得,∴,
∴,
即侧面与底面所成二面角的余弦值为.
同课章节目录
