广东省省实江门学校2022-2023学年高一上学期9月开学考试数学试题(含答案)
文档属性
| 名称 | 广东省省实江门学校2022-2023学年高一上学期9月开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 06:55:19 | ||
图片预览

文档简介
省实江门学校2022-2023学年第一学期开学考试
高一数学试卷
本试卷分选择题和非选择题两部分,共4页,满分120分,考试用时90分钟.
第一部分 选择题(共30分)
一、选择题(本大题10小题,每小题3分,共30分)
1.2022的相反数是( )
A.2022 B. C. D.
2.随着科技不断发展,芯片的集成度越来越高,我国企业中芯国际已经实现14纳米量产,14纳米=0.000014.
毫米,0.000014用科学记数法表示为( )
A. B. C. D.
3.现在道路上的车辆是越来越多了,如果没有交通规则约束和交通标志指示,那么路上的车辆一定是混杂堵塞,所以开车时一定要看清标志,文明驾车.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列运算正确是( )
A. B. C. D.
5.一个几何体由若干大小相同的小立方木块搭成,如图是它的主视图和俯视图,那么搭成该几何体所需小立方木块的个数最少为( )
A.6 B.5 C.4 D.3
6.在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )
A.7,9 B.9,9 C.9,8 D.8,9
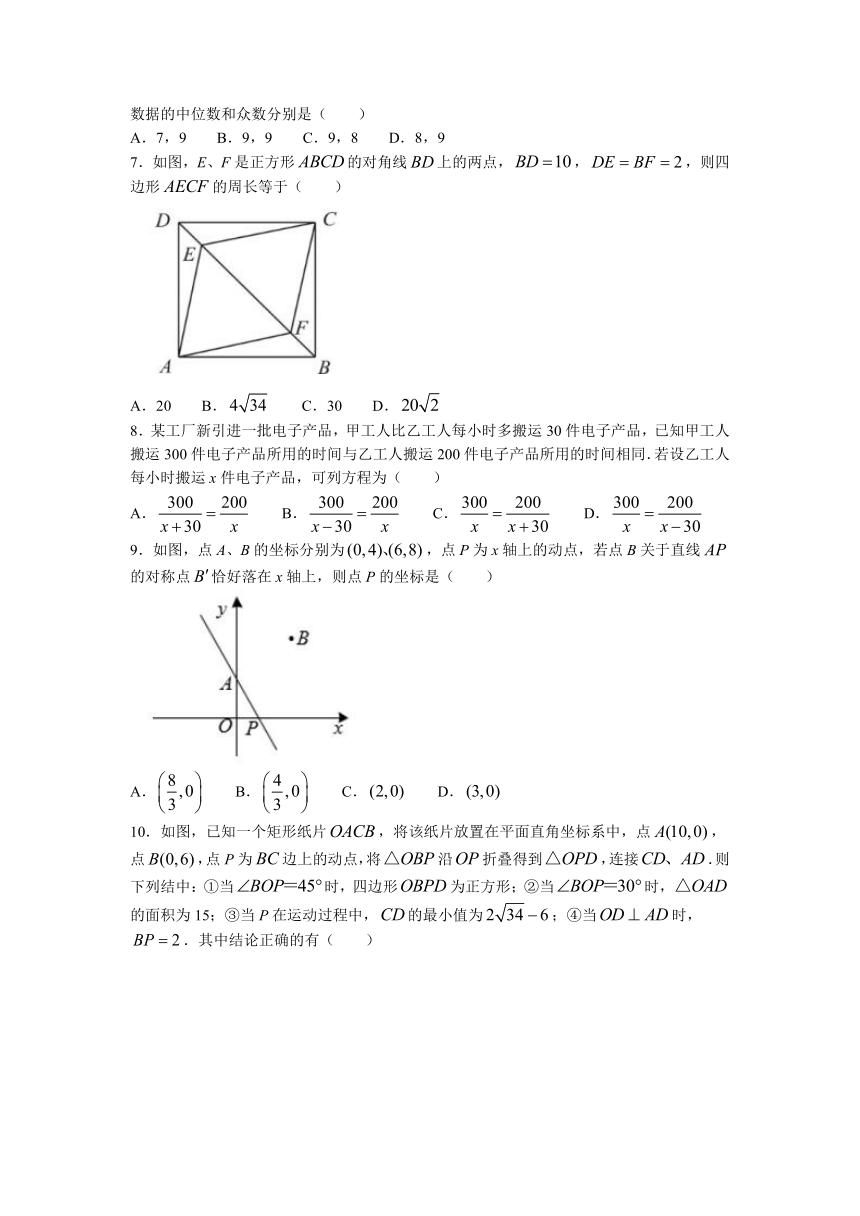
7.如图,E、F是正方形的对角线上的两点,,,则四边形的周长等于( )
A.20 B. C.30 D.
8.某工厂新引进一批电子产品,甲工人比乙工人每小时多搬运30件电子产品,已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同.若设乙工人每小时搬运x件电子产品,可列方程为( )
A. B. C. D.
9.如图,点A、B的坐标分别为,点P为x轴上的动点,若点B关于直线的对称点恰好落在x轴上,则点P的坐标是( )
A. B. C. D.
10.如图,已知一个矩形纸片,将该纸片放置在平面直角坐标系中,点,点,点P为边上的动点,将沿折叠得到,连接.则下列结中:①当时,四边形为正方形;②当时,的面积为15;③当P在运动过程中,的最小值为;④当时,.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
第二部分 非选择题(共90分)
二、填空题(本大题5小题,每小题3分,共15分)
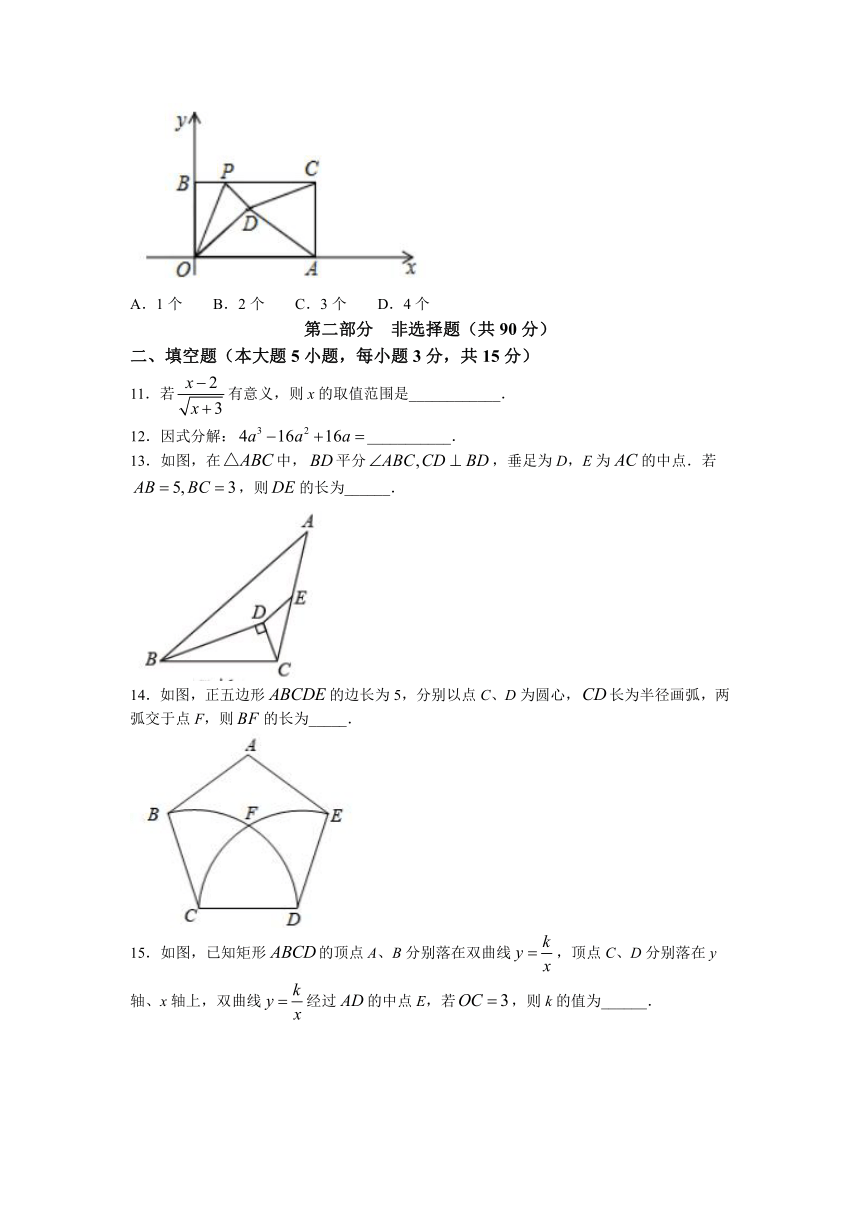
11.若有意义,则x的取值范围是____________.
12.因式分解:___________.
13.如图,在中,平分,垂足为D,E为的中点.若,则的长为______.
14.如图,正五边形的边长为5,分别以点C、D为圆心,长为半径画弧,两弧交于点F,则的长为_____.
15.如图,已知矩形的顶点A、B分别落在双曲线,顶点C、D分别落在y轴、x轴上,双曲线经过的中点E,若,则k的值为______.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.解不等式组.
17.先化简,再求值:,其中.
18.如图,四边形中,,与相交于点O,,求证:四边形是平行四边形.
四、解答题(二)(本大题3小题,每小题9分,共27分)
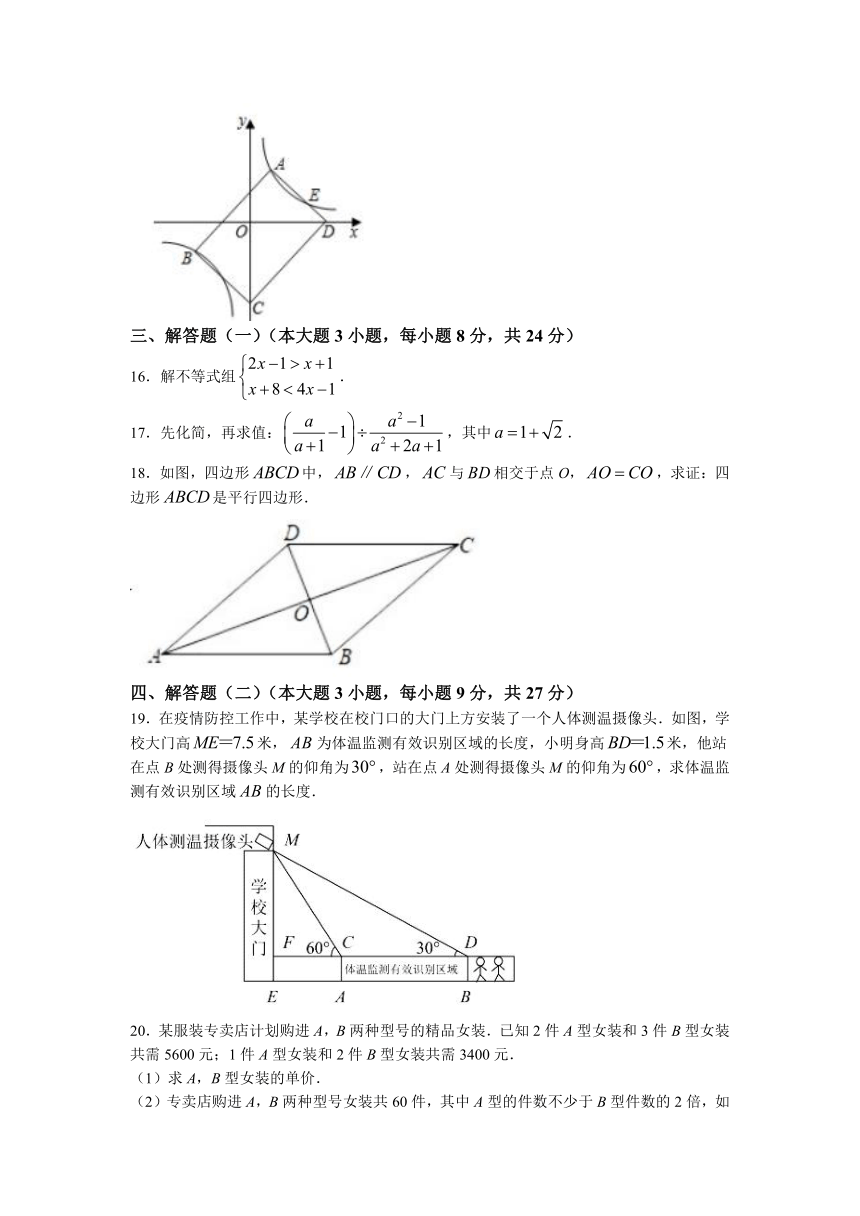
19.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高米,为体温监测有效识别区域的长度,小明身高米,他站在点B处测得摄像头M的仰角为,站在点A处测得摄像头M的仰角为,求体温监测有效识别区域的长度.
20.某服装专卖店计划购进A,B两种型号的精品女装.已知2件A型女装和3件B型女装共需5600元;1件A型女装和2件B型女装共需3400元.
(1)求A,B型女装的单价.
(2)专卖店购进A,B两种型号女装共60件,其中A型的件数不少于B型件数的2倍,如果B型女装打八折,那么该专卖店至少需要准备多少贷款?
21.某学校课后服务,为学生们提供了手工烹饪,文学赏析,体育锻炼,编导表演四种课程(依次用A,B,C,D表示),为了解学生对这四种课程的将好情况:学校随机抽取部分学生进行了“你最喜欢哪一种课外活动(必选且只选一种)”的问卷调查,并根据调查结果绘制了条形统计图和扇形统计图,部分信息如图:
(1)参加问卷调查的学生人数是__________人,扇形统计图中“D”对应扇形的圆心角的大小为________.
(2)估计全体1000名学生中最喜欢C活动的人数约为多少人?
(3)现从喜好编导表演甲、乙、丙、丁四名学生中任选两人搭档彩排双人相声,请用树状图或列表法求恰好甲和丁同学被选到的概率是多少?
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.如图,四边形内接于,为直径,和交于点E,.
(1)求的度数;
(2)过B作的平行线,交于F,试判断线段,,之间满足的等量关系,并说明理由;
(3)在(2)条件下过E,F分别作,的垂线,垂足分别为G,H,连接,交于M,若,求的半径.
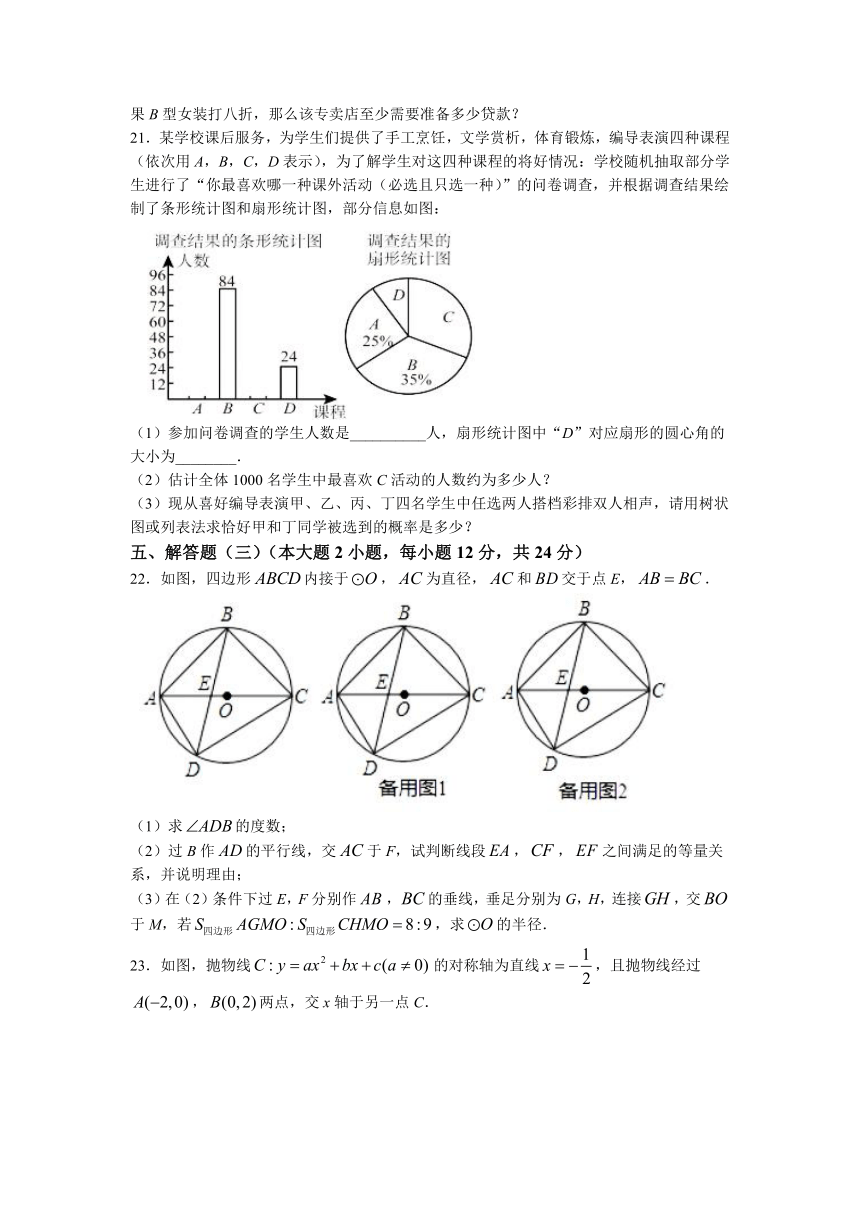
23.如图,抛物线的对称轴为直线,且抛物线经过,两点,交x轴于另一点C.
(1)求抛物线的解析式;
(2)过点A作直线的垂线交y轴于点D,平移直线交抛物线于点E,F两点,连结,.若为以为斜边的直角三角形,求平移后的直线的解析式.
(3)设对称轴直线与x轴交于M,点P为抛物线上对称轴左侧一点,直线交抛物线于另一点Q,点P关于抛物线对称轴对称点H,直线交抛物线对称轴于G点,在点P运动过程中长是否为一定值,若为定值,请求出其值,若不为定值,请求出其变化范围.
省实江门学校2022-2023学年第一学期开学考试
高一数学参考答案
一、选择题(每题3分,10小题,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C D B A A D
部分题目说明
7、解:如图,连接,与相交于点O,
∵四边形是正方形,
∴,
∴
∵,
∴,
在中,
∵
∴四边形是平行四边形
∵
∴四边形是菱形,
∴
∴四边形的周长
9、解:如图,连接、,
∵,
∴,
∵点B与关于直线对称,
∴,
在中,
∴点坐标为或,
∵,点关于直线的对称点恰好落在x轴上,
∴点关于直线的对称点,
∴点坐标为不合题意舍去,
设直线方程为
将代入得:,
解得,
∴直线的解析式为:,
∴直线的解析式为:,
当时,,
解得:,
∴点P的坐标为:;
故选:A.
10、解:①∵四边形是矩形,
∴,
∵将沿折叠得到,
∴,,,
∵,
∴,
∴,
∴,
∴四边形是矩形,
∵,
∴四边形为正方形:故①正确:
②过D作于H,
∵点,点,
∴,
∴,
∴,
∴,
∴的面积为,故②正确;
③连接,
则,
即当时,取最小值,
∵,
∴,
∴,
即的最小值为;故③正确;
④∵,
∴,
∵,
∴,
∴P,D,A三点共线,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故④正确;
二、填空题(每题3分,5小题,共15分)
11、 12、 13、1 14、 15、2
部分题目详解
13、解:延长交于F,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
14、解:连接,,
则是等边三角形,
∴,
在正五边形中,,
∴,
∴的长,
故答案为:.
15、解:设A点坐标为,则,如图,
过点A作轴于点M,过点B作轴于点N,过点E作轴于点F,
∵四边形是矩形,
∴,,,
∵,
∴,
∵,
∵,
在和中,
,
∴,
∴,,
∵,
∴,即,且B在图象上,
∴,
∴,
∵点E是的中点,
∴,
∴,
∵双曲线经过的中点E,
∴,解得,
∴,
而,且矩形有,
∴,
解得或(舍去),
∴,代入得:.
三、解答题(共8小题,共75分)
16、解;,
由①得,,
由②得,,
故此不等式组的解集为:.
17、解:原式
当时,
原式
18、证明:∵,
∴
在和中,
,
∴,
∴,
∵.
∴四边形是平行四边形.
19、解:根据题意可知:四边形和是矩形,米,
∴米,,
设,
在中,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
解得:,
∴(米).
答:体温监测有效识别区域的长为米.
20、解:(1)设A型女装单价为x元,B型女装单价为y元.
根据题意可得
解得
所以A型女装的单价是1000元,B型女装的单价是1200元.
(2)设该专卖店购进A型女装x(,且x为整数)件,则购进B型女装件.
根据题意可得.
解得.
∴,且x为整数.
设该专卖店需要准备贷款y元.
根据题意可得.
∵,
∴y随x的增大而增大.
∴当时,y有最小值为元.
∴该专卖店至少需要准备59200元的贷款.
21、解:(1)由条形统计图和扇形统计图可知参加问卷调查的学生人数是人;
“D”对应的人数为24人,对应扇形的圆心角大小.
(2)最喜欢D活动的人数占总调查人数:,
∴最喜欢C活动的人数占总调查人数:,
∴1000名学生中最喜欢C活动的人数约有:人.
(3)树状图如下:
恰好选到甲和丁同学有2种情况,总的情况有12种,
∴恰好选到甲和丁同学的概率为.
22、解:解:(1)如图1,
∵为直径,
∴,
∴,
∵,
∴,
∴;
(2)线段,,之间满足的等量关系为:.理由如下:
如图2,设,,
∵,
∴,
又,
∴,
过B作,使,连接,
∵,,,
∴,
∴,,
∴.
∵,,,
∴,
∴,
∵在中,,
∴;
(3)如图3,延长交于K,
由(2)知,
∴,
∴,
∴,
即,
∴,
∴,
∴,
∴,
∵平分,
∴,
设,,
∴,
∵,
∴,
∴,
∴∵,
∴,
整理得:,
解得:(舍去),.
∴,
∴,
∴的半径为,
23、解:(1)∵的对称轴为直线,
∴.
又在抛物线上C上,
∴
∴抛物线上C的解析式为.
(2)∵抛物线上C的解析式为的对称轴,
∴.
∵,
∴直线的解析式.
∴直线的斜率为,解析式.
设直线的解析式,
∵,
∴.
∵为以为斜边的直角三角形,
∴.
∵,,
∴,即,
整理得,解得或,
∴平移后的直线的解析式为或,
(3)∵抛物线上C的解析式为,对称轴直线与x轴交于点M,
∴.
设直线的解析式为,
∵直线交抛物线于另一点Q,点P关于抛物线对称轴对称点H,
∴,∴,
.
设,
∵斜率,
∴,
整理得,,
∴.
高一数学试卷
本试卷分选择题和非选择题两部分,共4页,满分120分,考试用时90分钟.
第一部分 选择题(共30分)
一、选择题(本大题10小题,每小题3分,共30分)
1.2022的相反数是( )
A.2022 B. C. D.
2.随着科技不断发展,芯片的集成度越来越高,我国企业中芯国际已经实现14纳米量产,14纳米=0.000014.
毫米,0.000014用科学记数法表示为( )
A. B. C. D.
3.现在道路上的车辆是越来越多了,如果没有交通规则约束和交通标志指示,那么路上的车辆一定是混杂堵塞,所以开车时一定要看清标志,文明驾车.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列运算正确是( )
A. B. C. D.
5.一个几何体由若干大小相同的小立方木块搭成,如图是它的主视图和俯视图,那么搭成该几何体所需小立方木块的个数最少为( )
A.6 B.5 C.4 D.3
6.在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )
A.7,9 B.9,9 C.9,8 D.8,9
7.如图,E、F是正方形的对角线上的两点,,,则四边形的周长等于( )
A.20 B. C.30 D.
8.某工厂新引进一批电子产品,甲工人比乙工人每小时多搬运30件电子产品,已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同.若设乙工人每小时搬运x件电子产品,可列方程为( )
A. B. C. D.
9.如图,点A、B的坐标分别为,点P为x轴上的动点,若点B关于直线的对称点恰好落在x轴上,则点P的坐标是( )
A. B. C. D.
10.如图,已知一个矩形纸片,将该纸片放置在平面直角坐标系中,点,点,点P为边上的动点,将沿折叠得到,连接.则下列结中:①当时,四边形为正方形;②当时,的面积为15;③当P在运动过程中,的最小值为;④当时,.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
第二部分 非选择题(共90分)
二、填空题(本大题5小题,每小题3分,共15分)
11.若有意义,则x的取值范围是____________.
12.因式分解:___________.
13.如图,在中,平分,垂足为D,E为的中点.若,则的长为______.
14.如图,正五边形的边长为5,分别以点C、D为圆心,长为半径画弧,两弧交于点F,则的长为_____.
15.如图,已知矩形的顶点A、B分别落在双曲线,顶点C、D分别落在y轴、x轴上,双曲线经过的中点E,若,则k的值为______.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.解不等式组.
17.先化简,再求值:,其中.
18.如图,四边形中,,与相交于点O,,求证:四边形是平行四边形.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高米,为体温监测有效识别区域的长度,小明身高米,他站在点B处测得摄像头M的仰角为,站在点A处测得摄像头M的仰角为,求体温监测有效识别区域的长度.
20.某服装专卖店计划购进A,B两种型号的精品女装.已知2件A型女装和3件B型女装共需5600元;1件A型女装和2件B型女装共需3400元.
(1)求A,B型女装的单价.
(2)专卖店购进A,B两种型号女装共60件,其中A型的件数不少于B型件数的2倍,如果B型女装打八折,那么该专卖店至少需要准备多少贷款?
21.某学校课后服务,为学生们提供了手工烹饪,文学赏析,体育锻炼,编导表演四种课程(依次用A,B,C,D表示),为了解学生对这四种课程的将好情况:学校随机抽取部分学生进行了“你最喜欢哪一种课外活动(必选且只选一种)”的问卷调查,并根据调查结果绘制了条形统计图和扇形统计图,部分信息如图:
(1)参加问卷调查的学生人数是__________人,扇形统计图中“D”对应扇形的圆心角的大小为________.
(2)估计全体1000名学生中最喜欢C活动的人数约为多少人?
(3)现从喜好编导表演甲、乙、丙、丁四名学生中任选两人搭档彩排双人相声,请用树状图或列表法求恰好甲和丁同学被选到的概率是多少?
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.如图,四边形内接于,为直径,和交于点E,.
(1)求的度数;
(2)过B作的平行线,交于F,试判断线段,,之间满足的等量关系,并说明理由;
(3)在(2)条件下过E,F分别作,的垂线,垂足分别为G,H,连接,交于M,若,求的半径.
23.如图,抛物线的对称轴为直线,且抛物线经过,两点,交x轴于另一点C.
(1)求抛物线的解析式;
(2)过点A作直线的垂线交y轴于点D,平移直线交抛物线于点E,F两点,连结,.若为以为斜边的直角三角形,求平移后的直线的解析式.
(3)设对称轴直线与x轴交于M,点P为抛物线上对称轴左侧一点,直线交抛物线于另一点Q,点P关于抛物线对称轴对称点H,直线交抛物线对称轴于G点,在点P运动过程中长是否为一定值,若为定值,请求出其值,若不为定值,请求出其变化范围.
省实江门学校2022-2023学年第一学期开学考试
高一数学参考答案
一、选择题(每题3分,10小题,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C D B A A D
部分题目说明
7、解:如图,连接,与相交于点O,
∵四边形是正方形,
∴,
∴
∵,
∴,
在中,
∵
∴四边形是平行四边形
∵
∴四边形是菱形,
∴
∴四边形的周长
9、解:如图,连接、,
∵,
∴,
∵点B与关于直线对称,
∴,
在中,
∴点坐标为或,
∵,点关于直线的对称点恰好落在x轴上,
∴点关于直线的对称点,
∴点坐标为不合题意舍去,
设直线方程为
将代入得:,
解得,
∴直线的解析式为:,
∴直线的解析式为:,
当时,,
解得:,
∴点P的坐标为:;
故选:A.
10、解:①∵四边形是矩形,
∴,
∵将沿折叠得到,
∴,,,
∵,
∴,
∴,
∴,
∴四边形是矩形,
∵,
∴四边形为正方形:故①正确:
②过D作于H,
∵点,点,
∴,
∴,
∴,
∴,
∴的面积为,故②正确;
③连接,
则,
即当时,取最小值,
∵,
∴,
∴,
即的最小值为;故③正确;
④∵,
∴,
∵,
∴,
∴P,D,A三点共线,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故④正确;
二、填空题(每题3分,5小题,共15分)
11、 12、 13、1 14、 15、2
部分题目详解
13、解:延长交于F,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
14、解:连接,,
则是等边三角形,
∴,
在正五边形中,,
∴,
∴的长,
故答案为:.
15、解:设A点坐标为,则,如图,
过点A作轴于点M,过点B作轴于点N,过点E作轴于点F,
∵四边形是矩形,
∴,,,
∵,
∴,
∵,
∵,
在和中,
,
∴,
∴,,
∵,
∴,即,且B在图象上,
∴,
∴,
∵点E是的中点,
∴,
∴,
∵双曲线经过的中点E,
∴,解得,
∴,
而,且矩形有,
∴,
解得或(舍去),
∴,代入得:.
三、解答题(共8小题,共75分)
16、解;,
由①得,,
由②得,,
故此不等式组的解集为:.
17、解:原式
当时,
原式
18、证明:∵,
∴
在和中,
,
∴,
∴,
∵.
∴四边形是平行四边形.
19、解:根据题意可知:四边形和是矩形,米,
∴米,,
设,
在中,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
解得:,
∴(米).
答:体温监测有效识别区域的长为米.
20、解:(1)设A型女装单价为x元,B型女装单价为y元.
根据题意可得
解得
所以A型女装的单价是1000元,B型女装的单价是1200元.
(2)设该专卖店购进A型女装x(,且x为整数)件,则购进B型女装件.
根据题意可得.
解得.
∴,且x为整数.
设该专卖店需要准备贷款y元.
根据题意可得.
∵,
∴y随x的增大而增大.
∴当时,y有最小值为元.
∴该专卖店至少需要准备59200元的贷款.
21、解:(1)由条形统计图和扇形统计图可知参加问卷调查的学生人数是人;
“D”对应的人数为24人,对应扇形的圆心角大小.
(2)最喜欢D活动的人数占总调查人数:,
∴最喜欢C活动的人数占总调查人数:,
∴1000名学生中最喜欢C活动的人数约有:人.
(3)树状图如下:
恰好选到甲和丁同学有2种情况,总的情况有12种,
∴恰好选到甲和丁同学的概率为.
22、解:解:(1)如图1,
∵为直径,
∴,
∴,
∵,
∴,
∴;
(2)线段,,之间满足的等量关系为:.理由如下:
如图2,设,,
∵,
∴,
又,
∴,
过B作,使,连接,
∵,,,
∴,
∴,,
∴.
∵,,,
∴,
∴,
∵在中,,
∴;
(3)如图3,延长交于K,
由(2)知,
∴,
∴,
∴,
即,
∴,
∴,
∴,
∴,
∵平分,
∴,
设,,
∴,
∵,
∴,
∴,
∴∵,
∴,
整理得:,
解得:(舍去),.
∴,
∴,
∴的半径为,
23、解:(1)∵的对称轴为直线,
∴.
又在抛物线上C上,
∴
∴抛物线上C的解析式为.
(2)∵抛物线上C的解析式为的对称轴,
∴.
∵,
∴直线的解析式.
∴直线的斜率为,解析式.
设直线的解析式,
∵,
∴.
∵为以为斜边的直角三角形,
∴.
∵,,
∴,即,
整理得,解得或,
∴平移后的直线的解析式为或,
(3)∵抛物线上C的解析式为,对称轴直线与x轴交于点M,
∴.
设直线的解析式为,
∵直线交抛物线于另一点Q,点P关于抛物线对称轴对称点H,
∴,∴,
.
设,
∵斜率,
∴,
整理得,,
∴.
同课章节目录
