第五单元数学广角抽屉原理(课件)六年级下册数学人教版(共14张PPT)
文档属性
| 名称 | 第五单元数学广角抽屉原理(课件)六年级下册数学人教版(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 168.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 05:52:12 | ||
图片预览


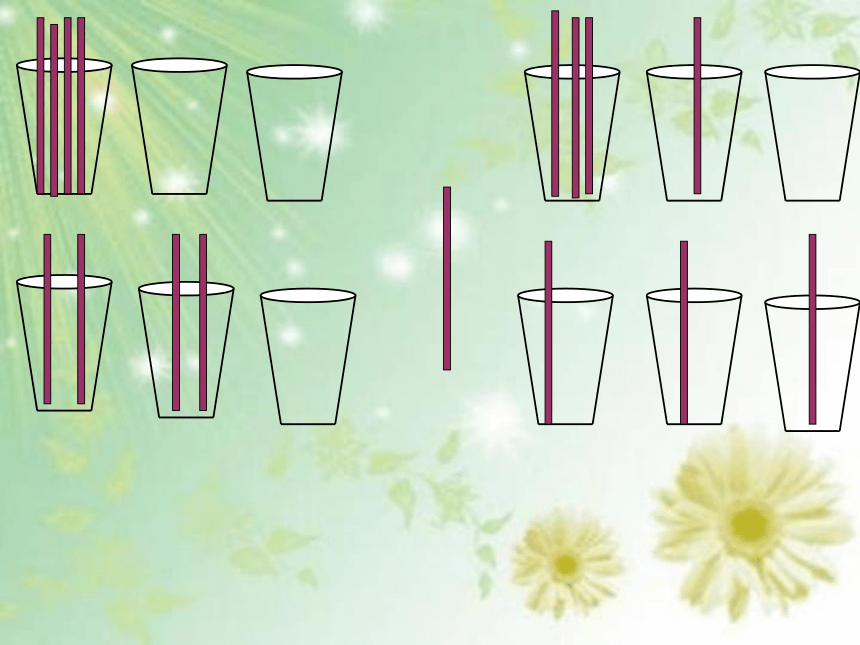



文档简介
(共14张PPT)
鸽巢问题
把4支笔放进3个杯子里,有哪几种放法?总有一个杯子里至少有几支笔?
温馨提示:1.所有的笔都必须放进杯子里,不考虑杯子的顺序,只考虑杯子内的支数。(可以有空杯子)
2.想一想,怎样放才能做到既不重复,也不遗漏?
3小组合作,把分法用你们喜欢的方式记录下来。如(4,0,0)或
至少
总有
把4支笔放进3个杯子里,不管怎么放,总有一个杯子至少有2支笔
想一想:有没有最直接的方法,只摆一种情况,就能得到结论?
如果每个杯子里放1支笔,
剩下的( )支笔,
所以,总有一个杯子里至少放( )支笔。
3
1
2
还要放进其中一个杯子里,
最多放( )支笔,
5支笔放入4个杯子里,总有一个杯子至少有几支笔?
6支笔放入5个杯子里,总有一个杯子至少有几支笔?
100支笔放入99个杯子里,总有一个杯子至少有几支笔?
.....
5÷4=1.....1
6÷5=1.....1
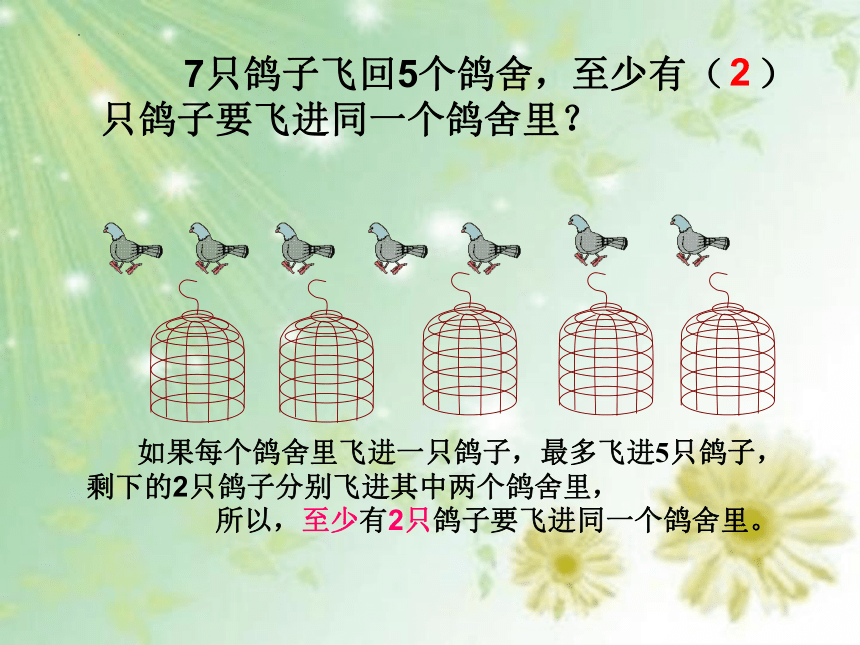
如果每个鸽舍里飞进一只鸽子,最多飞进5只鸽子,
7只鸽子飞回5个鸽舍,至少有( )只鸽子要飞进同一个鸽舍里?
剩下的2只鸽子分别飞进其中两个鸽舍里,
所以,至少有2只鸽子要飞进同一个鸽舍里。
2
数学小知识:鸽巢原理的由来。
最先发现这一规律的人是19世纪的德国数学家狄里克雷,后人为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又叫“鸽巢原理”,还把它叫做 “抽屉原理”。
视频
只要物体数量是抽屉数量的1倍多,总有一个抽屉里至少放进2个的物体。
鸽巢原理
物体数÷抽屉数=商......余数
至少数=商+1
鸽巢问题计算绝招
1.为什么3个人中一定至少有2个人是同性别的?
2.为什么在任意的13人中一定至少有2个人在同一月过生日?
想:把什么当作抽屉,把什么当作要分的物体?
智勇大冲关
第一关:稳中求胜
第二关:激流勇进
3、一副扑克去掉大王、小王后还剩52张,
抽出5张,至少有 张是统一花色的?
5÷4=1(张) …… 1(张)
1 + 1 = 2(张)
2
在我们班的任意20人中,至少有 个人的属相相同,想一想,为什么?
20÷12=1(人)……8(人)
1 + 1 =2(人)
2
第三关:勇攀高峰
说说这节课你有什么收获?
鸽巢问题
把4支笔放进3个杯子里,有哪几种放法?总有一个杯子里至少有几支笔?
温馨提示:1.所有的笔都必须放进杯子里,不考虑杯子的顺序,只考虑杯子内的支数。(可以有空杯子)
2.想一想,怎样放才能做到既不重复,也不遗漏?
3小组合作,把分法用你们喜欢的方式记录下来。如(4,0,0)或
至少
总有
把4支笔放进3个杯子里,不管怎么放,总有一个杯子至少有2支笔
想一想:有没有最直接的方法,只摆一种情况,就能得到结论?
如果每个杯子里放1支笔,
剩下的( )支笔,
所以,总有一个杯子里至少放( )支笔。
3
1
2
还要放进其中一个杯子里,
最多放( )支笔,
5支笔放入4个杯子里,总有一个杯子至少有几支笔?
6支笔放入5个杯子里,总有一个杯子至少有几支笔?
100支笔放入99个杯子里,总有一个杯子至少有几支笔?
.....
5÷4=1.....1
6÷5=1.....1
如果每个鸽舍里飞进一只鸽子,最多飞进5只鸽子,
7只鸽子飞回5个鸽舍,至少有( )只鸽子要飞进同一个鸽舍里?
剩下的2只鸽子分别飞进其中两个鸽舍里,
所以,至少有2只鸽子要飞进同一个鸽舍里。
2
数学小知识:鸽巢原理的由来。
最先发现这一规律的人是19世纪的德国数学家狄里克雷,后人为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又叫“鸽巢原理”,还把它叫做 “抽屉原理”。
视频
只要物体数量是抽屉数量的1倍多,总有一个抽屉里至少放进2个的物体。
鸽巢原理
物体数÷抽屉数=商......余数
至少数=商+1
鸽巢问题计算绝招
1.为什么3个人中一定至少有2个人是同性别的?
2.为什么在任意的13人中一定至少有2个人在同一月过生日?
想:把什么当作抽屉,把什么当作要分的物体?
智勇大冲关
第一关:稳中求胜
第二关:激流勇进
3、一副扑克去掉大王、小王后还剩52张,
抽出5张,至少有 张是统一花色的?
5÷4=1(张) …… 1(张)
1 + 1 = 2(张)
2
在我们班的任意20人中,至少有 个人的属相相同,想一想,为什么?
20÷12=1(人)……8(人)
1 + 1 =2(人)
2
第三关:勇攀高峰
说说这节课你有什么收获?
