13.1.2 线段的垂直平分线的性质 第1课时 课件(共20张PPT)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质 第1课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 08:44:21 | ||
图片预览




文档简介
(共20张PPT)
线段的垂直平分线的性质
13.1.2 线段的垂直平分线的性质
| 第1课时|
13.1.2 线段的垂直平分线的性质(第1课时)
理解并掌握线段的垂直平分线的性质和判定方法.
会用尺规过一点作已知直线的垂线.
能够运用线段的垂直平分线的性质和判定解决实际问题
情景引入
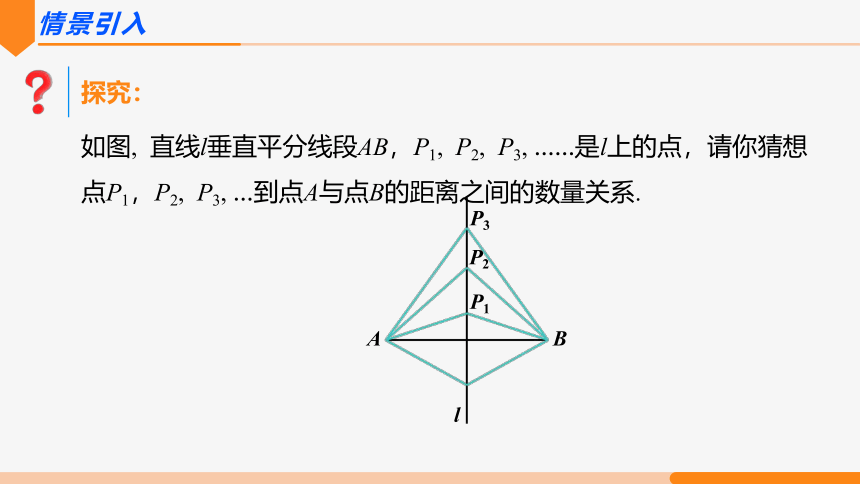
探究:
A
B
l
P1
P2
P3
如图, 直线l垂直平分线段AB,P1, P2, P3, ……是l上的点,请你猜想点P1,P2, P3, …到点A与点B的距离之间的数量关系.
猜想:线段垂直平分线上的点和这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
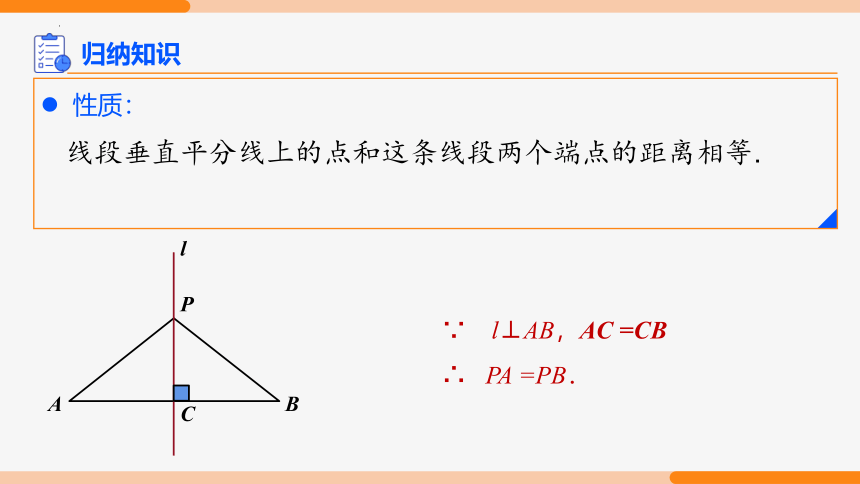
性质:
线段垂直平分线上的点和这条线段两个端点的距离相等.
归纳知识
P
A
B
l
C
∵ l⊥AB,AC =CB
∴ PA =PB.
针对练习
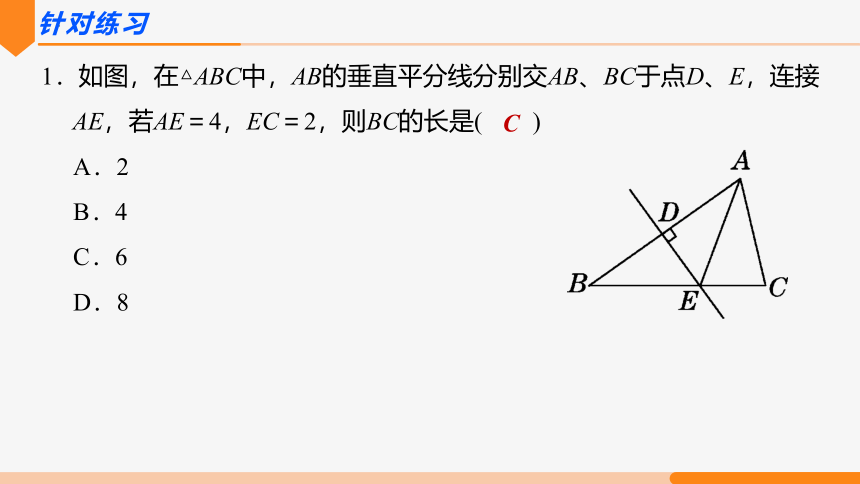
1.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
C
思考:
如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
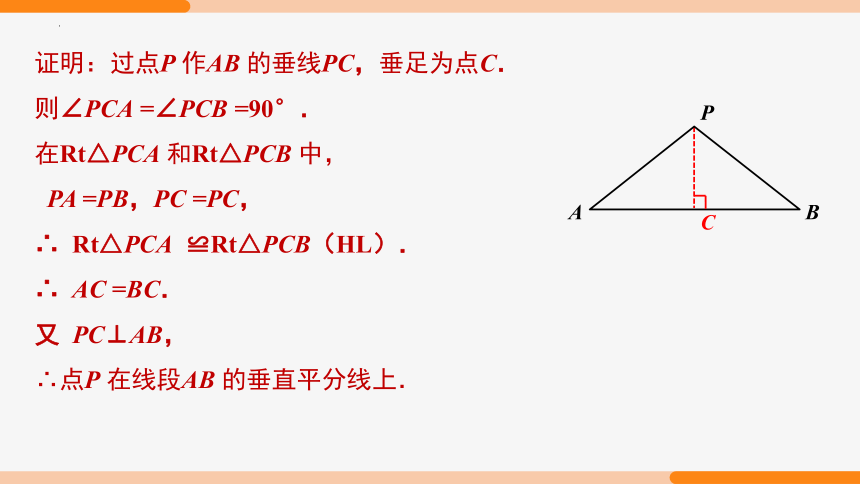
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
C
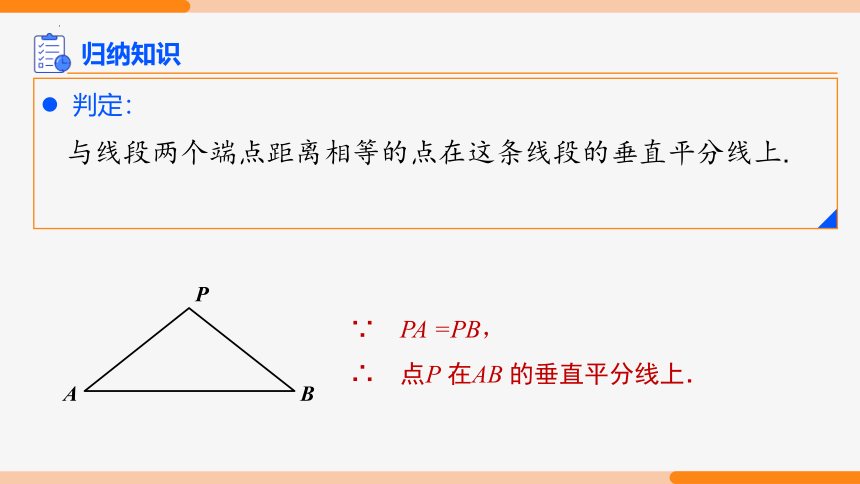
判定:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
归纳知识
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
探究:
能找到多少个到线段AB 两端点距离相等的点?这些点能组成什么几何图形?
P
A
B
C
l
典例讲解
例1 如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm
B.10 cm
C.15 cm
D.17.5 cm
C
利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
归纳知识
例2. 已知:如图,在△ABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
证明:∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理,PB=PC.
∴PA=PB=PC.
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
归纳知识
例3. 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
课堂小结
线段的
垂直平分线
性质
判定
知垂直平分线,得线段相等
互逆
知线段相等,得点在垂直平分线
集合定义线段
垂直平分线
课堂练习
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8 cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18 cm,则AC的长是 .
B
10 cm
P
A
B
C
D
图①
A
B
C
D
E
图②
3.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD
B .CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
A
B
C
D
A
4.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16 cm,则△BCE的周长是 cm.
A
B
C
D
E
16
6.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解 AD垂直平分EF.
∵ AD平分∠BAC,DE⊥AB,DF⊥AC,
∴ ∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵ AD=AD,
∴ △ADE≌△ADF,
∴ AE=AF,DE=DF.
∴ A、D均在线段EF的垂直平分线上,
即直线AD垂直平分线段EF.
A
B
C
D
E
F
7.如图,在四边形ADBC中,AB与CD互相垂直平分,垂足为点O.
(1)找出图中相等的线段;
(2)若OE,OF分别是点O到∠CAD两边的垂线段,试说明它们的大小有什么关系.
解:(1)∵AB、CD互相垂直平分,
∴OC=OD,AO=OB,
且AC=BC=AD=BD.
(2)OE=OF.理由如下:
在△AOC和△AOD中,
∵AC=AD,AO=AO,OC=OD,
∴△AOC≌△AOD(SSS),
∴∠CAO=∠DAO.
又∵OE⊥AC,OF⊥AD,
∴OE=OF.
线段的垂直平分线的性质
13.1.2 线段的垂直平分线的性质
| 第1课时|
13.1.2 线段的垂直平分线的性质(第1课时)
理解并掌握线段的垂直平分线的性质和判定方法.
会用尺规过一点作已知直线的垂线.
能够运用线段的垂直平分线的性质和判定解决实际问题
情景引入
探究:
A
B
l
P1
P2
P3
如图, 直线l垂直平分线段AB,P1, P2, P3, ……是l上的点,请你猜想点P1,P2, P3, …到点A与点B的距离之间的数量关系.
猜想:线段垂直平分线上的点和这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
性质:
线段垂直平分线上的点和这条线段两个端点的距离相等.
归纳知识
P
A
B
l
C
∵ l⊥AB,AC =CB
∴ PA =PB.
针对练习
1.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
C
思考:
如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
C
判定:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
归纳知识
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
探究:
能找到多少个到线段AB 两端点距离相等的点?这些点能组成什么几何图形?
P
A
B
C
l
典例讲解
例1 如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm
B.10 cm
C.15 cm
D.17.5 cm
C
利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
归纳知识
例2. 已知:如图,在△ABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
证明:∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理,PB=PC.
∴PA=PB=PC.
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
归纳知识
例3. 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
课堂小结
线段的
垂直平分线
性质
判定
知垂直平分线,得线段相等
互逆
知线段相等,得点在垂直平分线
集合定义线段
垂直平分线
课堂练习
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8 cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18 cm,则AC的长是 .
B
10 cm
P
A
B
C
D
图①
A
B
C
D
E
图②
3.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD
B .CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
A
B
C
D
A
4.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16 cm,则△BCE的周长是 cm.
A
B
C
D
E
16
6.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解 AD垂直平分EF.
∵ AD平分∠BAC,DE⊥AB,DF⊥AC,
∴ ∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵ AD=AD,
∴ △ADE≌△ADF,
∴ AE=AF,DE=DF.
∴ A、D均在线段EF的垂直平分线上,
即直线AD垂直平分线段EF.
A
B
C
D
E
F
7.如图,在四边形ADBC中,AB与CD互相垂直平分,垂足为点O.
(1)找出图中相等的线段;
(2)若OE,OF分别是点O到∠CAD两边的垂线段,试说明它们的大小有什么关系.
解:(1)∵AB、CD互相垂直平分,
∴OC=OD,AO=OB,
且AC=BC=AD=BD.
(2)OE=OF.理由如下:
在△AOC和△AOD中,
∵AC=AD,AO=AO,OC=OD,
∴△AOC≌△AOD(SSS),
∴∠CAO=∠DAO.
又∵OE⊥AC,OF⊥AD,
∴OE=OF.
