24.1.3 弧、弦、圆心角 课件(共17张PPT)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 11:56:41 | ||
图片预览




文档简介
(共17张PPT)
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.3 弧、弦、圆心角
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
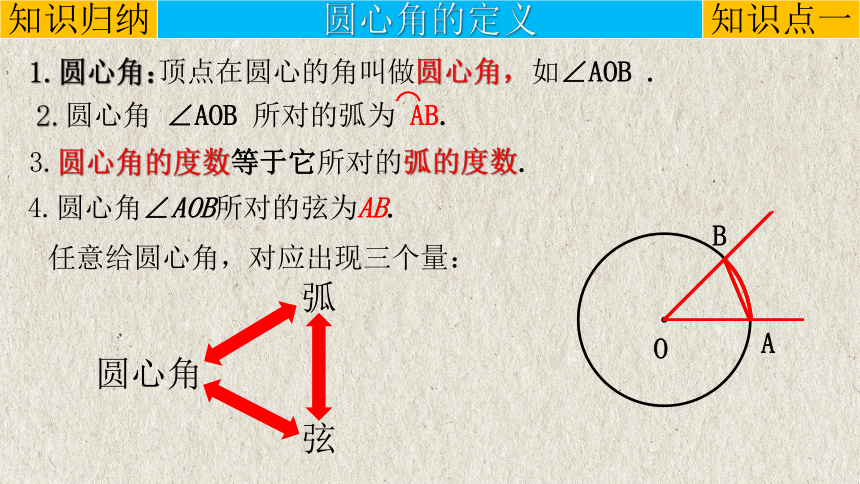
1.圆心角:
顶点在圆心的角叫做圆心角,如∠AOB .
O
A
B
4.圆心角∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
弦
3.圆心角的度数等于它所对的弧的度数.
知识点一
知识归纳
圆心角的定义
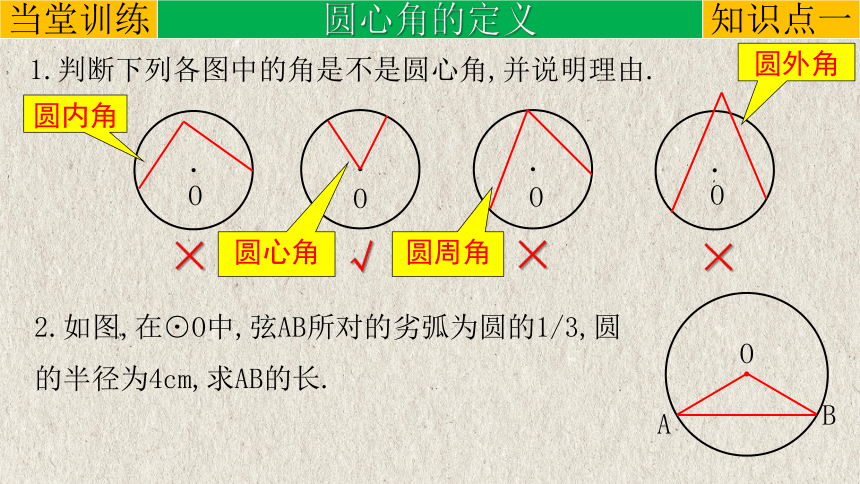
1.判断下列各图中的角是不是圆心角,并说明理由.
O
O
O
O
×
√
×
×
圆内角
圆心角
圆周角
圆外角
A
B
O
2.如图,在⊙O中,弦AB所对的劣弧为圆的1/3,圆的半径为4cm,求AB的长.
知识点一
当堂训练
圆心角的定义
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
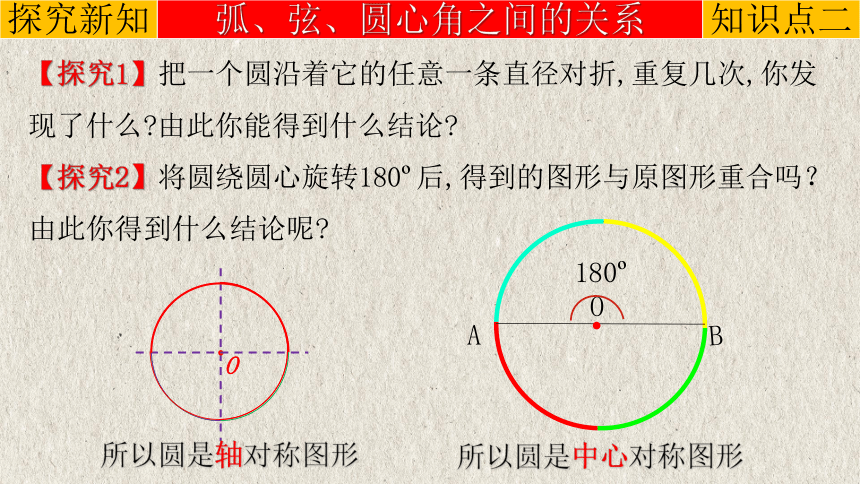
【探究1】把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么 由此你能得到什么结论
【探究2】将圆绕圆心旋转180 后,得到的图形与原图形重合吗?由此你得到什么结论呢
O
所以圆是轴对称图形
O
A
B
180
所以圆是中心对称图形
知识点二
探究新知
弧、弦、圆心角之间的关系
【探究3】把圆绕圆心旋转任意一个角度呢 仍与原来的圆重合吗.
O
α
·
圆既是轴对称图形,
又是中心对称图形,
还具有旋转不变性。
由圆的轴对称性质得出---垂径定理。
由圆的旋转不变性可得出什么结论?
知识点二
探究新知
弧、弦、圆心角之间的关系
【在同圆中探究】在⊙O中,当圆心角∠AOB=∠A OB 时,它们所对的弧AB和弧A B ,弦AB和弦A B 相等吗?
O
A
B
A
B
AB=A B ,弧AB=弧A B
在同圆中∠AOB=∠A OB
知识点二
探究新知
弧、弦、圆心角之间的关系
条件:
结论:
【在等圆中探究】在等圆中,若∠AOB=∠A O B ,你发现的等量关系是否依然成立?
O
A
B
·
O
A
B
·
·
AB=A B ,弧AB=弧A B
在等圆中∠AOB=∠A OB
知识点二
探究新知
弧、弦、圆心角之间的关系
条件:
结论:
圆心角
相等
弧相等
弦相等
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角、弧、弦之间的关系定理:
思
考
举例说明:为什么要说“在同圆或等圆中”?
A
B
O
D
C
知识点二
知识归纳
弧、弦、圆心角之间的关系
小林根据在圆心角、弧、弦三个量之间的关系,认为在如图中,若∠AOB=2∠COD,则有AB=2CD,AB=2CD,你同意他的观点吗?试说明你的理由.
⌒
⌒
A
D
C
O
B
E
知识点二
当堂训练
弧、弦、圆心角之间的关系
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
【探究1】在同圆或等圆中,如果两条弧相等,能得到什么结论?
【探究2】在同圆或等圆中,如果两条弦相等,能得到什么结论?
O
A
B
A
B
结论:∠AOB=∠A OB ,弧AB=弧A B
条件:在同圆或等圆中AB=A B
结论:AB=A B ,∠AOB=∠A OB ,
条件:在同圆或等圆中弧AB=弧A B
归纳:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
知识点三
探究新知
关系定理的推论
证明:
又∵∠ACB=60 ,
∴△ABC是等边三角形,AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
【例1】如图在⊙O中,AB=AC,∠ACB=60 ,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
∵AB=AC
⌒
⌒
·
B
C
O
A
∴AB=AC,△ABC等腰三角形.
知识点三
典例精讲
关系定理的推论
×
√
×
1.判断下列说法是否正确.
(1)相等的圆心角所对的弧相等. ( )
(2)等弧所对的弦相等. ( )
(3)相等的弦所对的弧相等. ( )
2.弦长等于半径的弦所对的圆心角等于 .
60
知识点三
当堂训练
关系定理的推论
3.如图,已知AB、CD为⊙O的两条弦,AD=BC,求证:AB=CD.
⌒
⌒
C
A
B
D
O
知识点三
当堂训练
关系定理的推论
证明:∵AD=BC
⌒
⌒
∴AD+BD=BC+BD
⌒
⌒
⌒
⌒
即AB=CD
⌒
⌒
∴AB=CD
圆心角
定理
推论
知识梳理
课堂小结
弧、弦、圆心角
顶点在圆心的角
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
要注意前提条件:在同圆或等圆中
弧、弦圆心角
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.3 弧、弦、圆心角
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
1.圆心角:
顶点在圆心的角叫做圆心角,如∠AOB .
O
A
B
4.圆心角∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
弦
3.圆心角的度数等于它所对的弧的度数.
知识点一
知识归纳
圆心角的定义
1.判断下列各图中的角是不是圆心角,并说明理由.
O
O
O
O
×
√
×
×
圆内角
圆心角
圆周角
圆外角
A
B
O
2.如图,在⊙O中,弦AB所对的劣弧为圆的1/3,圆的半径为4cm,求AB的长.
知识点一
当堂训练
圆心角的定义
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
【探究1】把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么 由此你能得到什么结论
【探究2】将圆绕圆心旋转180 后,得到的图形与原图形重合吗?由此你得到什么结论呢
O
所以圆是轴对称图形
O
A
B
180
所以圆是中心对称图形
知识点二
探究新知
弧、弦、圆心角之间的关系
【探究3】把圆绕圆心旋转任意一个角度呢 仍与原来的圆重合吗.
O
α
·
圆既是轴对称图形,
又是中心对称图形,
还具有旋转不变性。
由圆的轴对称性质得出---垂径定理。
由圆的旋转不变性可得出什么结论?
知识点二
探究新知
弧、弦、圆心角之间的关系
【在同圆中探究】在⊙O中,当圆心角∠AOB=∠A OB 时,它们所对的弧AB和弧A B ,弦AB和弦A B 相等吗?
O
A
B
A
B
AB=A B ,弧AB=弧A B
在同圆中∠AOB=∠A OB
知识点二
探究新知
弧、弦、圆心角之间的关系
条件:
结论:
【在等圆中探究】在等圆中,若∠AOB=∠A O B ,你发现的等量关系是否依然成立?
O
A
B
·
O
A
B
·
·
AB=A B ,弧AB=弧A B
在等圆中∠AOB=∠A OB
知识点二
探究新知
弧、弦、圆心角之间的关系
条件:
结论:
圆心角
相等
弧相等
弦相等
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角、弧、弦之间的关系定理:
思
考
举例说明:为什么要说“在同圆或等圆中”?
A
B
O
D
C
知识点二
知识归纳
弧、弦、圆心角之间的关系
小林根据在圆心角、弧、弦三个量之间的关系,认为在如图中,若∠AOB=2∠COD,则有AB=2CD,AB=2CD,你同意他的观点吗?试说明你的理由.
⌒
⌒
A
D
C
O
B
E
知识点二
当堂训练
弧、弦、圆心角之间的关系
圆心角的定义
01
弧,弦,圆心角之间的关系
02
关系定理的推论
03
知识要点
精讲精练
【探究1】在同圆或等圆中,如果两条弧相等,能得到什么结论?
【探究2】在同圆或等圆中,如果两条弦相等,能得到什么结论?
O
A
B
A
B
结论:∠AOB=∠A OB ,弧AB=弧A B
条件:在同圆或等圆中AB=A B
结论:AB=A B ,∠AOB=∠A OB ,
条件:在同圆或等圆中弧AB=弧A B
归纳:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
知识点三
探究新知
关系定理的推论
证明:
又∵∠ACB=60 ,
∴△ABC是等边三角形,AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
【例1】如图在⊙O中,AB=AC,∠ACB=60 ,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
∵AB=AC
⌒
⌒
·
B
C
O
A
∴AB=AC,△ABC等腰三角形.
知识点三
典例精讲
关系定理的推论
×
√
×
1.判断下列说法是否正确.
(1)相等的圆心角所对的弧相等. ( )
(2)等弧所对的弦相等. ( )
(3)相等的弦所对的弧相等. ( )
2.弦长等于半径的弦所对的圆心角等于 .
60
知识点三
当堂训练
关系定理的推论
3.如图,已知AB、CD为⊙O的两条弦,AD=BC,求证:AB=CD.
⌒
⌒
C
A
B
D
O
知识点三
当堂训练
关系定理的推论
证明:∵AD=BC
⌒
⌒
∴AD+BD=BC+BD
⌒
⌒
⌒
⌒
即AB=CD
⌒
⌒
∴AB=CD
圆心角
定理
推论
知识梳理
课堂小结
弧、弦、圆心角
顶点在圆心的角
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
要注意前提条件:在同圆或等圆中
弧、弦圆心角
同课章节目录
