2022-2023学年冀教版八年级数学上册 13.3《全等三角形的判定》解答专项练习题(含答案)
文档属性
| 名称 | 2022-2023学年冀教版八年级数学上册 13.3《全等三角形的判定》解答专项练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 348.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 19:13:51 | ||
图片预览

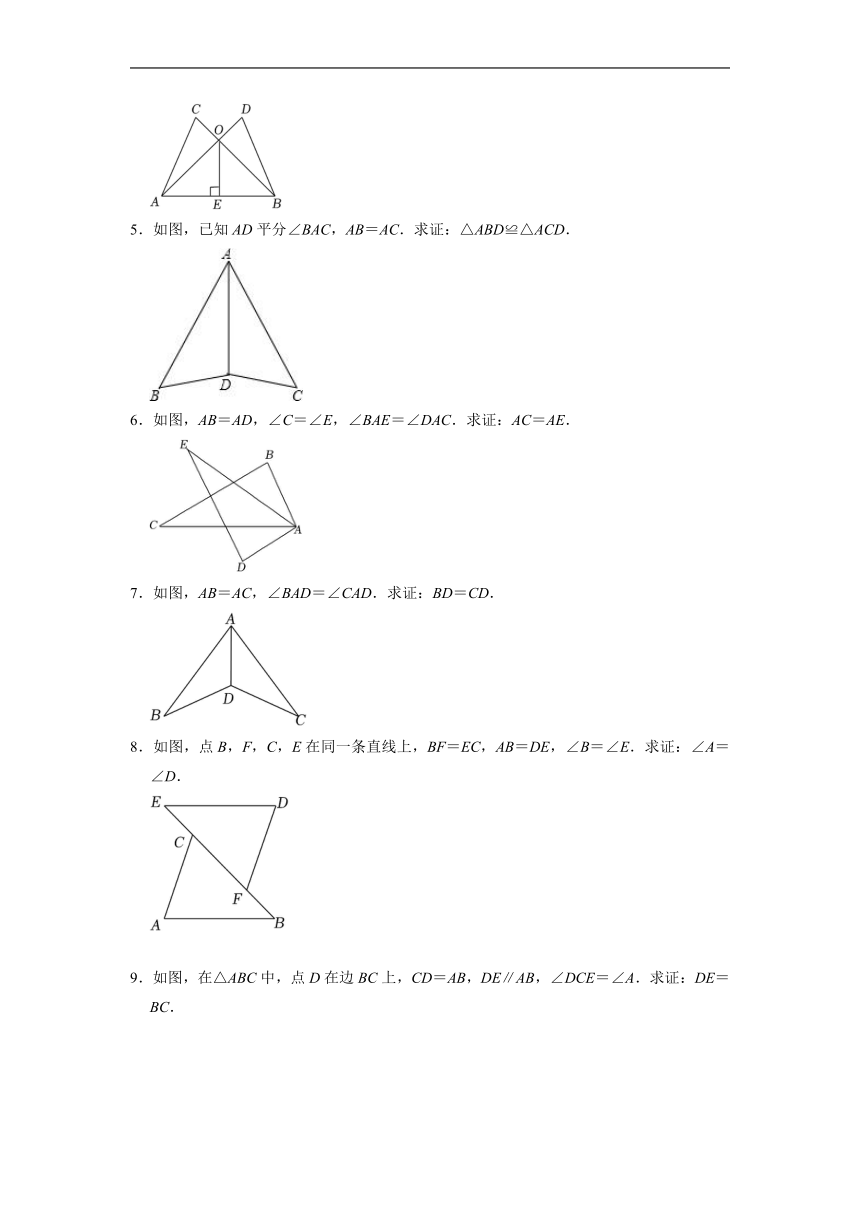

文档简介
2022-2023学年冀教版八年级数学上册《13.3全等三角形的判定》解答专项练习题(附答案)
1.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.
2.如图为某单摆装置示意图,摆线长OA=OB=OC,当摆线位于OB位置时,过点B作BD⊥OA于点D,测得OD=15cm,当摆线位于OC位置时,OB与OC恰好垂直,求此时摆球到OA的水平距离CE的长(CE⊥OA).
3.填空完成下列说理:
如图,AC与BD交于点O,联结AB、DC、BC,已知∠A=∠D,AO=DO.
说明:∠ABC=∠DCB.
在△AOB与△DOC中,
∠A=∠D(已知)
AO=DO(已知)
∠AOB=∠DOC( )
∴△AOB≌△DOC( )
∴∠ABO=∠DCO( )
OB=OC( )
∴∠OBC=∠OCB( )
∴∠OBC+∠ABO=∠OCB+∠DCO( )
即∠ABC=∠DCB.
已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.
求证: (1)△ABC≌△BAD.
(2)AE=BE.
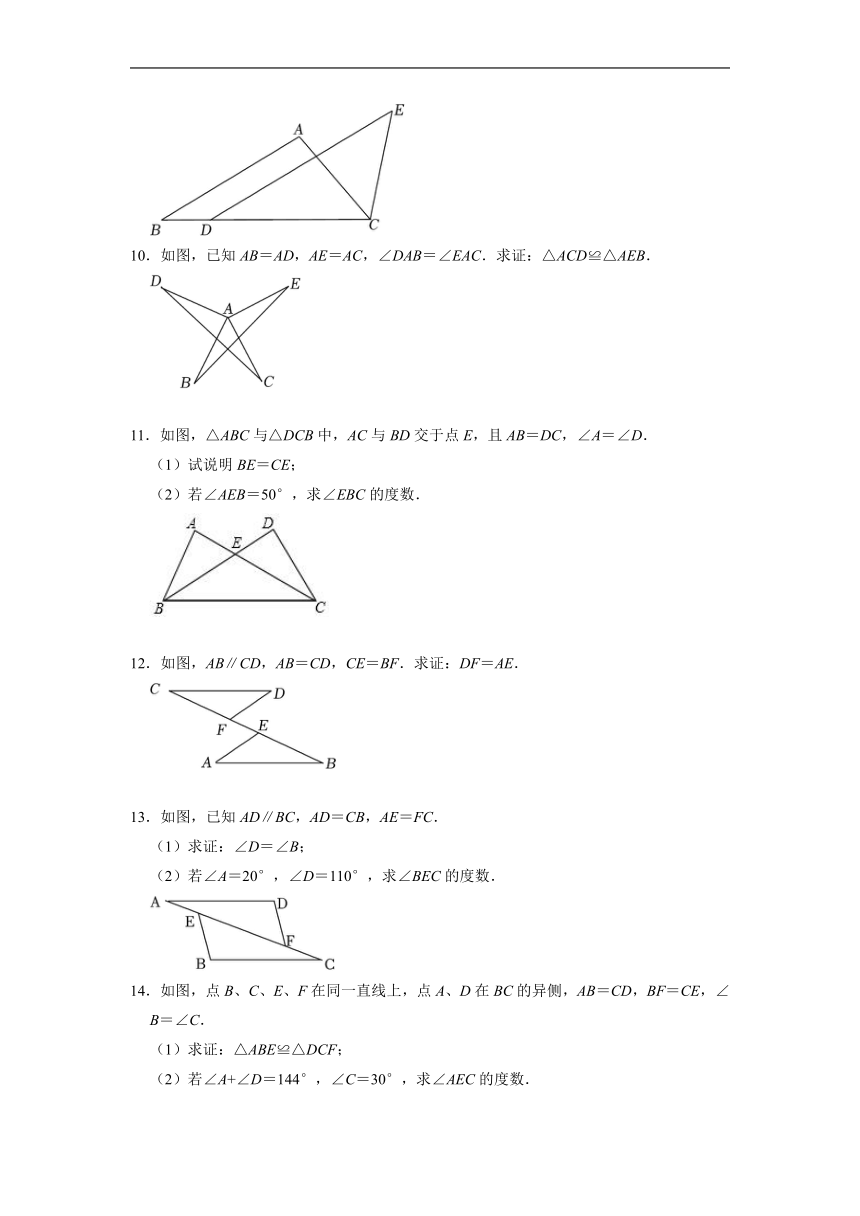
5.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
6.如图,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:AC=AE.
7.如图,AB=AC,∠BAD=∠CAD.求证:BD=CD.
8.如图,点B,F,C,E在同一条直线上,BF=EC,AB=DE,∠B=∠E.求证:∠A=∠D.
9.如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
10.如图,已知AB=AD,AE=AC,∠DAB=∠EAC.求证:△ACD≌△AEB.
11.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
12.如图,AB∥CD,AB=CD,CE=BF.求证:DF=AE.
13.如图,已知AD∥BC,AD=CB,AE=FC.
(1)求证:∠D=∠B;
(2)若∠A=20°,∠D=110°,求∠BEC的度数.
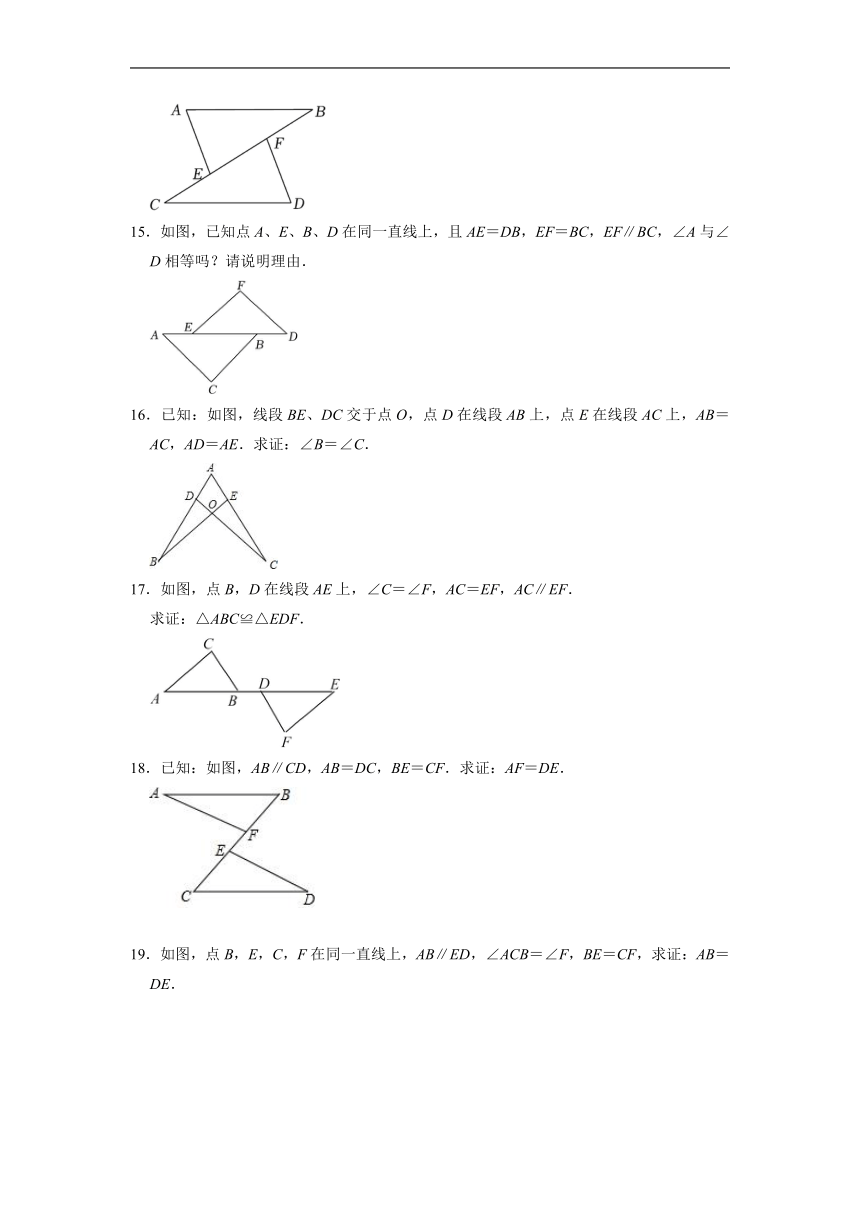
14.如图,点B、C、E、F在同一直线上,点A、D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:△ABE≌△DCF;
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
15.如图,已知点A、E、B、D在同一直线上,且AE=DB,EF=BC,EF∥BC,∠A与∠D相等吗?请说明理由.
16.已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
17.如图,点B,D在线段AE上,∠C=∠F,AC=EF,AC∥EF.
求证:△ABC≌△EDF.
18.已知:如图,AB∥CD,AB=DC,BE=CF.求证:AF=DE.
19.如图,点B,E,C,F在同一直线上,AB∥ED,∠ACB=∠F,BE=CF,求证:AB=DE.
20.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
21.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
22.如图,点B、E、C、F四点在一条直线上,AB=DE,AB∥DE.
老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AC=DF;
乙说:添加AC∥DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是 .
(2)请你从正确的说法中选择一种,给出你的证明.
参考答案
1.证明:∵∠3=∠4,
∴∠ACB=∠ACD,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(ASA),
∴AB=AD.
2.解:∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS),
∴CE=OD=15cm,
∴摆球到OA的水平距离CE的长为15cm.
3.解:在△AOB与△DOC中,
∠A=∠D(已知),
AO=DO(已知),
∠AOB=∠DOC(对顶角相等),
∴△AOB≌△DOC(ASA),
∴∠ABO=∠DCO(全等三角形的对应角相等),
OB=OC(全等三角形的对应边相等),
∴∠OBC=∠OCB(等边对等角),
∴∠OBC+∠ABO=∠OCB+∠DCO(等式性质),
即∠ABC=∠DCB.
4.证明(1)在ABC和△BAD中,
,
∴△ABC≌△BAD(SSS);
(2)∵△ABC≌△BAD,
∴∠CBA=∠DAB,
∴OA=OB,
∵OE⊥AB,
∴AE=BE.
5.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
6.证明:∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(AAS),
∴AC=AE.
7.证明:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD.
8.证明:∵BF=EC,
∴BF+CF=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
9.证明:∵DE∥AB,
∴∠EDC=∠B,
在△CDE和△ABC中,
,
∴△CDE≌△ABC(ASA),
∴DE=BC.
10.证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
在△ACD和△AEB中,
,
∴△ACD≌△AEB(SAS).
11.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴BE=CE;
(2)解:由(1)知,BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
12.证明:∵AB∥CD (已知),
∴∠C=∠B (两直线平行,内错角相等),
∵CE=BF,
∴CE﹣FE=BF﹣FE,
即CF=BE,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴DF=AE (全等三角形的对应边相等).
13.(1)证明:∵AD∥BC,
∴∠A=∠C,
∵AE=FC,
∴AF=CE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠D=∠B;
(2)解:∵∠A=20°,∠D=110°,
∴∠AFD=50°,
∵△ADF≌△CBE,
∴∠BEC=∠AFD=50°.
14.(1)证明:∵BF=CE,
∴BE=CF,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
(2)解:由(1)知,△ABE≌△DCF,
∴∠AEB=∠DFC,∠A=∠D,
∴∠AEC=∠DFB,
∵∠A+∠D=144°,
∴∠D=72°,
又∵∠C=30°,
∴∠DFB=∠C+∠D=102°,
∴∠AEC=102°.
15.解:相等,理由如下:
∵AE=DB,
∴AB=DE,
∵EF∥BC,
∴∠FED=∠CBA,
在△EFD与△BCA中,
,
∴△EFD≌△BCA(SAS),
∴∠A=∠D.
16.证明:在△ABE和△ACD中,
,
∴△ABE≌ACD(SAS),
∴∠B=∠C.
17.证明:∵AC∥EF,
∴∠A=∠E.
在△ABC和△EDF中,
,
∴△ABC≌△EDF(ASA).
18.证明:如图,∵AB∥CD,
∴∠B=∠C.
∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
在△ABF与△DCE中,
,
∴△ABF≌△DCE(SAS),
∴AF=DE.
19.证明:∵AB∥ED,
∴∠B=∠DEF,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE.
20.证明:∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴AC=BD.
21.证明:(1)∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ECA,
即∠BCA=∠DCE,
在△BCA和△DCE中,
,
∴△BCA≌△DCE(ASA),
∴BC=DC;
(2)∵△BCA≌△DCE,
∴∠B=∠D=15°,
∵∠A=25°,
∴∠ACB=180°﹣∠A﹣∠B=140°.
22.(1)解:说法正确的是:乙、丙,
故答案为:乙、丙;
(2)证明:∵AB∥DE,
∴∠B=∠DEC,
∵AC∥DF,
∴∠F=∠ACB,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
1.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.
2.如图为某单摆装置示意图,摆线长OA=OB=OC,当摆线位于OB位置时,过点B作BD⊥OA于点D,测得OD=15cm,当摆线位于OC位置时,OB与OC恰好垂直,求此时摆球到OA的水平距离CE的长(CE⊥OA).
3.填空完成下列说理:
如图,AC与BD交于点O,联结AB、DC、BC,已知∠A=∠D,AO=DO.
说明:∠ABC=∠DCB.
在△AOB与△DOC中,
∠A=∠D(已知)
AO=DO(已知)
∠AOB=∠DOC( )
∴△AOB≌△DOC( )
∴∠ABO=∠DCO( )
OB=OC( )
∴∠OBC=∠OCB( )
∴∠OBC+∠ABO=∠OCB+∠DCO( )
即∠ABC=∠DCB.
已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.
求证: (1)△ABC≌△BAD.
(2)AE=BE.
5.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
6.如图,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:AC=AE.
7.如图,AB=AC,∠BAD=∠CAD.求证:BD=CD.
8.如图,点B,F,C,E在同一条直线上,BF=EC,AB=DE,∠B=∠E.求证:∠A=∠D.
9.如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
10.如图,已知AB=AD,AE=AC,∠DAB=∠EAC.求证:△ACD≌△AEB.
11.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
12.如图,AB∥CD,AB=CD,CE=BF.求证:DF=AE.
13.如图,已知AD∥BC,AD=CB,AE=FC.
(1)求证:∠D=∠B;
(2)若∠A=20°,∠D=110°,求∠BEC的度数.
14.如图,点B、C、E、F在同一直线上,点A、D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:△ABE≌△DCF;
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
15.如图,已知点A、E、B、D在同一直线上,且AE=DB,EF=BC,EF∥BC,∠A与∠D相等吗?请说明理由.
16.已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
17.如图,点B,D在线段AE上,∠C=∠F,AC=EF,AC∥EF.
求证:△ABC≌△EDF.
18.已知:如图,AB∥CD,AB=DC,BE=CF.求证:AF=DE.
19.如图,点B,E,C,F在同一直线上,AB∥ED,∠ACB=∠F,BE=CF,求证:AB=DE.
20.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
21.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
22.如图,点B、E、C、F四点在一条直线上,AB=DE,AB∥DE.
老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AC=DF;
乙说:添加AC∥DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是 .
(2)请你从正确的说法中选择一种,给出你的证明.
参考答案
1.证明:∵∠3=∠4,
∴∠ACB=∠ACD,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(ASA),
∴AB=AD.
2.解:∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS),
∴CE=OD=15cm,
∴摆球到OA的水平距离CE的长为15cm.
3.解:在△AOB与△DOC中,
∠A=∠D(已知),
AO=DO(已知),
∠AOB=∠DOC(对顶角相等),
∴△AOB≌△DOC(ASA),
∴∠ABO=∠DCO(全等三角形的对应角相等),
OB=OC(全等三角形的对应边相等),
∴∠OBC=∠OCB(等边对等角),
∴∠OBC+∠ABO=∠OCB+∠DCO(等式性质),
即∠ABC=∠DCB.
4.证明(1)在ABC和△BAD中,
,
∴△ABC≌△BAD(SSS);
(2)∵△ABC≌△BAD,
∴∠CBA=∠DAB,
∴OA=OB,
∵OE⊥AB,
∴AE=BE.
5.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
6.证明:∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(AAS),
∴AC=AE.
7.证明:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD.
8.证明:∵BF=EC,
∴BF+CF=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
9.证明:∵DE∥AB,
∴∠EDC=∠B,
在△CDE和△ABC中,
,
∴△CDE≌△ABC(ASA),
∴DE=BC.
10.证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
在△ACD和△AEB中,
,
∴△ACD≌△AEB(SAS).
11.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴BE=CE;
(2)解:由(1)知,BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
12.证明:∵AB∥CD (已知),
∴∠C=∠B (两直线平行,内错角相等),
∵CE=BF,
∴CE﹣FE=BF﹣FE,
即CF=BE,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴DF=AE (全等三角形的对应边相等).
13.(1)证明:∵AD∥BC,
∴∠A=∠C,
∵AE=FC,
∴AF=CE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠D=∠B;
(2)解:∵∠A=20°,∠D=110°,
∴∠AFD=50°,
∵△ADF≌△CBE,
∴∠BEC=∠AFD=50°.
14.(1)证明:∵BF=CE,
∴BE=CF,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
(2)解:由(1)知,△ABE≌△DCF,
∴∠AEB=∠DFC,∠A=∠D,
∴∠AEC=∠DFB,
∵∠A+∠D=144°,
∴∠D=72°,
又∵∠C=30°,
∴∠DFB=∠C+∠D=102°,
∴∠AEC=102°.
15.解:相等,理由如下:
∵AE=DB,
∴AB=DE,
∵EF∥BC,
∴∠FED=∠CBA,
在△EFD与△BCA中,
,
∴△EFD≌△BCA(SAS),
∴∠A=∠D.
16.证明:在△ABE和△ACD中,
,
∴△ABE≌ACD(SAS),
∴∠B=∠C.
17.证明:∵AC∥EF,
∴∠A=∠E.
在△ABC和△EDF中,
,
∴△ABC≌△EDF(ASA).
18.证明:如图,∵AB∥CD,
∴∠B=∠C.
∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
在△ABF与△DCE中,
,
∴△ABF≌△DCE(SAS),
∴AF=DE.
19.证明:∵AB∥ED,
∴∠B=∠DEF,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE.
20.证明:∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴AC=BD.
21.证明:(1)∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ECA,
即∠BCA=∠DCE,
在△BCA和△DCE中,
,
∴△BCA≌△DCE(ASA),
∴BC=DC;
(2)∵△BCA≌△DCE,
∴∠B=∠D=15°,
∵∠A=25°,
∴∠ACB=180°﹣∠A﹣∠B=140°.
22.(1)解:说法正确的是:乙、丙,
故答案为:乙、丙;
(2)证明:∵AB∥DE,
∴∠B=∠DEC,
∵AC∥DF,
∴∠F=∠ACB,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
