2022-2023学年苏科版九年级数学上册 2.2 圆的对称性 同步练习题 (含解析)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学上册 2.2 圆的对称性 同步练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 552.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 20:10:44 | ||
图片预览




文档简介
2022-2023学年苏科版九年级数学上册《2.2圆的对称性》同步练习题(附答案)
一.选择题
1.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm
2.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2 B.2 C.2 D.4
3.如图,坐标平面上,A、B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
A.﹣2 B.﹣2 C.﹣8 D.﹣7
4.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
5.如图,点A、B是在⊙O上的定点、P是在⊙O上的动点,要使△ABP为等腰三角形,则所有符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
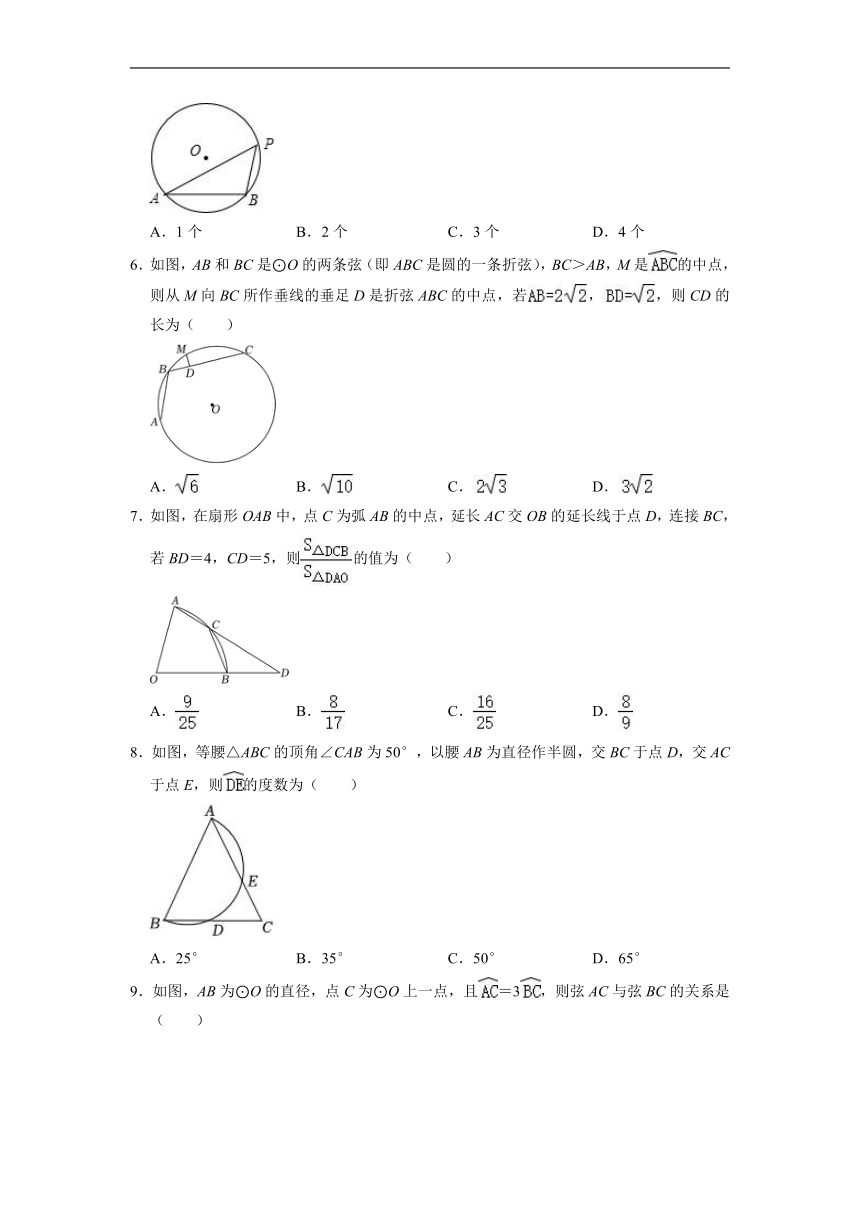
6.如图,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,若,,则CD的长为( )
A. B. C. D.
7.如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=5,则的值为( )
A. B. C. D.
8.如图,等腰△ABC的顶角∠CAB为50°,以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( )
A.25° B.35° C.50° D.65°
9.如图,AB为⊙O的直径,点C为⊙O上一点,且=3,则弦AC与弦BC的关系是( )
A.AC=3BC B.AC=BC C.AC=(+1)BC D.AC=BC
10.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
11.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与点M,N重合,数学学习小组在探究时得出以下结论:
①PB+PA是定值;
②当点P是的中点时,四边形PAOB是正方形;
③当点P在上移动时,矩形PAOB的大小随之变化,但AB的长度不变;
④连接MP,PN,若=2,则MP=2PN.
以上结论正确的序号是( )
A.①②④ B.②③④ C.②③ D.①②③④
二.填空题
12.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
13.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
14.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
15.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
16.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
17.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 .
18.如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2﹣EF2,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为 .
三.解答题
19.如图,在半径为2的扇形OAB中,∠AOB=90°,点C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.
(1)当BC=2时,求线段OD的长和∠BOD的度数;
(2)在△DOE中,是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
(3)在△DOE中,是否存在度数保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.
20.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
21.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,求⊙O的半径及EC的长.
22.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
23.如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.
参考答案
一.选择题
1.解:如图所示,CD⊥AB于点P.
根据题意,得:AB=10cm,CD=6cm.
∵AB是直径,且CD⊥AB,
∴CP=CD=3cm.
根据勾股定理,得OP===4(cm).
故选:B.
2.解:过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,如图所示:
则DF=CF,AG=BG=AB=3,
∴EG=AG﹣AE=2,
在Rt△BOG中,OG===2,
∴EG=OG,
∴△EOG是等腰直角三角形,
∴∠OEG=45°,OE=OG=2,
∵∠DEB=75°,
∴∠OEF=30°,
∴OF=OE=,
在Rt△ODF中,DF===,
∴CD=2DF=2;
故选:C.
3.解:连接AC,
由题意得,BC=OB+OC=9,
∵直线L通过P点且与AB垂直,
∴直线L是线段AB的垂直平分线,
∴AC=BC=9,
在Rt△AOC中,AO==2,
∵a<0,
∴a=﹣2,
故选:A.
4.解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连接PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE=,
∴PD=PE=,
∴a=3+.
故选:B.
5.解:如图:①以AB为底边,
过点O作弦AB的垂线分别交⊙O于点P1、P2,
∴AP1=BP1,AP2=BP2,
故点P1、P2即为所求.
②以AB为腰,
分别以点A、点B为圆心,以AB长为半径画弧,交⊙O于点P3、P4,
故点P3、P4即为所求.
共4个点.
故选:D.
6.解:如图,在CD上截取CE=AB,连接CM,EM,BM,AM,
∵M是的中点,
∴AM=CM,
又∠A=∠C,
在△ABM和△CEM中,
,
∴△ABM≌△CEM(SAS),
∴BM=EM,
∵MD⊥BC,
∴BD=DE,
∵,,
∴CD=CE+DE=AB+BD=2=3.
故选:D.
7.解:连接OC,
∵点C为弧AB的中点,
∴∠AOC=∠BOC,OA=OC=OB,
∴△AOC≌△BOC,
∴∠A=∠OBC=∠OCA=∠OCB,
又∠DBC=∠DCO,
∵BD=4,CD=5,
∴,
解得:DO=,
∴OB=OD﹣BD=,
∴,
∴,
∴.
故选:B.
8.解:设圆心为O,连接OE、OD,
∵AB=AC,
∴∠ABC=∠ACB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠ACB,
∴OD∥AC,
∴∠DOE=∠OEA,
∵OA=OE,
∴∠BAC=∠OEA,
∴∠DOE=∠BAC=50°,
即弧DE的度数为50°,
故选:C.
9.解:如图,过点O作OD⊥AB,交AC于D,连接BD,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=3,
∴∠AOC=135°,
∵OA=OC,
∴∠A=∠ACO=22.5°,
∵OD是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=22.5°,
∴∠CDB=∠CBD=45°,
设CD=CB=x,则AD=BD=x,
∴==,
∴AC=(+1)BC.
故选:C.
10.解:如图,过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∴∠APO=∠AQO=90°,
∵∠A=50°,
∴∠POQ=360°﹣90°﹣90°﹣50°=130°,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
∴∠BOC==115°.
故选:C.
11.解:设半径为r,连接OP,
∵四边形PAOB为矩形,
∴PB=AO,∠OAP=∠AOB=∠OBP=90°,
当∠OPA=30°时,在Rt△OAP中,OA==,PA=,此时PA+PB=;
当∠OPA=45°时,在Rt△OAP中,OA=PA=,此时PA+PB=;
∴PB+PA不是定值,故①不正确;
∵点P是的中点,
∴,
∴∠AOP=∠BOP=45°,
∴∠OPA=180°﹣90°﹣45°=45°,
∴∠AOP=∠OPA,
∴AP=AO,
∴矩形PAOB是正方形,故②正确;
点P在上移动时,半径一定,且AB=OP=r,
∴当点P在上移动时,矩形PAOB的大小随之变化,但AB的长度不变,故③正确;
∵=2,
∴∠MOP=2∠PON,
∴∠MOP==60°,∠PON=∠AOB=30°,
∵OB=OM,
∴△OPM是等边三角形,
∴MP=OP=r,
在Rt△OBP中,∠PON=30°,
∴PB=<PN,
∴2PN>r,
∴2PN>MP,故④不正确.
故选:C.
二.填空题
12.解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×1=,
即CD的最大值为,
故答案为:.
13.解:作半径OD⊥AB于C,连接OB,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
14.解:∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵MF⊥CD,CD∥OB,
∴MF⊥OB,
∴∠CFM=∠EMF=90°,
又∵∠OEM=90°,
∴四边形CEMF是矩形,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
15.解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,
CD=DB=DA==,
所以D是过A,B,C三点的圆的圆心,
即D的坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2),
16.解:连接OB,OC,作CH垂直AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
17.解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,
∴OD=OA=3,
在Rt△OPD中,
∵OP=,OD=3,
∴PD===2,
∴P(3,2).
故答案为:(3,2).
18.解:延长CO交AB于G,
∵点C是⊙O优弧ACB上的中点,
∴CO⊥AB,AG=AB=×6=3(cm),
∴AE2=AG2+EG2,EF2=FG2+EG2,
当0≤x≤3时,AF=xcm,FG=(3﹣x)cm,
∴y=AE2﹣EF2=AG2+EG2﹣FG2﹣EG2=AG2﹣FG2=9﹣(3﹣x)2=6x﹣x2;
当3<x≤6时,AF=xcm,FG=(x﹣3)cm,
∴y=AE2﹣EF2=AG2+EG2﹣FG2﹣EG2=AG2﹣FG2=9﹣(x﹣3)2=6x﹣x2.
故答案为:y=6x﹣x2.
三.解答题
19.解:(1)如图,
∵OD⊥BC,
∴BD=CD=,
∴,
∴∠BOD=30°;
由勾股定理得:
OD2=22﹣12=3,
∴OD=;
即线段OD的长和∠BOD的度数分别为、30°.
(2)存在,DE=;
如图,连接AB;
∵∠AOB=90°,OA=OB=2,
∴AB2=OB2+OA2=8,
∴AB=;
∵OD⊥BC,OE⊥AC,
∴BD=CD,AE=EC,
∴DE是△ABC的中位线,
DE==.
(3)存在,∠DOE=45°;
∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠BOD=∠COD,∠AOE=∠COE,
∴∠DOE=,
即∠DOE=45°.
20.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
21.解:∵OD⊥弦AB,AB=8,
∴AC===4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
22.解:(1)如图,设圆心为O,连接OB,OC.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)连接ON.∵CD=4m,船舱顶部为长方形并高出水面AB=3.6m,
∴CE=4﹣3.6=0.4(m),
∴OE=r﹣CE=6.5﹣0.4=6.1(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣6.12=5.042,
∴EN=(m).
∴MN=2EN=2×≈4.48m<5m.
∴此货船不能顺利通过这座拱桥.
23.解:(1)∵在三角形ABC中,∠ACB=90°,AC=3,BC=4,
∴AB===5,
点C作CE⊥AB于点E,则AD=2AE,
∵∠CAE=∠CAB,∠AEC=∠ACB=90°,
∴AC2=AE AB,即32=AE×5
∴AE=1.8,
∴AD=2AE=2×1.8=3.6
∴BD=AB﹣AD=5﹣3.6=1.4.
一.选择题
1.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm
2.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2 B.2 C.2 D.4
3.如图,坐标平面上,A、B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
A.﹣2 B.﹣2 C.﹣8 D.﹣7
4.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
5.如图,点A、B是在⊙O上的定点、P是在⊙O上的动点,要使△ABP为等腰三角形,则所有符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
6.如图,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,若,,则CD的长为( )
A. B. C. D.
7.如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=5,则的值为( )
A. B. C. D.
8.如图,等腰△ABC的顶角∠CAB为50°,以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( )
A.25° B.35° C.50° D.65°
9.如图,AB为⊙O的直径,点C为⊙O上一点,且=3,则弦AC与弦BC的关系是( )
A.AC=3BC B.AC=BC C.AC=(+1)BC D.AC=BC
10.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
11.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与点M,N重合,数学学习小组在探究时得出以下结论:
①PB+PA是定值;
②当点P是的中点时,四边形PAOB是正方形;
③当点P在上移动时,矩形PAOB的大小随之变化,但AB的长度不变;
④连接MP,PN,若=2,则MP=2PN.
以上结论正确的序号是( )
A.①②④ B.②③④ C.②③ D.①②③④
二.填空题
12.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
13.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
14.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
15.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
16.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
17.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 .
18.如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2﹣EF2,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为 .
三.解答题
19.如图,在半径为2的扇形OAB中,∠AOB=90°,点C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.
(1)当BC=2时,求线段OD的长和∠BOD的度数;
(2)在△DOE中,是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
(3)在△DOE中,是否存在度数保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.
20.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
21.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,求⊙O的半径及EC的长.
22.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
23.如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.
参考答案
一.选择题
1.解:如图所示,CD⊥AB于点P.
根据题意,得:AB=10cm,CD=6cm.
∵AB是直径,且CD⊥AB,
∴CP=CD=3cm.
根据勾股定理,得OP===4(cm).
故选:B.
2.解:过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,如图所示:
则DF=CF,AG=BG=AB=3,
∴EG=AG﹣AE=2,
在Rt△BOG中,OG===2,
∴EG=OG,
∴△EOG是等腰直角三角形,
∴∠OEG=45°,OE=OG=2,
∵∠DEB=75°,
∴∠OEF=30°,
∴OF=OE=,
在Rt△ODF中,DF===,
∴CD=2DF=2;
故选:C.
3.解:连接AC,
由题意得,BC=OB+OC=9,
∵直线L通过P点且与AB垂直,
∴直线L是线段AB的垂直平分线,
∴AC=BC=9,
在Rt△AOC中,AO==2,
∵a<0,
∴a=﹣2,
故选:A.
4.解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连接PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE=,
∴PD=PE=,
∴a=3+.
故选:B.
5.解:如图:①以AB为底边,
过点O作弦AB的垂线分别交⊙O于点P1、P2,
∴AP1=BP1,AP2=BP2,
故点P1、P2即为所求.
②以AB为腰,
分别以点A、点B为圆心,以AB长为半径画弧,交⊙O于点P3、P4,
故点P3、P4即为所求.
共4个点.
故选:D.
6.解:如图,在CD上截取CE=AB,连接CM,EM,BM,AM,
∵M是的中点,
∴AM=CM,
又∠A=∠C,
在△ABM和△CEM中,
,
∴△ABM≌△CEM(SAS),
∴BM=EM,
∵MD⊥BC,
∴BD=DE,
∵,,
∴CD=CE+DE=AB+BD=2=3.
故选:D.
7.解:连接OC,
∵点C为弧AB的中点,
∴∠AOC=∠BOC,OA=OC=OB,
∴△AOC≌△BOC,
∴∠A=∠OBC=∠OCA=∠OCB,
又∠DBC=∠DCO,
∵BD=4,CD=5,
∴,
解得:DO=,
∴OB=OD﹣BD=,
∴,
∴,
∴.
故选:B.
8.解:设圆心为O,连接OE、OD,
∵AB=AC,
∴∠ABC=∠ACB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠ACB,
∴OD∥AC,
∴∠DOE=∠OEA,
∵OA=OE,
∴∠BAC=∠OEA,
∴∠DOE=∠BAC=50°,
即弧DE的度数为50°,
故选:C.
9.解:如图,过点O作OD⊥AB,交AC于D,连接BD,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=3,
∴∠AOC=135°,
∵OA=OC,
∴∠A=∠ACO=22.5°,
∵OD是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=22.5°,
∴∠CDB=∠CBD=45°,
设CD=CB=x,则AD=BD=x,
∴==,
∴AC=(+1)BC.
故选:C.
10.解:如图,过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∴∠APO=∠AQO=90°,
∵∠A=50°,
∴∠POQ=360°﹣90°﹣90°﹣50°=130°,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
∴∠BOC==115°.
故选:C.
11.解:设半径为r,连接OP,
∵四边形PAOB为矩形,
∴PB=AO,∠OAP=∠AOB=∠OBP=90°,
当∠OPA=30°时,在Rt△OAP中,OA==,PA=,此时PA+PB=;
当∠OPA=45°时,在Rt△OAP中,OA=PA=,此时PA+PB=;
∴PB+PA不是定值,故①不正确;
∵点P是的中点,
∴,
∴∠AOP=∠BOP=45°,
∴∠OPA=180°﹣90°﹣45°=45°,
∴∠AOP=∠OPA,
∴AP=AO,
∴矩形PAOB是正方形,故②正确;
点P在上移动时,半径一定,且AB=OP=r,
∴当点P在上移动时,矩形PAOB的大小随之变化,但AB的长度不变,故③正确;
∵=2,
∴∠MOP=2∠PON,
∴∠MOP==60°,∠PON=∠AOB=30°,
∵OB=OM,
∴△OPM是等边三角形,
∴MP=OP=r,
在Rt△OBP中,∠PON=30°,
∴PB=<PN,
∴2PN>r,
∴2PN>MP,故④不正确.
故选:C.
二.填空题
12.解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×1=,
即CD的最大值为,
故答案为:.
13.解:作半径OD⊥AB于C,连接OB,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
14.解:∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵MF⊥CD,CD∥OB,
∴MF⊥OB,
∴∠CFM=∠EMF=90°,
又∵∠OEM=90°,
∴四边形CEMF是矩形,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
15.解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,
CD=DB=DA==,
所以D是过A,B,C三点的圆的圆心,
即D的坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2),
16.解:连接OB,OC,作CH垂直AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
17.解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,
∴OD=OA=3,
在Rt△OPD中,
∵OP=,OD=3,
∴PD===2,
∴P(3,2).
故答案为:(3,2).
18.解:延长CO交AB于G,
∵点C是⊙O优弧ACB上的中点,
∴CO⊥AB,AG=AB=×6=3(cm),
∴AE2=AG2+EG2,EF2=FG2+EG2,
当0≤x≤3时,AF=xcm,FG=(3﹣x)cm,
∴y=AE2﹣EF2=AG2+EG2﹣FG2﹣EG2=AG2﹣FG2=9﹣(3﹣x)2=6x﹣x2;
当3<x≤6时,AF=xcm,FG=(x﹣3)cm,
∴y=AE2﹣EF2=AG2+EG2﹣FG2﹣EG2=AG2﹣FG2=9﹣(x﹣3)2=6x﹣x2.
故答案为:y=6x﹣x2.
三.解答题
19.解:(1)如图,
∵OD⊥BC,
∴BD=CD=,
∴,
∴∠BOD=30°;
由勾股定理得:
OD2=22﹣12=3,
∴OD=;
即线段OD的长和∠BOD的度数分别为、30°.
(2)存在,DE=;
如图,连接AB;
∵∠AOB=90°,OA=OB=2,
∴AB2=OB2+OA2=8,
∴AB=;
∵OD⊥BC,OE⊥AC,
∴BD=CD,AE=EC,
∴DE是△ABC的中位线,
DE==.
(3)存在,∠DOE=45°;
∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠BOD=∠COD,∠AOE=∠COE,
∴∠DOE=,
即∠DOE=45°.
20.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
21.解:∵OD⊥弦AB,AB=8,
∴AC===4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
22.解:(1)如图,设圆心为O,连接OB,OC.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)连接ON.∵CD=4m,船舱顶部为长方形并高出水面AB=3.6m,
∴CE=4﹣3.6=0.4(m),
∴OE=r﹣CE=6.5﹣0.4=6.1(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣6.12=5.042,
∴EN=(m).
∴MN=2EN=2×≈4.48m<5m.
∴此货船不能顺利通过这座拱桥.
23.解:(1)∵在三角形ABC中,∠ACB=90°,AC=3,BC=4,
∴AB===5,
点C作CE⊥AB于点E,则AD=2AE,
∵∠CAE=∠CAB,∠AEC=∠ACB=90°,
∴AC2=AE AB,即32=AE×5
∴AE=1.8,
∴AD=2AE=2×1.8=3.6
∴BD=AB﹣AD=5﹣3.6=1.4.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
