2022—2023学年华东师大版八年级数学下册18.2平行四边形的判定 同步练习题(含答案)
文档属性
| 名称 | 2022—2023学年华东师大版八年级数学下册18.2平行四边形的判定 同步练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 22:51:44 | ||
图片预览



文档简介
2022-2023学年华师大版八年级数学下册《18-2平行四边形的判定》同步练习题(附答案)
一.选择题
1.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC C.∠A=∠C D.∠B+∠C=180°
2.下列条件中,能判定一个四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等 B.一组对边平行,一组对角相等
C.一组邻边相等,一组对角相等 D.一组对边平行,一组对角互补
3.如图,在四边形ABCD中,对角线AC,BD相交于点O,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC B.AB=CD.AD=BC
C.AD∥BC,∠ABC=∠ADC D.AB=CD,∠ABC=∠ADC
4.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
5.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
6.在等腰△ABC中,AB=AC=5,BC=6,D、E分别为AB、BC边上的中点,连接DE并延长DE到F,使得EF=2ED,连接AE、CF,则CF长为( )
A.4 B.2 C.5 D.3
7.如图,四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
8.如图,在 ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH.有下列结论:①GF⊥BD;②GF=EH;③四边形EGFH是平行四边形;④EG=FH.则正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行
B.一组对边平行,另一组对边相等
C.两条对角线互相平分
D.两组对边分别相等
二.填空题
10.已知O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .
11.在四边形ABCD中,若AB∥CD,BC AD,则四边形ABCD为平行四边形.
12.已知:如图,四边形ABCD中,AB∥CD,AB=CD,AC与BD相交于点O,则图中全等的三角形共有 对.
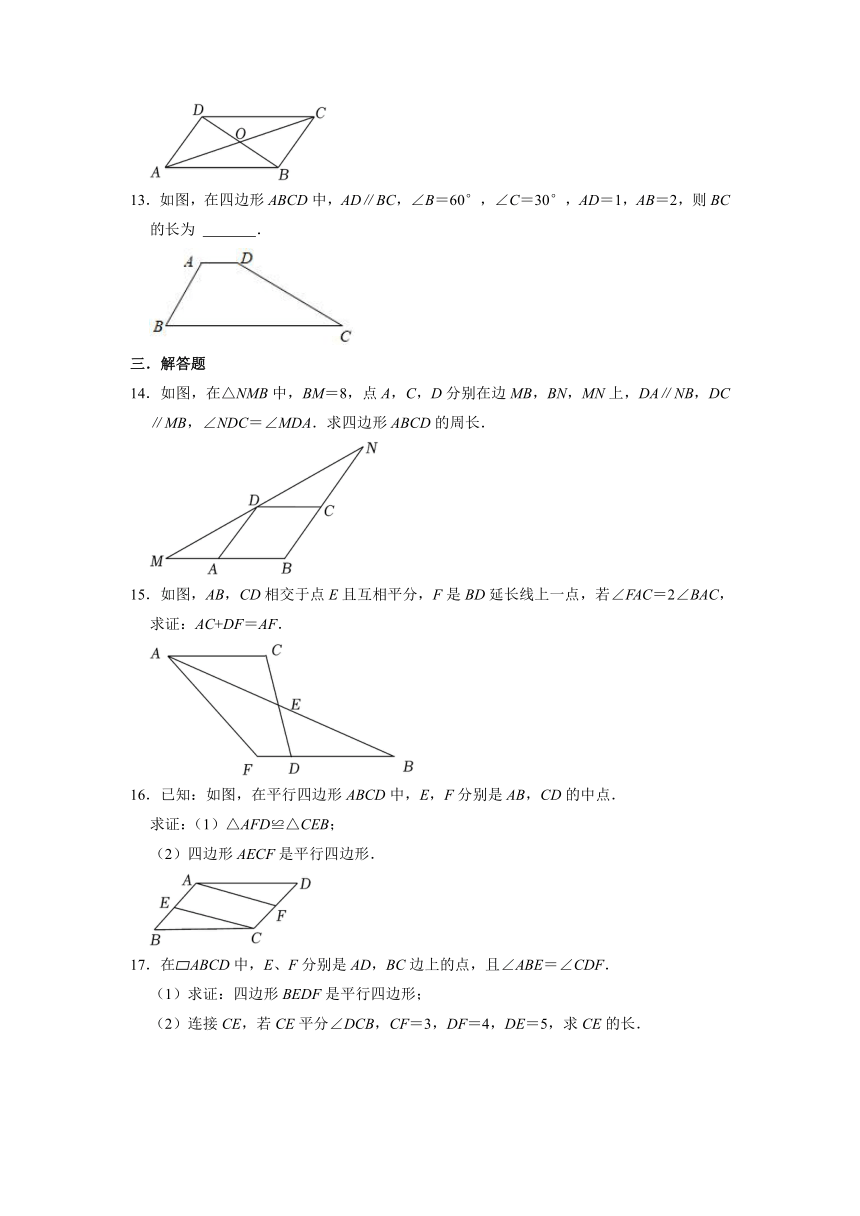
13.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
三.解答题
14.如图,在△NMB中,BM=8,点A,C,D分别在边MB,BN,MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.
15.如图,AB,CD相交于点E且互相平分,F是BD延长线上一点,若∠FAC=2∠BAC,求证:AC+DF=AF.
16.已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
17.在 ABCD中,E、F分别是AD,BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DF=4,DE=5,求CE的长.
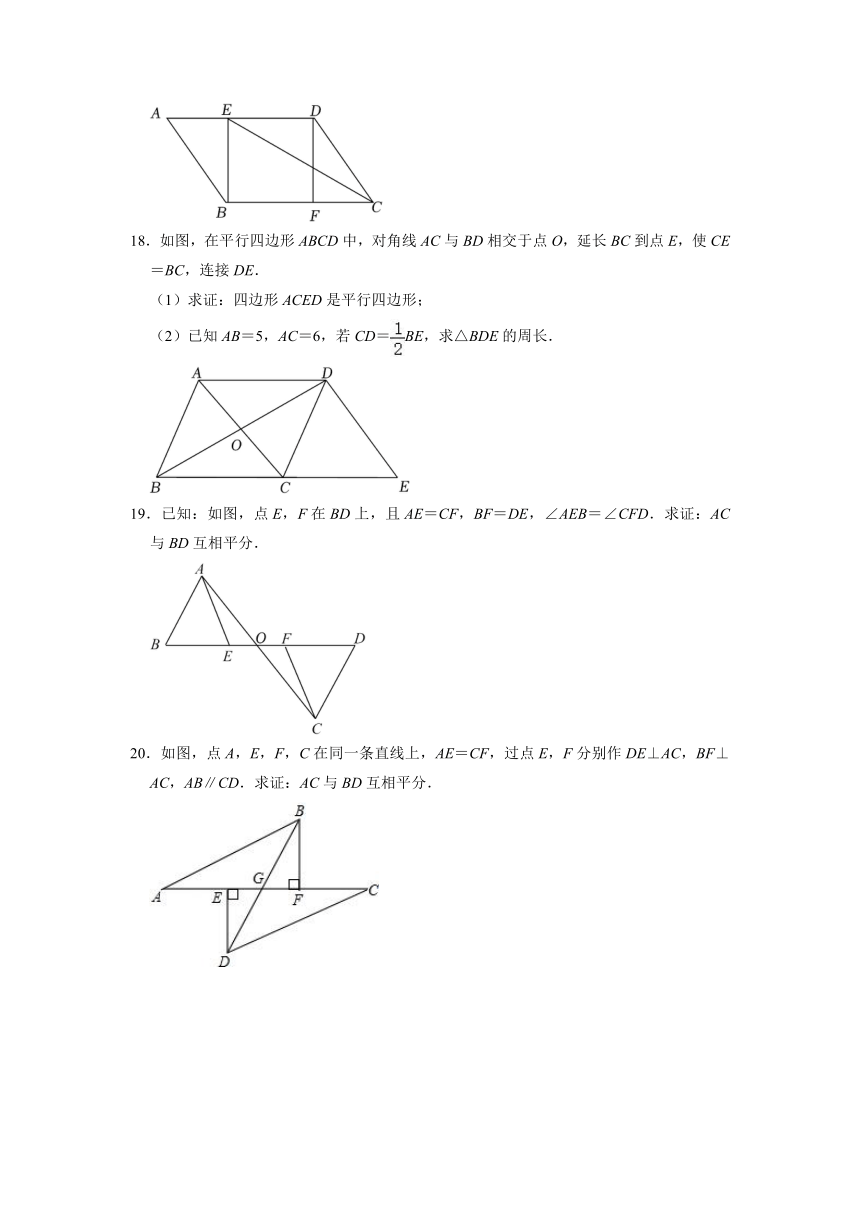
18.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,延长BC到点E,使CE=BC,连接DE.
(1)求证:四边形ACED是平行四边形;
(2)已知AB=5,AC=6,若CD=BE,求△BDE的周长.
19.已知:如图,点E,F在BD上,且AE=CF,BF=DE,∠AEB=∠CFD.求证:AC与BD互相平分.
20.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
参考答案
一.选择题
1.解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
2.解:A、一组对边平行,另一组对边相等,可能是等腰梯形,不一定是平行四边形,故选项A不符合题意;
B、一组对边平行,一组对角相等,可得到两组对边分别平行,为平行四边形,故选项B符合题意;
C、由一组邻边相等,一组对角相等,不能判定一个四边形是平行四边形,故选项C不符合题意;
D、一组对边平行,一组对角互补,可能是等腰梯形,不一定是平行四边形,故选项D不符合题意;
故选:B.
3.解:A、∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=CD.AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BAD=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
D、由AB=CD,∠ABC=∠ADC,不能判定四边形ABCD是平行四边形,故选项D符合题意;
故选:D.
4.解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
5.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
6.解:∵AB=AC=5,BC=6,E为BC边上的中点,
∴AE⊥BC,BE=EC=3,
在Rt△AEC中,AE===4,
∵D、E分别为AB、BC边上的中点,
∴DE∥AC,DE=AC,
∵EF=2ED,
∴EF=AC,
∴四边形EACF为平行四边形,
∴CF=AE=4,
故选:A.
7.解:线段EF与AC交于点O且互相平分,得OA=OC,OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴∠EAO=∠FCO,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴CD=AB,
∴四边形CDEF的周长=CD+DE+EF+CF=CD+AB+DE+AE=CD+AB+AD=6+6+10=22;
故选:C.
8.解:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠GBF=∠HDE,
在△GBF和△HDE中,
,
∴△GBF≌△HDE(SAS),
∴GF=EH,∠BGF=∠DHE,
∴∠FGH=∠EHG,
∴GF∥EH,
∴四边形EGFH是平行四边形,
∴EG=FH,故②③④正确,
∵∠FGH不一定等于90°,
∴GF⊥BD不正确,
故选:C.
9.解:A、一组对边相等且平行的四边形是平行四边形,故本选项不符合题意;
B、一组对边平行且另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形,故本选项符合题意;
C、两条对角线互相平分是平行四边形,故本选项不符合题意;
D、两组对边分别相等的四边形是平行四边形,故本选项不符合题意;
故选:B.
二.填空题
10.解:分三种情况:
①当四边形OABM为平行四边形时,如图1所示:
则BM∥AO,BM=AO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点O向左平移3﹣(﹣1)=4(个)单位,再向上平移1个单位得M的坐标,
∴M(﹣4,1);
②当四边形OAMB为平行四边形时,如图2所示:
则BM∥AO,BM=AO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点B向右平移3个单位,再向上平移1个单位得M的坐标,
∴M(2,3);
③当四边形OBAMM为平行四边形时,如图3所示:
则AB∥MO,AB=MO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点A向右平移1个单位,再向下平移2个单位得M的坐标,
∴M(4,﹣1);
综上所述,点M的坐标为(﹣4,1)或(2,3)或(4,﹣1);
故答案为:(﹣4,1)或(2,3)或(4,﹣1).
11.解:根据两组对边分别平行的四边形是平行四边形可知:
∵AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
故答案为:∥.
12.解:∵AB∥CD,AB=CD,
∴四边形ABCD为平行四边形,
∴OA=OC,OB=OD,AD=BC,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
同理可得△ACD≌△CAB(SSS);
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
同理可得△AOD≌△COB(SAS);
∴全等三角形有4对,
故答案为:4.
13.解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE=2,AD=BE=1,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°﹣60°﹣30°=90°.
∴EC=2DE=4.
∴BC=BE+EC=1+4=5.
故答案是:5.
三.解答题
14.解:∵DA∥NB,DC∥MB,
∴∠NDC=∠M,四边形ABCD为平行四边形,
∴DC=AB,AD=BC,
∵∠NDC=∠MDA.
∴AD=AM,
∴四边形ABCD的周长=AB+BC+CD+AD=2AM+2AB=2BM=2×8=16.
15.证明:连接AD、BC,
∵AB,CD相交于点E且互相平分,
∴四边形ACBD是平行四边形,
∴AC=BC,AC∥BC,
∴∠BAC=∠ABF,
∵∠FAC=2∠BAC,
∴∠FAB=∠BAC,
∴∠ABF=∠FAB,
∴AF=BF,
∵AC+DF=BD+DF=BF,
∴AC+DF=AF.
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠DCF,AB=CD,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴DE=BF,
∵DE∥BF,
∴四边形BFDE是平行四边形;
(2)∵四边形BFDE是平行四边形,
∴BE=DF,BE∥DF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEC=∠ECB,
∵CE平分∠DCB,
∴∠DCE=∠ECB,
∴∠DEC=∠DCE,
∴DE=DC,
在△DFC中,CF=3,DF=4,DE=DC=5,
∴DC2=CF2+DF2,
∴△DFC是直角三角形,
∴∠DFC=90°,
∴∠EBC=90°,
在Rt△EBC中,CE=.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵CE=BC,
∴AD=CE,
∴四边形ACED是平行四边形;
(2)解:∵AD=BC,CE=BC,
∴AD=CE=BC,
∵AD∥BC,
∴AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∵CD=BE,
∴∠BDE=90°,BE=2CD=2AB=10,
∴BD===8,
∴△BDE的周长=BD+BE+DE=8+10+6=24.
19.证明:连接BC、AD,如图:
∵BF=DE,
∴BF﹣EF=DE﹣EF
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
20.证明:连接AD、BC,如图所示:
∵AB∥CD,
∴∠BAF=∠DCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
一.选择题
1.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC C.∠A=∠C D.∠B+∠C=180°
2.下列条件中,能判定一个四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等 B.一组对边平行,一组对角相等
C.一组邻边相等,一组对角相等 D.一组对边平行,一组对角互补
3.如图,在四边形ABCD中,对角线AC,BD相交于点O,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC B.AB=CD.AD=BC
C.AD∥BC,∠ABC=∠ADC D.AB=CD,∠ABC=∠ADC
4.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
5.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
6.在等腰△ABC中,AB=AC=5,BC=6,D、E分别为AB、BC边上的中点,连接DE并延长DE到F,使得EF=2ED,连接AE、CF,则CF长为( )
A.4 B.2 C.5 D.3
7.如图,四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
8.如图,在 ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH.有下列结论:①GF⊥BD;②GF=EH;③四边形EGFH是平行四边形;④EG=FH.则正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行
B.一组对边平行,另一组对边相等
C.两条对角线互相平分
D.两组对边分别相等
二.填空题
10.已知O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .
11.在四边形ABCD中,若AB∥CD,BC AD,则四边形ABCD为平行四边形.
12.已知:如图,四边形ABCD中,AB∥CD,AB=CD,AC与BD相交于点O,则图中全等的三角形共有 对.
13.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
三.解答题
14.如图,在△NMB中,BM=8,点A,C,D分别在边MB,BN,MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.
15.如图,AB,CD相交于点E且互相平分,F是BD延长线上一点,若∠FAC=2∠BAC,求证:AC+DF=AF.
16.已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
17.在 ABCD中,E、F分别是AD,BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DF=4,DE=5,求CE的长.
18.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,延长BC到点E,使CE=BC,连接DE.
(1)求证:四边形ACED是平行四边形;
(2)已知AB=5,AC=6,若CD=BE,求△BDE的周长.
19.已知:如图,点E,F在BD上,且AE=CF,BF=DE,∠AEB=∠CFD.求证:AC与BD互相平分.
20.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
参考答案
一.选择题
1.解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
2.解:A、一组对边平行,另一组对边相等,可能是等腰梯形,不一定是平行四边形,故选项A不符合题意;
B、一组对边平行,一组对角相等,可得到两组对边分别平行,为平行四边形,故选项B符合题意;
C、由一组邻边相等,一组对角相等,不能判定一个四边形是平行四边形,故选项C不符合题意;
D、一组对边平行,一组对角互补,可能是等腰梯形,不一定是平行四边形,故选项D不符合题意;
故选:B.
3.解:A、∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=CD.AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BAD=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
D、由AB=CD,∠ABC=∠ADC,不能判定四边形ABCD是平行四边形,故选项D符合题意;
故选:D.
4.解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
5.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
6.解:∵AB=AC=5,BC=6,E为BC边上的中点,
∴AE⊥BC,BE=EC=3,
在Rt△AEC中,AE===4,
∵D、E分别为AB、BC边上的中点,
∴DE∥AC,DE=AC,
∵EF=2ED,
∴EF=AC,
∴四边形EACF为平行四边形,
∴CF=AE=4,
故选:A.
7.解:线段EF与AC交于点O且互相平分,得OA=OC,OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴∠EAO=∠FCO,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴CD=AB,
∴四边形CDEF的周长=CD+DE+EF+CF=CD+AB+DE+AE=CD+AB+AD=6+6+10=22;
故选:C.
8.解:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠GBF=∠HDE,
在△GBF和△HDE中,
,
∴△GBF≌△HDE(SAS),
∴GF=EH,∠BGF=∠DHE,
∴∠FGH=∠EHG,
∴GF∥EH,
∴四边形EGFH是平行四边形,
∴EG=FH,故②③④正确,
∵∠FGH不一定等于90°,
∴GF⊥BD不正确,
故选:C.
9.解:A、一组对边相等且平行的四边形是平行四边形,故本选项不符合题意;
B、一组对边平行且另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形,故本选项符合题意;
C、两条对角线互相平分是平行四边形,故本选项不符合题意;
D、两组对边分别相等的四边形是平行四边形,故本选项不符合题意;
故选:B.
二.填空题
10.解:分三种情况:
①当四边形OABM为平行四边形时,如图1所示:
则BM∥AO,BM=AO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点O向左平移3﹣(﹣1)=4(个)单位,再向上平移1个单位得M的坐标,
∴M(﹣4,1);
②当四边形OAMB为平行四边形时,如图2所示:
则BM∥AO,BM=AO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点B向右平移3个单位,再向上平移1个单位得M的坐标,
∴M(2,3);
③当四边形OBAMM为平行四边形时,如图3所示:
则AB∥MO,AB=MO,
∵O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),
∴把点A向右平移1个单位,再向下平移2个单位得M的坐标,
∴M(4,﹣1);
综上所述,点M的坐标为(﹣4,1)或(2,3)或(4,﹣1);
故答案为:(﹣4,1)或(2,3)或(4,﹣1).
11.解:根据两组对边分别平行的四边形是平行四边形可知:
∵AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
故答案为:∥.
12.解:∵AB∥CD,AB=CD,
∴四边形ABCD为平行四边形,
∴OA=OC,OB=OD,AD=BC,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
同理可得△ACD≌△CAB(SSS);
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
同理可得△AOD≌△COB(SAS);
∴全等三角形有4对,
故答案为:4.
13.解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE=2,AD=BE=1,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°﹣60°﹣30°=90°.
∴EC=2DE=4.
∴BC=BE+EC=1+4=5.
故答案是:5.
三.解答题
14.解:∵DA∥NB,DC∥MB,
∴∠NDC=∠M,四边形ABCD为平行四边形,
∴DC=AB,AD=BC,
∵∠NDC=∠MDA.
∴AD=AM,
∴四边形ABCD的周长=AB+BC+CD+AD=2AM+2AB=2BM=2×8=16.
15.证明:连接AD、BC,
∵AB,CD相交于点E且互相平分,
∴四边形ACBD是平行四边形,
∴AC=BC,AC∥BC,
∴∠BAC=∠ABF,
∵∠FAC=2∠BAC,
∴∠FAB=∠BAC,
∴∠ABF=∠FAB,
∴AF=BF,
∵AC+DF=BD+DF=BF,
∴AC+DF=AF.
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠DCF,AB=CD,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴DE=BF,
∵DE∥BF,
∴四边形BFDE是平行四边形;
(2)∵四边形BFDE是平行四边形,
∴BE=DF,BE∥DF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEC=∠ECB,
∵CE平分∠DCB,
∴∠DCE=∠ECB,
∴∠DEC=∠DCE,
∴DE=DC,
在△DFC中,CF=3,DF=4,DE=DC=5,
∴DC2=CF2+DF2,
∴△DFC是直角三角形,
∴∠DFC=90°,
∴∠EBC=90°,
在Rt△EBC中,CE=.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵CE=BC,
∴AD=CE,
∴四边形ACED是平行四边形;
(2)解:∵AD=BC,CE=BC,
∴AD=CE=BC,
∵AD∥BC,
∴AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∵CD=BE,
∴∠BDE=90°,BE=2CD=2AB=10,
∴BD===8,
∴△BDE的周长=BD+BE+DE=8+10+6=24.
19.证明:连接BC、AD,如图:
∵BF=DE,
∴BF﹣EF=DE﹣EF
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
20.证明:连接AD、BC,如图所示:
∵AB∥CD,
∴∠BAF=∠DCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分.
