人教版九年级上册23.1图形的旋转课件(共17张PPT)
文档属性
| 名称 | 人教版九年级上册23.1图形的旋转课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:18:32 | ||
图片预览



文档简介
(共17张PPT)
23.1 图形的旋转
学习目标(1分钟)
1、掌握图形的旋转的概念及其相关概念
(旋转中心、旋转角、旋转方向).
2、会画出一个图形绕其旋转中心旋转后的图形.
3、能利用旋转设计出美丽的图形.
自学指导一(5分钟)
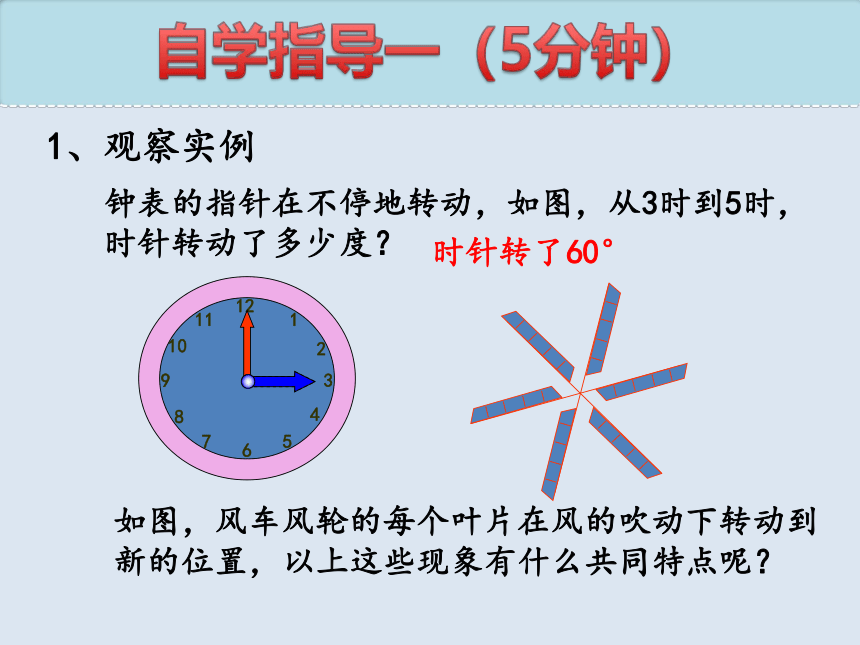
1、观察实例
钟表的指针在不停地转动,如图,从3时到5时,时针转动了多少度?
如图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
时针转了60°
12
6
1
2
3
4
5
7
8
9
10
11
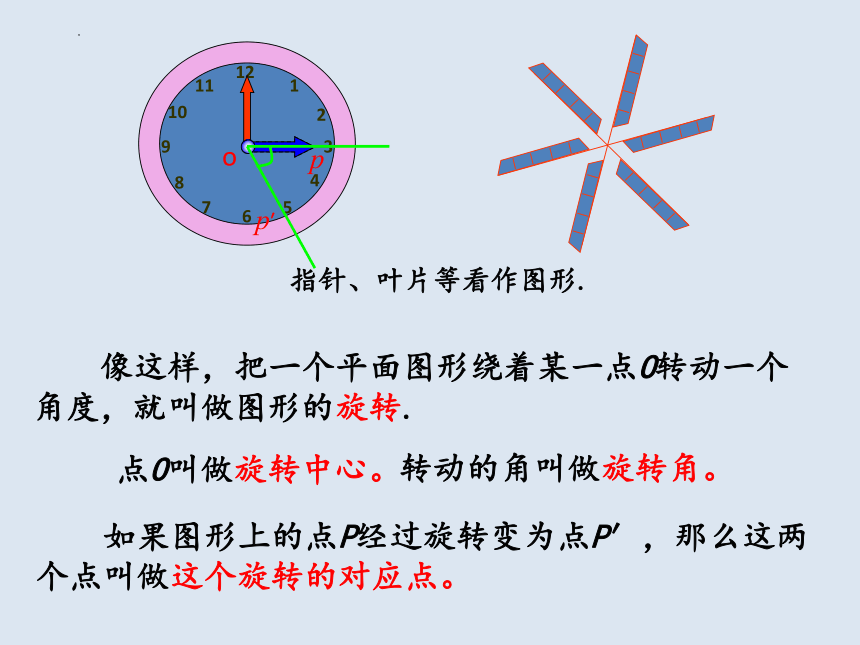
指针、叶片等看作图形.
像这样,把一个平面图形绕着某一点O转动一个角度,就叫做图形的旋转.
点O叫做旋转中心。
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
o
p
p′
转动的角叫做旋转角。
自学检测一(4分钟)
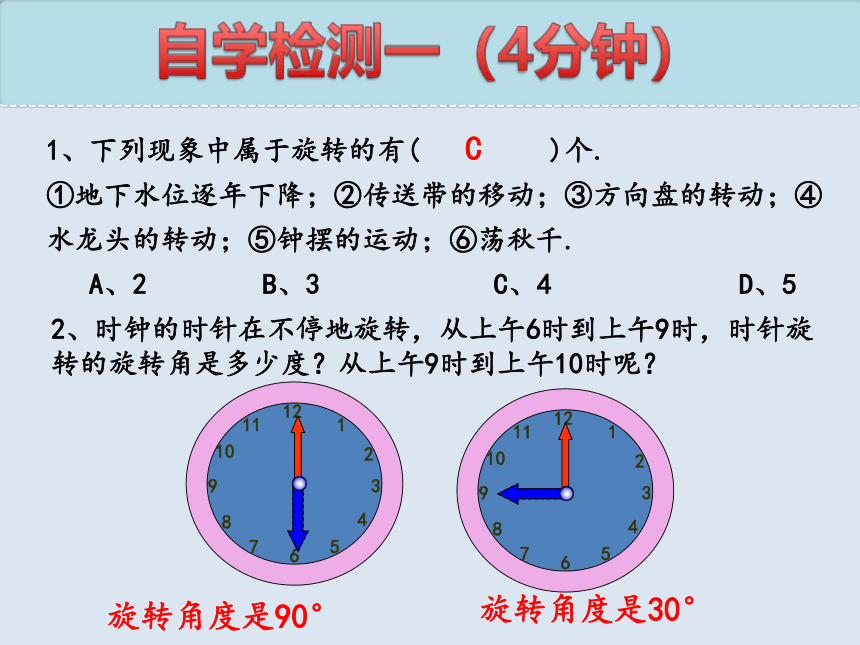
1、下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千.
A、2 B、3 C、4 D、5
2、时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
C
自学指导二(6分钟)
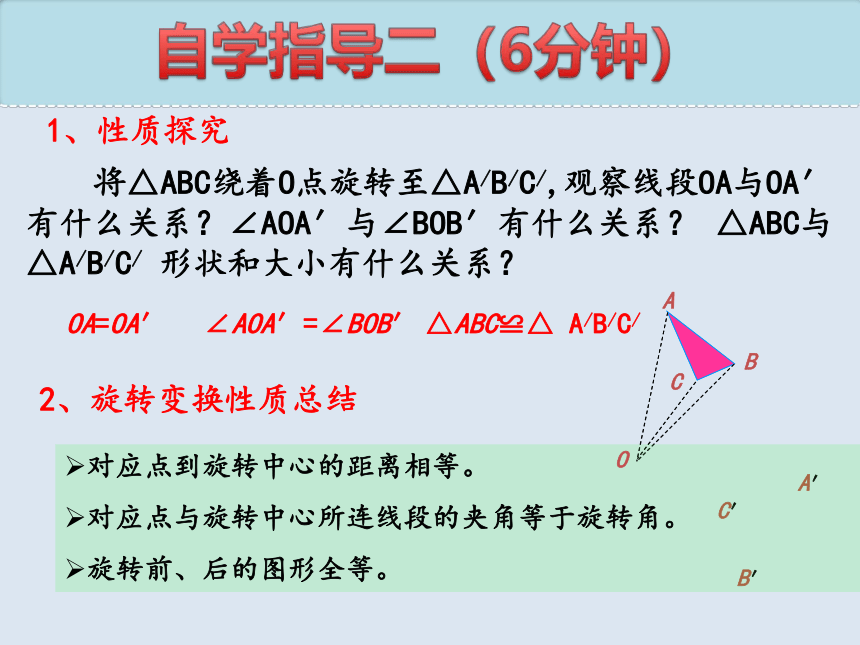
1、性质探究
A
B
C
A′
B′
C′
OA=OA′
∠AOA′=∠BOB′
△ABC≌△ A/B/C/
将△ABC绕着O点旋转至△A/B/C/,观察线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系? △ABC与△A/B/C/ 形状和大小有什么关系?
2、旋转变换性质总结
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
O
自学检测二(6分钟)
1、如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
解:因为点A是旋转中心,所以它的对应点是它本身;
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合;
设点E的对应点为点E′,
因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE .
因此,在CB的延长线上取点E′ ,使BE′ =DE,连接AE ′,则△ABE′为旋转后的图形.
A
B
C
D
E
E′
还有别的办法吗?
3
44°
5
2、
16
45°
45°
67.5 °
3、
课堂小结(3分钟)
旋转变换与平移、轴对称两种变换有哪些共性与区别?
共性:
变换后的图形与原图形全等。
区别主要表现在:
平移的关键是:平移方向和平移的距离;
轴对称的关键是:
对称轴;
旋转的关键是:
旋转中心和旋转角,还要注意旋转方向。
当堂训练(15分钟)
1、已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
B
A
O
A′
B′
2、如图:画出△ABC绕点C按顺时针方向旋转120°后的对应的三角形。
A
B
M
N
D
E
C
120°
120°
3.如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF= cm ,
∠EBF= .
F
C
B
A
D
E
3
90°
4、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A′点位置,若A′C⊥AB,求∠A′的度数。
E
A'
B'
B
C
A
解:∵△ABC绕C点逆时针旋转 30°
∴∠ACA′=30°,∠A= ∠A′
∵A′C⊥AB,
∴∠AEC=∠A′EC=90 °
∴∠A= ∠A′= 60°
A
B
C
D
O
C
旋转时图形上的每个点都绕旋转中心沿相同方向转动相同的角度,但是各点的运动路程不一定相等。
选做题
拓展探究:
已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
G
E
F
O
C
A
B
D
板书设计
旋转变换性质
对应点到旋转中心的距离相等。
对应点与旋转中心所边线段的夹角等于旋转角。
旋转前、后的图形全等。
23.1 图形的旋转
学习目标(1分钟)
1、掌握图形的旋转的概念及其相关概念
(旋转中心、旋转角、旋转方向).
2、会画出一个图形绕其旋转中心旋转后的图形.
3、能利用旋转设计出美丽的图形.
自学指导一(5分钟)
1、观察实例
钟表的指针在不停地转动,如图,从3时到5时,时针转动了多少度?
如图,风车风轮的每个叶片在风的吹动下转动到新的位置,以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
时针转了60°
12
6
1
2
3
4
5
7
8
9
10
11
指针、叶片等看作图形.
像这样,把一个平面图形绕着某一点O转动一个角度,就叫做图形的旋转.
点O叫做旋转中心。
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
o
p
p′
转动的角叫做旋转角。
自学检测一(4分钟)
1、下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千.
A、2 B、3 C、4 D、5
2、时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
12
6
1
2
3
4
5
7
8
9
10
11
12
6
1
2
3
4
5
7
8
9
10
11
旋转角度是90°
旋转角度是30°
C
自学指导二(6分钟)
1、性质探究
A
B
C
A′
B′
C′
OA=OA′
∠AOA′=∠BOB′
△ABC≌△ A/B/C/
将△ABC绕着O点旋转至△A/B/C/,观察线段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系? △ABC与△A/B/C/ 形状和大小有什么关系?
2、旋转变换性质总结
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
O
自学检测二(6分钟)
1、如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
解:因为点A是旋转中心,所以它的对应点是它本身;
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合;
设点E的对应点为点E′,
因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE .
因此,在CB的延长线上取点E′ ,使BE′ =DE,连接AE ′,则△ABE′为旋转后的图形.
A
B
C
D
E
E′
还有别的办法吗?
3
44°
5
2、
16
45°
45°
67.5 °
3、
课堂小结(3分钟)
旋转变换与平移、轴对称两种变换有哪些共性与区别?
共性:
变换后的图形与原图形全等。
区别主要表现在:
平移的关键是:平移方向和平移的距离;
轴对称的关键是:
对称轴;
旋转的关键是:
旋转中心和旋转角,还要注意旋转方向。
当堂训练(15分钟)
1、已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
B
A
O
A′
B′
2、如图:画出△ABC绕点C按顺时针方向旋转120°后的对应的三角形。
A
B
M
N
D
E
C
120°
120°
3.如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF= cm ,
∠EBF= .
F
C
B
A
D
E
3
90°
4、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A′点位置,若A′C⊥AB,求∠A′的度数。
E
A'
B'
B
C
A
解:∵△ABC绕C点逆时针旋转 30°
∴∠ACA′=30°,∠A= ∠A′
∵A′C⊥AB,
∴∠AEC=∠A′EC=90 °
∴∠A= ∠A′= 60°
A
B
C
D
O
C
旋转时图形上的每个点都绕旋转中心沿相同方向转动相同的角度,但是各点的运动路程不一定相等。
选做题
拓展探究:
已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
G
E
F
O
C
A
B
D
板书设计
旋转变换性质
对应点到旋转中心的距离相等。
对应点与旋转中心所边线段的夹角等于旋转角。
旋转前、后的图形全等。
同课章节目录
