沪科版九年级上册21.5反比例函数(第2课时)课件(共26张PPT)
文档属性
| 名称 | 沪科版九年级上册21.5反比例函数(第2课时)课件(共26张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:20:42 | ||
图片预览



文档简介
(共26张PPT)
21.5 反比例函数
第 2 课时
学习目标
反比例函数的图象和性质
准备好了吗?一起去探索吧!
1.进一步熟悉作函数图象的步骤,会用描点法作反比例函数的图象.
2.掌握反比例函数的图象和性质,并会应用.
3.通过观察图象分析其性质,培养学生的探究、归纳及概括的能力.
4.让学生尝试发现反比例函数的图象的特点,学会由具体到抽象,由特殊到一般地探索事物规律的方法.
一次函数的图象
二次函数的图象
回顾
回顾
反比例函数的图象
描点法
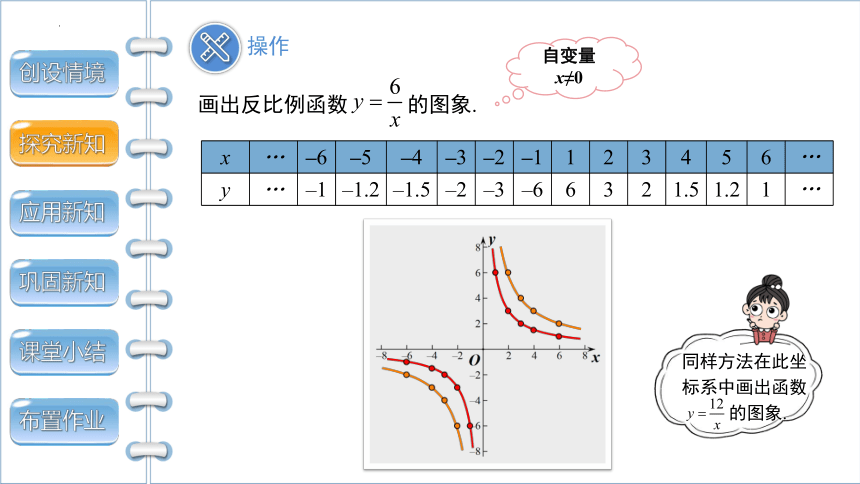
x … –6 –5 –4 –3 –2 –1 1 2 3 4 5 6 …
y … –1 –1.2 –1.5 –2 –3 –6 6 3 2 1.5 1.2 1 …
画出反比例函数 的图象.
自变量x≠0
同样方法在此坐标系中画出函数
的图象.
操作
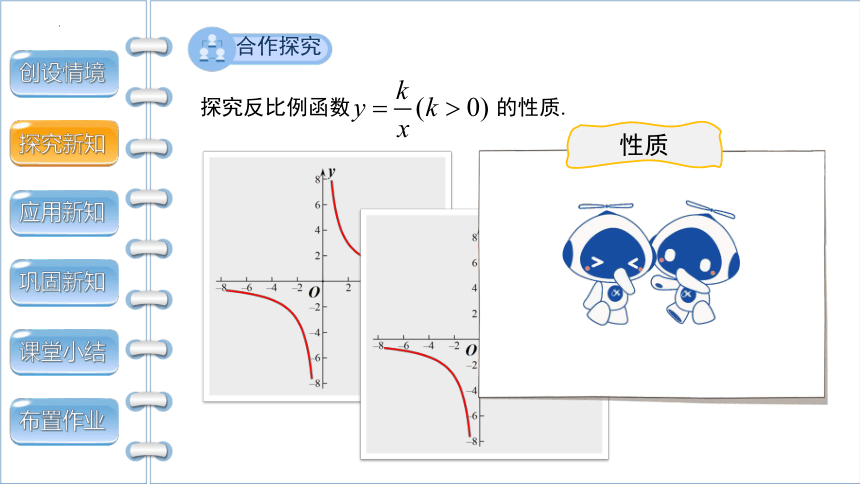
探究反比例函数 的性质.
性质
合作探究
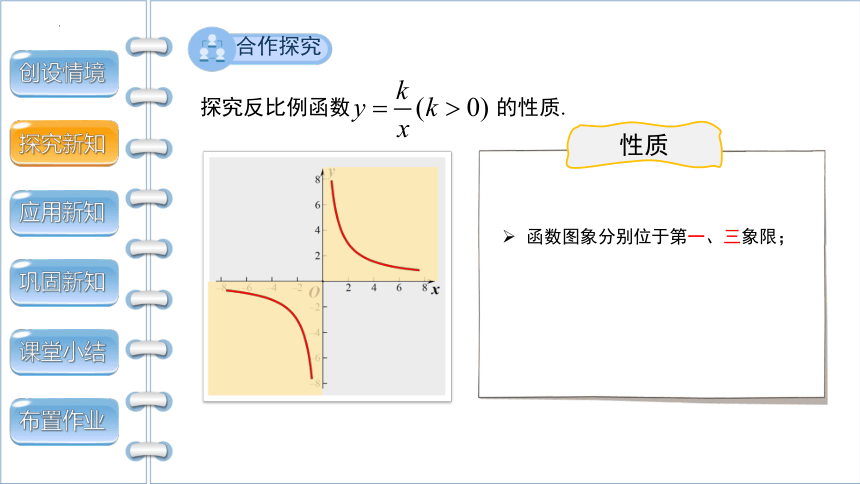
性质
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
合作探究
性质
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
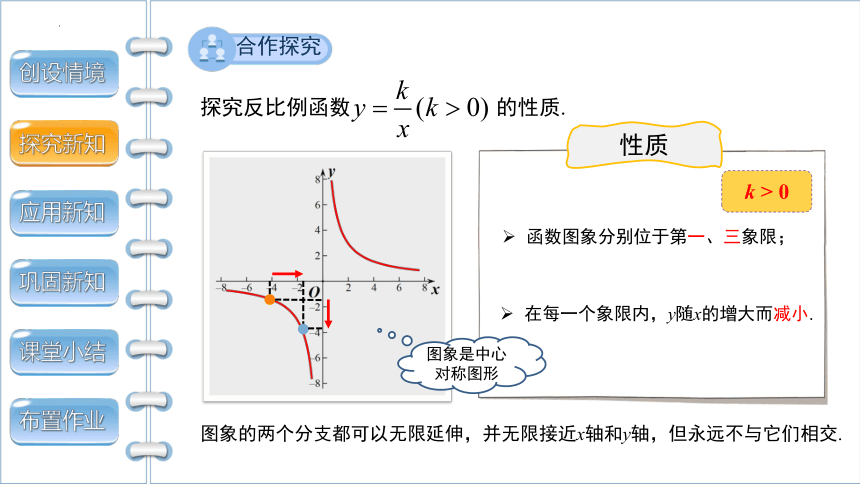
合作探究
性质
k > 0
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
图象的两个分支都可以无限延伸,并无限接近x轴和y轴,但永远不与它们相交.
合作探究
图象是中心对称图形
x … –6 –5 –4 –3 –2 –1 1 2 3 4 5 6 …
y … 1 1.2 1.5 2 3 6 –6 –3 –2 –1.5 –1.2 –1 …
画出反比例函数 的图象.
同样方法在此坐标系中画出函数
的图象.
操作
合作探究
性质
探究反比例函数 的性质.
合作探究
探究反比例函数 的性质.
性质
函数图象分别位于第二、四象限;
合作探究
探究反比例函数 的性质
性质
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
合作探究
探究反比例函数 的性质.
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
图象的两个分支都可以无限延伸,并无限接近x轴和y轴,但永远不与它们相交.
图象是中心对称图形
思考
观察并对比函数 与 的图象,你能就k>0,和k<0
两种情况,分别总结反比例函数 (k为常数,且k≠0)的性质吗?
反比例函数
双曲线
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
归纳
图象是中心对称图形
典型例题
例1 如图所示的图象对应的函数解析式为( )
A.
B.
C.
D.
D
双曲线
k<0
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
B
抢答
随堂练习
1.填空:
(1)对于函数 ,自变量x的取值范围是 ,
当x>0时,y 0;当x<0时,y 0;
(2)对于函数 ,当x>0时,函数y随x的增大而 ;
当x<0时,函数y随x的增大而 ;
(3)反比例函数 的图象与直线y=2x交于两点,这两点
的坐标分别是( , )和( , ).
x≠ 0
<
>
增大
增大
2
1
–2
–1
抢答
随堂练习
2.下列反比例函数中,其图象的一个分支
一定在第三象限的是( )
(A)
(B)
(C)
(D)
(m为常数,且m≠-2)
(a为常数,且a≠±1)
C
k > 0
抢答
随堂练习
3.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数
的图象上,且x1”或“<”).
<
x1
x2
y1
y2
P1
P2
反比例函数的图象和性质
图象:
性质:
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
教科书第48页练习
第2题
再见
21.5 反比例函数
第 2 课时
学习目标
反比例函数的图象和性质
准备好了吗?一起去探索吧!
1.进一步熟悉作函数图象的步骤,会用描点法作反比例函数的图象.
2.掌握反比例函数的图象和性质,并会应用.
3.通过观察图象分析其性质,培养学生的探究、归纳及概括的能力.
4.让学生尝试发现反比例函数的图象的特点,学会由具体到抽象,由特殊到一般地探索事物规律的方法.
一次函数的图象
二次函数的图象
回顾
回顾
反比例函数的图象
描点法
x … –6 –5 –4 –3 –2 –1 1 2 3 4 5 6 …
y … –1 –1.2 –1.5 –2 –3 –6 6 3 2 1.5 1.2 1 …
画出反比例函数 的图象.
自变量x≠0
同样方法在此坐标系中画出函数
的图象.
操作
探究反比例函数 的性质.
性质
合作探究
性质
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
合作探究
性质
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
合作探究
性质
k > 0
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
探究反比例函数 的性质.
图象的两个分支都可以无限延伸,并无限接近x轴和y轴,但永远不与它们相交.
合作探究
图象是中心对称图形
x … –6 –5 –4 –3 –2 –1 1 2 3 4 5 6 …
y … 1 1.2 1.5 2 3 6 –6 –3 –2 –1.5 –1.2 –1 …
画出反比例函数 的图象.
同样方法在此坐标系中画出函数
的图象.
操作
合作探究
性质
探究反比例函数 的性质.
合作探究
探究反比例函数 的性质.
性质
函数图象分别位于第二、四象限;
合作探究
探究反比例函数 的性质
性质
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
合作探究
探究反比例函数 的性质.
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
图象的两个分支都可以无限延伸,并无限接近x轴和y轴,但永远不与它们相交.
图象是中心对称图形
思考
观察并对比函数 与 的图象,你能就k>0,和k<0
两种情况,分别总结反比例函数 (k为常数,且k≠0)的性质吗?
反比例函数
双曲线
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
归纳
图象是中心对称图形
典型例题
例1 如图所示的图象对应的函数解析式为( )
A.
B.
C.
D.
D
双曲线
k<0
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
典型例题
例2 若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
B
抢答
随堂练习
1.填空:
(1)对于函数 ,自变量x的取值范围是 ,
当x>0时,y 0;当x<0时,y 0;
(2)对于函数 ,当x>0时,函数y随x的增大而 ;
当x<0时,函数y随x的增大而 ;
(3)反比例函数 的图象与直线y=2x交于两点,这两点
的坐标分别是( , )和( , ).
x≠ 0
<
>
增大
增大
2
1
–2
–1
抢答
随堂练习
2.下列反比例函数中,其图象的一个分支
一定在第三象限的是( )
(A)
(B)
(C)
(D)
(m为常数,且m≠-2)
(a为常数,且a≠±1)
C
k > 0
抢答
随堂练习
3.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数
的图象上,且x1
<
x1
x2
y1
y2
P1
P2
反比例函数的图象和性质
图象:
性质:
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
教科书第48页练习
第2题
再见
