沪教版九年级上册21.4二次函数的应用(第2课时)课件(共20张PPT)
文档属性
| 名称 | 沪教版九年级上册21.4二次函数的应用(第2课时)课件(共20张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:30:08 | ||
图片预览



文档简介
(共20张PPT)
21.4 二次函数的应用
第2课时
准备好了吗?一起去探索吧!
学习目标
1.能根据实际问题建立合适的平面直角坐标系,找出数量关系;
2.能建立二次函数解析式,并能应用二次函数的相关性质解决实际问题;
3.从“数”(解析式)和“形”(图象)的角度理解二次函数与实际问题之间的联系,体会“数形结合”的思想,以及建模的转化思想;
4. 经历了建模来解决实际生活中的问题,体会函数知识的实际应用价值,感受数学与人类生活的密切联系.
桥梁建筑等问题
观察思考
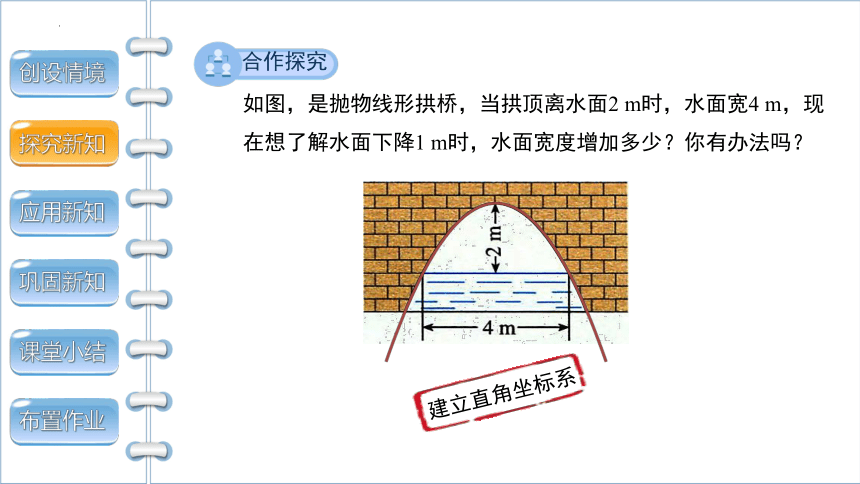
观察下列建筑构成的形状,可近似看作什么?
抛物线
你知道如何求这些抛物线的解析式吗?
合作探究
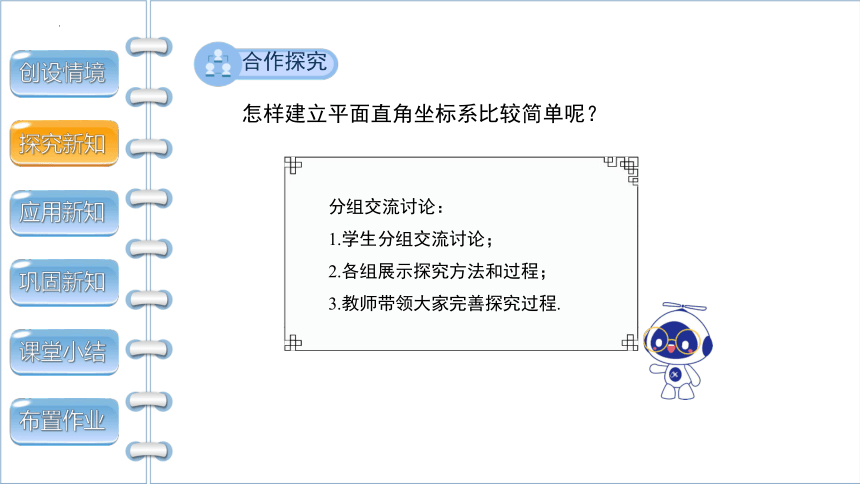
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,现在想了解水面下降1 m时,水面宽度增加多少?你有办法吗?
建立直角坐标系
怎样建立平面直角坐标系比较简单呢?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示探究方法和过程;
3.教师带领大家完善探究过程.
合作探究
交流
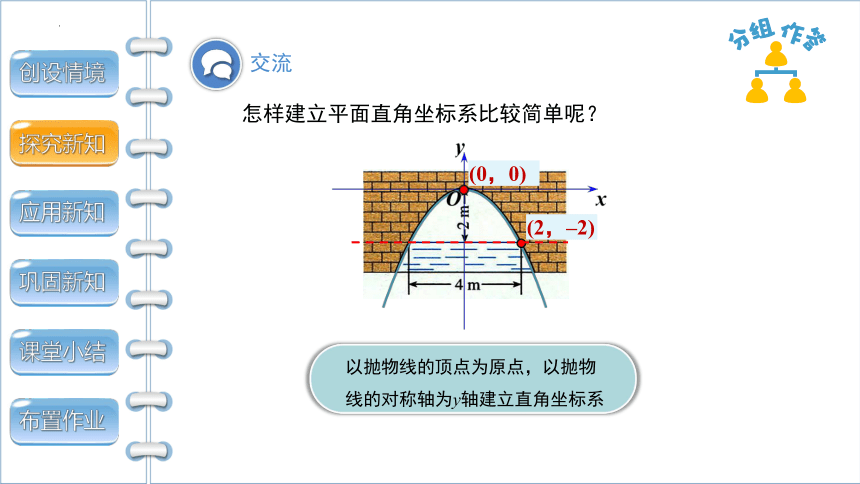
怎样建立平面直角坐标系比较简单呢?
(2,–2)
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系
(0,0)
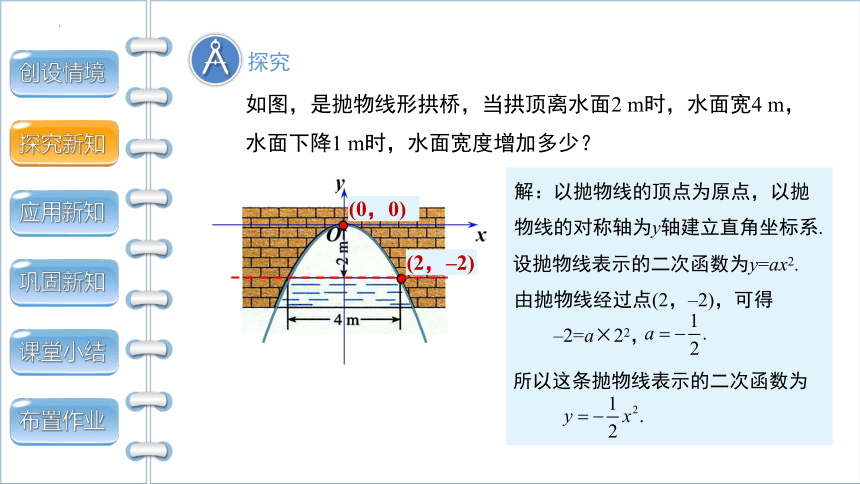
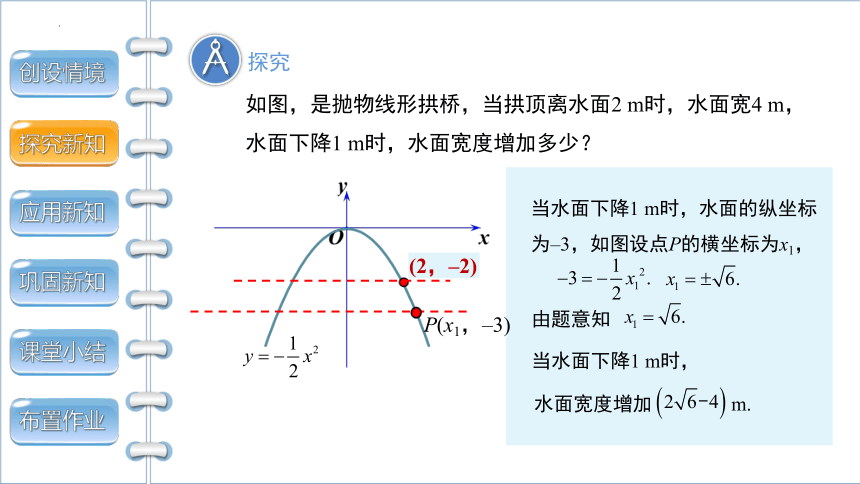
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m时,水面宽度增加多少?
探究
解:以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,–2),可得
–2=a×22,
所以这条抛物线表示的二次函数为
(2,–2)
(0,0)
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m时,水面宽度增加多少?
探究
(2,–2)
当水面下降1 m时,水面的纵坐标为–3,如图设点P的横坐标为x1,
由题意知
水面宽度增加 m.
当水面下降1 m时,
P(x1,–3)
归纳
建立二次函数模型解决桥梁建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 根据二次函数的图象和性质求解,并解决实际问题.
【例】如图(1),悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图(2),求这条抛物线对应的函数表达式;
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
典型例题
(1)
450
450
(0,0.5)
(450,81.5)
(2)
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图(2),求这条抛物线对应的函数表达式;
典型例题
450
450
(0,0.5)
(450,81.5)
(2)
解:(1)根据题意,得抛物线的顶点坐标为(0,0.5),对称轴为y轴,设抛物线对应的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得 81.5=a·4502+0.5.
解方程,得
答:所求抛物线对应的函数表达式为
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
典型例题
450
450
(0,0.5)
(450,81.5)
(2)
(2)当x=450 100=350(m)时,得
答:距离桥两端主塔分别为100 m,50 m处垂直钢索的长分别为49.5 m,64.5 m.
当x=450 50=4000(m)时,得
随堂练习
1.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16 m,跨度为40 m,现把它的示意图放在坐标系中,则抛物线的解析式为( )
A.
B.
C.
D.
C
随堂练习
2.某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高各有一个壁灯,两壁灯之间的水平距离为6 m,如图所示,则厂门的高为(水泥建筑物厚度忽略不计,精确到0.1 m) ( )
A. 6.9 m B. 7.0 m C. 7.1 m D. 6.8 m
A
随堂练习
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
C
D
A
B
解:(1)建立如图所示的直角坐标系,
则点E(0,3),A(3,0),B(– 3,0)
设抛物线的解析式为y=ax2+k.
把点E,点A坐标代入到抛物线的解析式中.
则
解得
所以
E
随堂练习
C
D
A
B
E
当y=0.5时,
故水面宽度CD为 m.
所以 (m)
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
随堂练习
C
D
A
B
E
(2)当x=1时,
所以这艘游船能通过.
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
建立二次函数模型解决桥梁建筑类实际问题的一般步骤:
二次函数的应用
桥梁建筑类实际问题与二次函数的联系:
实际问题
二次函数
建立模型
二次函数的图象和性质
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 根据二次函数的图象和性质求解,并解决实际问题.
教科书第38页
练习第1,2题
再见
21.4 二次函数的应用
第2课时
准备好了吗?一起去探索吧!
学习目标
1.能根据实际问题建立合适的平面直角坐标系,找出数量关系;
2.能建立二次函数解析式,并能应用二次函数的相关性质解决实际问题;
3.从“数”(解析式)和“形”(图象)的角度理解二次函数与实际问题之间的联系,体会“数形结合”的思想,以及建模的转化思想;
4. 经历了建模来解决实际生活中的问题,体会函数知识的实际应用价值,感受数学与人类生活的密切联系.
桥梁建筑等问题
观察思考
观察下列建筑构成的形状,可近似看作什么?
抛物线
你知道如何求这些抛物线的解析式吗?
合作探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,现在想了解水面下降1 m时,水面宽度增加多少?你有办法吗?
建立直角坐标系
怎样建立平面直角坐标系比较简单呢?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示探究方法和过程;
3.教师带领大家完善探究过程.
合作探究
交流
怎样建立平面直角坐标系比较简单呢?
(2,–2)
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系
(0,0)
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m时,水面宽度增加多少?
探究
解:以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,–2),可得
–2=a×22,
所以这条抛物线表示的二次函数为
(2,–2)
(0,0)
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m时,水面宽度增加多少?
探究
(2,–2)
当水面下降1 m时,水面的纵坐标为–3,如图设点P的横坐标为x1,
由题意知
水面宽度增加 m.
当水面下降1 m时,
P(x1,–3)
归纳
建立二次函数模型解决桥梁建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 根据二次函数的图象和性质求解,并解决实际问题.
【例】如图(1),悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图(2),求这条抛物线对应的函数表达式;
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
典型例题
(1)
450
450
(0,0.5)
(450,81.5)
(2)
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图(2),求这条抛物线对应的函数表达式;
典型例题
450
450
(0,0.5)
(450,81.5)
(2)
解:(1)根据题意,得抛物线的顶点坐标为(0,0.5),对称轴为y轴,设抛物线对应的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得 81.5=a·4502+0.5.
解方程,得
答:所求抛物线对应的函数表达式为
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
典型例题
450
450
(0,0.5)
(450,81.5)
(2)
(2)当x=450 100=350(m)时,得
答:距离桥两端主塔分别为100 m,50 m处垂直钢索的长分别为49.5 m,64.5 m.
当x=450 50=4000(m)时,得
随堂练习
1.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16 m,跨度为40 m,现把它的示意图放在坐标系中,则抛物线的解析式为( )
A.
B.
C.
D.
C
随堂练习
2.某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高各有一个壁灯,两壁灯之间的水平距离为6 m,如图所示,则厂门的高为(水泥建筑物厚度忽略不计,精确到0.1 m) ( )
A. 6.9 m B. 7.0 m C. 7.1 m D. 6.8 m
A
随堂练习
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
C
D
A
B
解:(1)建立如图所示的直角坐标系,
则点E(0,3),A(3,0),B(– 3,0)
设抛物线的解析式为y=ax2+k.
把点E,点A坐标代入到抛物线的解析式中.
则
解得
所以
E
随堂练习
C
D
A
B
E
当y=0.5时,
故水面宽度CD为 m.
所以 (m)
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
随堂练习
C
D
A
B
E
(2)当x=1时,
所以这艘游船能通过.
3.河上有一座抛物线形隧道(下图为示意图) ,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船的宽度(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
建立二次函数模型解决桥梁建筑类实际问题的一般步骤:
二次函数的应用
桥梁建筑类实际问题与二次函数的联系:
实际问题
二次函数
建立模型
二次函数的图象和性质
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 根据二次函数的图象和性质求解,并解决实际问题.
教科书第38页
练习第1,2题
再见
