沪教版九年级上册21.4二次函数的应用(第1课时)课件(共17张PPT)
文档属性
| 名称 | 沪教版九年级上册21.4二次函数的应用(第1课时)课件(共17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:31:49 | ||
图片预览


文档简介
(共17张PPT)
21.4 二次函数的应用
第1课时
准备好了吗?一起去探索吧!
学习目标
1.能根据具体几何问题中的数量关系,列出二次函数解析式,并能应用二次函数的相关性质解决面积问题;
2.经历运用二次函数的性质解决实际问题的过程,体会“数形结合”的思想;
3.通过建立实际问题与二次函数的联系,提高学生数学建模的能力;
4.通过用二次函数解决实际生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系.
面
积问题
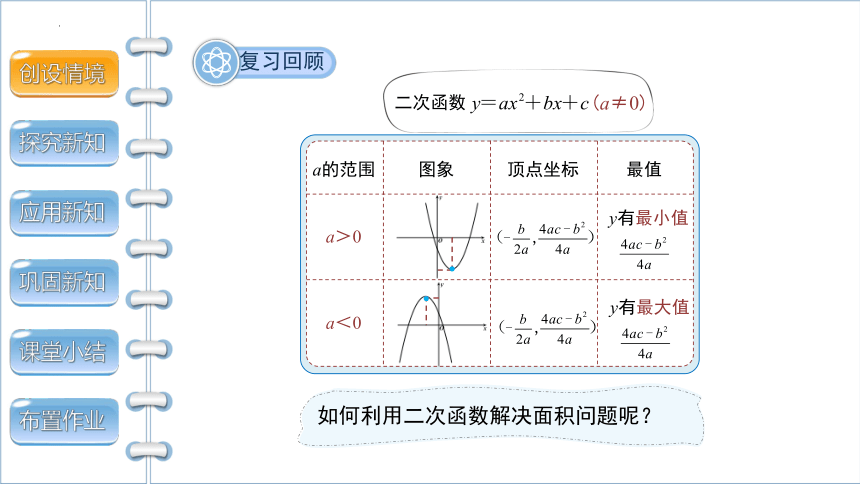
观察思考
二次函数
还记得如何求二次函数的最值吗?
最大高度
最大高度
二次函数的
最值
观察物体运动形成的路线,说一说与什么函数图象类似?
二次函数
a的范围
图象
最值
顶点坐标
a>0
a<0
( , )
y有最小值
( , )
y有最大值
(a≠0)
如何利用二次函数解决面积问题呢?
复习回顾
你能画一个周长为60 cm的矩形吗?
这些矩形的面积一定相等吗?
不一定
合作探究
当周长为60 cm时,你能画出一个面积最大的矩形吗?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示探究方法和过程;
3.教师带领大家完善探究过程.
合作探究
x
30 x
S矩形 x(30 x)
S矩形 x 30x
S最大 –15 30 15 225
15 cm
15 cm
225 cm
求S的最大值
对应的函数值
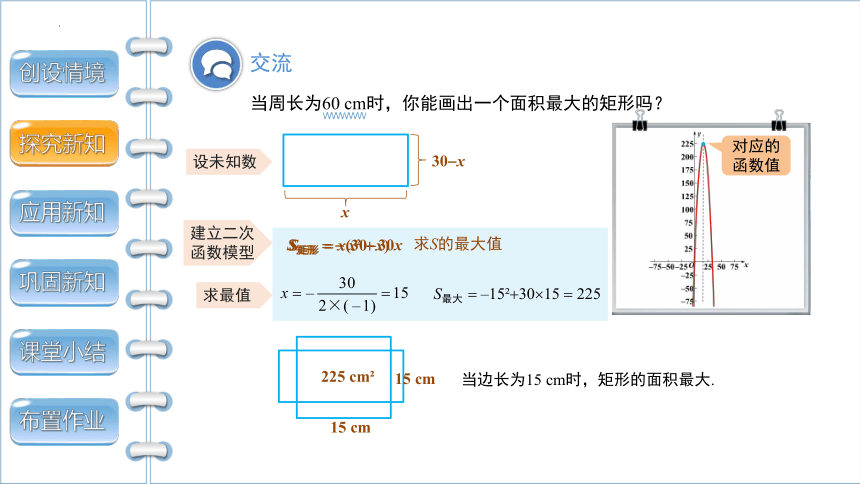
交流
当周长为60 cm时,你能画出一个面积最大的矩形吗?
设未知数
建立二次函数模型
求最值
当边长为15 cm时,矩形的面积最大.
利用二次函数求几何图形面积的最值问题的一般步骤:
设图形的一边长为自变量,所求面积为因变量;
利用题目中的已知条件和学过的有关数学公式建立二次
函数模型,并指明自变量的范围;
利用二次函数的性质求最值.
1
2
3
归纳
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
典型例题
分析:首先要找出围成的水面面积与边长之间的关系.
水面面积 = 一条边长×另一条边长
x m
(20–x)m
S m
S=x(20–x)
S= –x2 +20x
x的取值有什么限制吗?
(0<x<20)
典型例题
解:设围成的矩形水面的一边长为x m,那么,矩形水面的另一边长应为(20 x) m.若它的面积是S m2,则有
S=x(20 x)
将这个函数表达式配方,得:
S= (x 10) +100 (0<x<20).
这个函数的图象是一条开口向下抛物线中的一段,如图,它的顶点坐标是(10,100).
S/m2
x/m
(10,100)
图中为何有两个空心点?
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
典型例题
S/m2
x/m
(10,100)
当x=10时,函数取得最大值,即 S最大=100(m2).
此时,另一边长=20 10=10(m).
答:当围成的矩形水面边长都为10 m时,它的面积最大为100 m2.
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
随堂练习
1.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
解析:设直角三角形的一直角边长为x cm,那么,另一直角边长应为(20 x) cm.若它的面积是S cm2,则有
S= x(20 x)
将这个函数表达式配方,得:
S= (x 10) +50 (0<x<20).
当x=10时,函数取得最大值,即 S最大=50(cm2).
随堂练习
2.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24 m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 .
144 m2
解析:设矩形的一边长为x m,那么,另一边长应为(24 x) m.若它的面积是S m2,则有
S= x(24 x)
将这个函数表达式配方,得:
S= (x 12) +144 (0<x<24).
当x=12时,函数取得最大值,即 S最大=144(m2).
随堂练习
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
所以,它们的面积和最小为450 cm2.
二次函数的最值:
二次函数的应用
(a≠0)
求面积最值等实际问题与二次函数的联系:
实际问题
二次函数
建立模型
二次函数的最值
教科书第36页
练习第1,2题
再见
21.4 二次函数的应用
第1课时
准备好了吗?一起去探索吧!
学习目标
1.能根据具体几何问题中的数量关系,列出二次函数解析式,并能应用二次函数的相关性质解决面积问题;
2.经历运用二次函数的性质解决实际问题的过程,体会“数形结合”的思想;
3.通过建立实际问题与二次函数的联系,提高学生数学建模的能力;
4.通过用二次函数解决实际生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系.
面
积问题
观察思考
二次函数
还记得如何求二次函数的最值吗?
最大高度
最大高度
二次函数的
最值
观察物体运动形成的路线,说一说与什么函数图象类似?
二次函数
a的范围
图象
最值
顶点坐标
a>0
a<0
( , )
y有最小值
( , )
y有最大值
(a≠0)
如何利用二次函数解决面积问题呢?
复习回顾
你能画一个周长为60 cm的矩形吗?
这些矩形的面积一定相等吗?
不一定
合作探究
当周长为60 cm时,你能画出一个面积最大的矩形吗?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示探究方法和过程;
3.教师带领大家完善探究过程.
合作探究
x
30 x
S矩形 x(30 x)
S矩形 x 30x
S最大 –15 30 15 225
15 cm
15 cm
225 cm
求S的最大值
对应的函数值
交流
当周长为60 cm时,你能画出一个面积最大的矩形吗?
设未知数
建立二次函数模型
求最值
当边长为15 cm时,矩形的面积最大.
利用二次函数求几何图形面积的最值问题的一般步骤:
设图形的一边长为自变量,所求面积为因变量;
利用题目中的已知条件和学过的有关数学公式建立二次
函数模型,并指明自变量的范围;
利用二次函数的性质求最值.
1
2
3
归纳
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
典型例题
分析:首先要找出围成的水面面积与边长之间的关系.
水面面积 = 一条边长×另一条边长
x m
(20–x)m
S m
S=x(20–x)
S= –x2 +20x
x的取值有什么限制吗?
(0<x<20)
典型例题
解:设围成的矩形水面的一边长为x m,那么,矩形水面的另一边长应为(20 x) m.若它的面积是S m2,则有
S=x(20 x)
将这个函数表达式配方,得:
S= (x 10) +100 (0<x<20).
这个函数的图象是一条开口向下抛物线中的一段,如图,它的顶点坐标是(10,100).
S/m2
x/m
(10,100)
图中为何有两个空心点?
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
典型例题
S/m2
x/m
(10,100)
当x=10时,函数取得最大值,即 S最大=100(m2).
此时,另一边长=20 10=10(m).
答:当围成的矩形水面边长都为10 m时,它的面积最大为100 m2.
【例】某水产养殖户用长40 m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?最大面积是多少平方米?
随堂练习
1.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
解析:设直角三角形的一直角边长为x cm,那么,另一直角边长应为(20 x) cm.若它的面积是S cm2,则有
S= x(20 x)
将这个函数表达式配方,得:
S= (x 10) +50 (0<x<20).
当x=10时,函数取得最大值,即 S最大=50(cm2).
随堂练习
2.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24 m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 .
144 m2
解析:设矩形的一边长为x m,那么,另一边长应为(24 x) m.若它的面积是S m2,则有
S= x(24 x)
将这个函数表达式配方,得:
S= (x 12) +144 (0<x<24).
当x=12时,函数取得最大值,即 S最大=144(m2).
随堂练习
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
所以,它们的面积和最小为450 cm2.
二次函数的最值:
二次函数的应用
(a≠0)
求面积最值等实际问题与二次函数的联系:
实际问题
二次函数
建立模型
二次函数的最值
教科书第36页
练习第1,2题
再见
