人教版九年级上册21.2.4一元二次方程的根与系数的关系课件(共22张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.4一元二次方程的根与系数的关系课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 378.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:33:01 | ||
图片预览







文档简介
(共22张PPT)
21.2一元二次方程的根
与系数的关系
第21章 一元二次方程
1、一元二次方程的一般形式?
ax2+bx+c=0(a≠0)
2、一元二次方程有实数根的条件是什么?
△=b2-4ac≥0
3、当△>0,△=0,△<0, Δ≥0根的情况如何?
复习回顾 (2分钟)
当Δ>0时,方程有两个不相等的实数根;
当Δ=0时,方程有两个相等的实数根;
当Δ<0时,方程没有实数根;
当Δ≥0时,方程有实数根;
4、一元二次方程的求根公式是什么?
学习目标(1分钟)
1. 了解一元二次方程的根与系数的关系;
2.能利用一元二次方程的根与系数关系解决一些综合性问题.
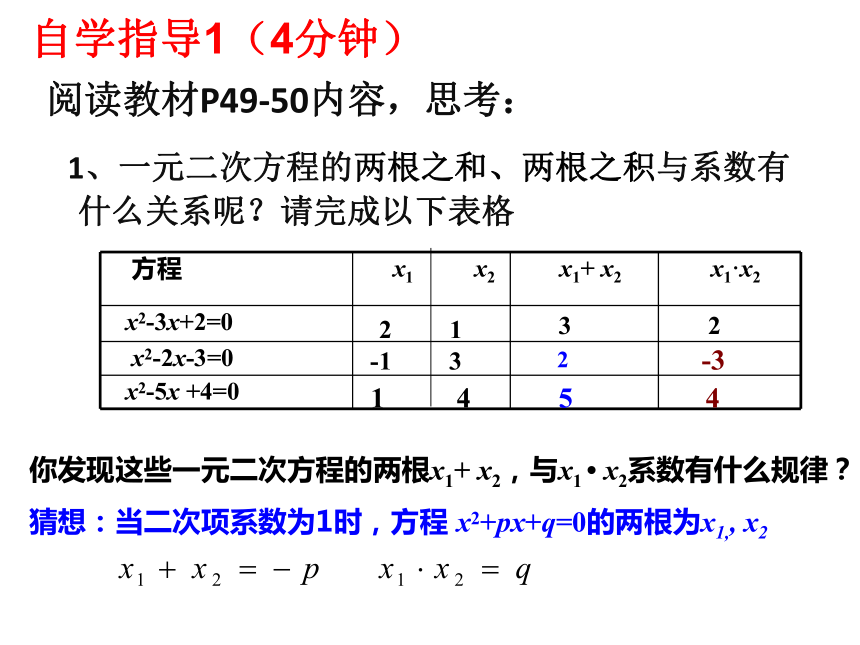
阅读教材P49-50内容,思考:
1、一元二次方程的两根之和、两根之积与系数有什么关系呢?请完成以下表格
自学指导1(4分钟)
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
你发现这些一元二次方程的两根x1+ x2,与x1 x2系数有什么规律?猜想:当二次项系数为1时,方程 x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
方 程
-2
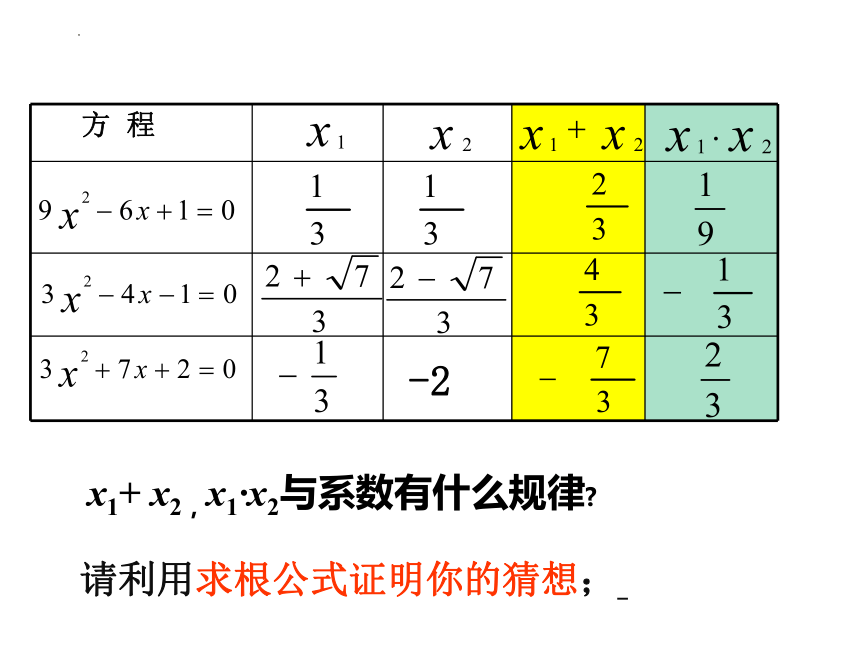
x1+ x2,x1 x2与系数有什么规律
请利用求根公式证明你的猜想;
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
自学检测1(3分钟)
根据根与系数的关系写出下列方程的两根之和与两根之积(方程两根为x1,x2、k是常数)
(1)2x2-3x-1=0 x1+x2 = ___ x1x2= ___
(2)x2+7x=-6 x1+x2= ___ x1x2= ___
(3)5x2+kx-6=0 x1+x2= ___ x1x2= ___
-7
6
b2 -4ac=
举一反三
A
1. 若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )
A. -10 B. 10 C. -16 D. 16
2. 若一元二次方程x2+4x-3=0的两根为x1,x2 ,则x1·x2的值是( )
A. 4 B. -4 C. 3 D. -3
3. 若方程x2-2x-1=0 的两根分别为x1,x2,则x1+x2-x1x2 的值为 .
D
3
认真阅看下面例题,掌握其解题的方法.
自学指导2(4分钟)
例2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ___,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
4
1
2X1X2
14
X1+X2
12
1.已知方程的 一个根是2,求它的另一个根及K的值
自学检测2(8分钟)
2. 已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1.X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
易错点
点拨:(4分钟)
在使用根与系数的关系时,注意不要忽视前提条件
利用根与系数的关系,求一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2的
(1)平方和 :
(2)倒数和 :
(3)差的绝对值:
△=b2-4ac≥0
易错点:
课堂小结 (2分钟)
在方程ax2+bx+c=0(a≠0)中, a、b、c有哪些作用?
1、求根公式:
2、韦达定理:
1.下列方程的两根和与两根积各是多少?
2.已知两个数的和是1,积是-2,则这两个数是_______
3.若一个矩形的长和宽是一元二次方程 x -10x+20=0的
两根,则这个矩形的周长是_____ ,面积是_____
4.若方程2x -x=3的两根为 则
当堂训练(13分钟)
2和-1
20
20
5.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,求m+n的值.
解:∵关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,
∴-2+4=-m,-2×4=n,
解得m=-2,n=-8,
∴m+n=-10.
6. 方程 有一个正根,一个负根,求m的取值范围。
解:由已知可得:
△=
{
∴因此m的取值范围是 0解得
{
m>0
m-1<0
7. 方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
②∵两根互为倒数 m2 6m 5,
∴两根之积2m 1 1 ,∴ m 1且 0,
∴m 1时,方程的两根互为倒数.
③∵方程一根为0,
∴两根之积2m 1 0得 且 0,
∴ 时,方程有一根为零.
解: (m 1)2 4(2m 1) m2 6m 5
①∵两根互为相反数
∴两根之和m 1 0,m 1,且 0
∴m 1时,方程的两根互为相反数.
7. 方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
选做题
设x1,x2是方程x2-x-2 013=0的两实数根,则x13 +2 014x2-2 013= .
解 ∵x2-x-2 013=0,∴x2=x+2 013.
又∵x1,x2是方程x2-x-2 013=0的两实数根,
∴x1+x2=1,∴x13+2 014x2-2 013
=x1·x12+2 013x2+x2-2 013
=x1·(x1+2 013)+2 013x2+x2-2 013
=(x1+2 013)+2 013x1+2 013x2+x2-2 013
=x1+x2+2 013(x1+x2)+2 013-2 013
=1+2 013
=2 014.
答案 2 014
板书设计
2.5一元二次方程的根
与系数的关系
求根公式:
根与系数的关系:
公式推导:
设x1 、x2是一元二次方程ax2+bx+c=0 (a≠0)的两个根,
则x1=
X2=
负号千万别丢掉!
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
例:利用根与系数的关系,
求下列方程的两根之和、两根之积:
x2 +7x+6=0
解:这里a=1,b=7,c=6.
b2-4ac=7-4×1×6=49-24=25>0
∴方程有两个实数根。
∴x1+x2=-7,x1x2=6
为什么要加上这一步?
21.2一元二次方程的根
与系数的关系
第21章 一元二次方程
1、一元二次方程的一般形式?
ax2+bx+c=0(a≠0)
2、一元二次方程有实数根的条件是什么?
△=b2-4ac≥0
3、当△>0,△=0,△<0, Δ≥0根的情况如何?
复习回顾 (2分钟)
当Δ>0时,方程有两个不相等的实数根;
当Δ=0时,方程有两个相等的实数根;
当Δ<0时,方程没有实数根;
当Δ≥0时,方程有实数根;
4、一元二次方程的求根公式是什么?
学习目标(1分钟)
1. 了解一元二次方程的根与系数的关系;
2.能利用一元二次方程的根与系数关系解决一些综合性问题.
阅读教材P49-50内容,思考:
1、一元二次方程的两根之和、两根之积与系数有什么关系呢?请完成以下表格
自学指导1(4分钟)
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
你发现这些一元二次方程的两根x1+ x2,与x1 x2系数有什么规律?猜想:当二次项系数为1时,方程 x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
方 程
-2
x1+ x2,x1 x2与系数有什么规律
请利用求根公式证明你的猜想;
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
自学检测1(3分钟)
根据根与系数的关系写出下列方程的两根之和与两根之积(方程两根为x1,x2、k是常数)
(1)2x2-3x-1=0 x1+x2 = ___ x1x2= ___
(2)x2+7x=-6 x1+x2= ___ x1x2= ___
(3)5x2+kx-6=0 x1+x2= ___ x1x2= ___
-7
6
b2 -4ac=
举一反三
A
1. 若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )
A. -10 B. 10 C. -16 D. 16
2. 若一元二次方程x2+4x-3=0的两根为x1,x2 ,则x1·x2的值是( )
A. 4 B. -4 C. 3 D. -3
3. 若方程x2-2x-1=0 的两根分别为x1,x2,则x1+x2-x1x2 的值为 .
D
3
认真阅看下面例题,掌握其解题的方法.
自学指导2(4分钟)
例2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ___,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
4
1
2X1X2
14
X1+X2
12
1.已知方程的 一个根是2,求它的另一个根及K的值
自学检测2(8分钟)
2. 已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1.X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
易错点
点拨:(4分钟)
在使用根与系数的关系时,注意不要忽视前提条件
利用根与系数的关系,求一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2的
(1)平方和 :
(2)倒数和 :
(3)差的绝对值:
△=b2-4ac≥0
易错点:
课堂小结 (2分钟)
在方程ax2+bx+c=0(a≠0)中, a、b、c有哪些作用?
1、求根公式:
2、韦达定理:
1.下列方程的两根和与两根积各是多少?
2.已知两个数的和是1,积是-2,则这两个数是_______
3.若一个矩形的长和宽是一元二次方程 x -10x+20=0的
两根,则这个矩形的周长是_____ ,面积是_____
4.若方程2x -x=3的两根为 则
当堂训练(13分钟)
2和-1
20
20
5.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,求m+n的值.
解:∵关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,
∴-2+4=-m,-2×4=n,
解得m=-2,n=-8,
∴m+n=-10.
6. 方程 有一个正根,一个负根,求m的取值范围。
解:由已知可得:
△=
{
∴因此m的取值范围是 0
{
m>0
m-1<0
7. 方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
②∵两根互为倒数 m2 6m 5,
∴两根之积2m 1 1 ,∴ m 1且 0,
∴m 1时,方程的两根互为倒数.
③∵方程一根为0,
∴两根之积2m 1 0得 且 0,
∴ 时,方程有一根为零.
解: (m 1)2 4(2m 1) m2 6m 5
①∵两根互为相反数
∴两根之和m 1 0,m 1,且 0
∴m 1时,方程的两根互为相反数.
7. 方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
选做题
设x1,x2是方程x2-x-2 013=0的两实数根,则x13 +2 014x2-2 013= .
解 ∵x2-x-2 013=0,∴x2=x+2 013.
又∵x1,x2是方程x2-x-2 013=0的两实数根,
∴x1+x2=1,∴x13+2 014x2-2 013
=x1·x12+2 013x2+x2-2 013
=x1·(x1+2 013)+2 013x2+x2-2 013
=(x1+2 013)+2 013x1+2 013x2+x2-2 013
=x1+x2+2 013(x1+x2)+2 013-2 013
=1+2 013
=2 014.
答案 2 014
板书设计
2.5一元二次方程的根
与系数的关系
求根公式:
根与系数的关系:
公式推导:
设x1 、x2是一元二次方程ax2+bx+c=0 (a≠0)的两个根,
则x1=
X2=
负号千万别丢掉!
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
例:利用根与系数的关系,
求下列方程的两根之和、两根之积:
x2 +7x+6=0
解:这里a=1,b=7,c=6.
b2-4ac=7-4×1×6=49-24=25>0
∴方程有两个实数根。
∴x1+x2=-7,x1x2=6
为什么要加上这一步?
同课章节目录
