人教版七年级上册3.1 一元一次方程及其解法 (第3课时 )课件(共16张PPT)
文档属性
| 名称 | 人教版七年级上册3.1 一元一次方程及其解法 (第3课时 )课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:37:42 | ||
图片预览






文档简介
(共16张PPT)
3.1 一元一次方程及其解法
第3课时 去括号
去括号
学习目标
1. 会解含有括号的一元一次方程;
2. 知道解方程的过程就是化“复杂”为“简单”,化“未知”
为“已知”的过程,进一步体会化归思想;
3. 经历观察、思考、探索一元一次方程的解法的过程,进一步
提高学生分析问题和解决问题的能力;
4. 通过利用一元一次方程解决实际问题的过程,感受数学的应
用价值,激发学生的学习兴趣.
情境引入
我们一起来做一个游戏:
在心里默默的想一个数,先用这个数乘以2,再加上1,得到一个新的数,然后用这个新的数乘以5再减去1,说出最后的结果,我就能说出你心里想的那个数,你相信吗?
比如最后的结果是54,那么你心里想的那个数就是5.
你知道这是怎么算出来的吗?
设心里想的那个数是x,得
5(2x+1) 1=54
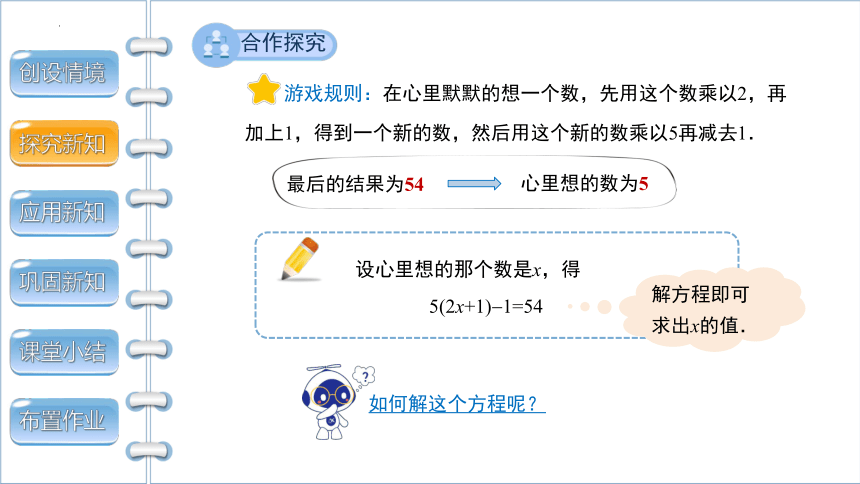
合作探究
游戏规则:在心里默默的想一个数,先用这个数乘以2,再加上1,得到一个新的数,然后用这个新的数乘以5再减去1.
解方程即可求出x的值.
如何解这个方程呢?
心里想的数为5
最后的结果为54
观察这个方程与我们上节课学习的方程有什么不同?
观察
含有括号
5(2x+1) 1=54
( )
上节课学习的解方程的步骤有哪些?
移项
合并同类型
系数化为1
上面的方程能直接进行移项吗?
不能,移项之前要先去括号.
还记得去括号法则吗?
如果括号前面是“ ”号,去括号时括号内的各项都不改变符号.
如果括号前面是“ ”号,去括号时括号内的各项都改变符号.
例:a+(b+c)=a+b+c
a–(b+c)=a–b–c
想一想
试着解下面的一元一次方程:
探究
5(2x+1) 1=54
10x+5 1=54
10x=54 5+1
10x=50
x=10
去括号
移项
合并同类项
系数化为1
当方程中含有括号时,要先去括号;
去括号的依据:去括号法则;
去括号时,不要漏乘括号内的项,同时注意符号.
将所得的结果54减去4再除以10即可得x的值.
注意
归纳
移项
合并同类型
系数化为1
去括号
解含括号的一元一次方程的步骤是什么?
注意符号
不要漏乘
移项变号
系数相加
注意符号
分子分母数的位置
去括号法则
依据
依据
等式性质1
乘法分配律
依据
等式性质2
依据
小组合作游戏:
两人一组,按照开头的游戏规则进行游戏,或者重新制定游戏规则.
合作
典型例题
分析
【例】解方程:2(x 2) 3(4x 1)=9(1 x).
移项
合并同类型
系数化为1
解此方程的步骤:
去括号
解:去括号,得
2x 4 12x+3=9 9x.
移项,得
2x 12x+9x=9+4 3.
合并同类项,得
x=10.
两边同除以 1,得
x= 10.
典型例题
【例】解方程:2(x 2) 3(4x 1)=9(1 x).
注意:①用分配律去括号时,不要漏乘括号中的项,并且不要搞错符号;
② x=10不是方程的解,必须把x系数化为1,才算完成解的过程.
随堂练习
1.解下列方程.
(1)
(2)
(1)
解:
去括号,得
移项,得
合并同类项,得
系数化为1,得
.
随堂练习
1.解下列方程.
(1)
(2)
(2)
解:
去括号,得
移项,得
合并同类项,得
系数化为1,得
去括号
解含括号的一元一次方程的步骤:
去括号的注意事项:
去括号时不要漏乘括号中的项,并且不要搞错符号;
去括号的依据:去括号法则.
移项
合并同类型
系数化为1
去括号
教科书
第89页 练习
第1、2题
再见
3.1 一元一次方程及其解法
第3课时 去括号
去括号
学习目标
1. 会解含有括号的一元一次方程;
2. 知道解方程的过程就是化“复杂”为“简单”,化“未知”
为“已知”的过程,进一步体会化归思想;
3. 经历观察、思考、探索一元一次方程的解法的过程,进一步
提高学生分析问题和解决问题的能力;
4. 通过利用一元一次方程解决实际问题的过程,感受数学的应
用价值,激发学生的学习兴趣.
情境引入
我们一起来做一个游戏:
在心里默默的想一个数,先用这个数乘以2,再加上1,得到一个新的数,然后用这个新的数乘以5再减去1,说出最后的结果,我就能说出你心里想的那个数,你相信吗?
比如最后的结果是54,那么你心里想的那个数就是5.
你知道这是怎么算出来的吗?
设心里想的那个数是x,得
5(2x+1) 1=54
合作探究
游戏规则:在心里默默的想一个数,先用这个数乘以2,再加上1,得到一个新的数,然后用这个新的数乘以5再减去1.
解方程即可求出x的值.
如何解这个方程呢?
心里想的数为5
最后的结果为54
观察这个方程与我们上节课学习的方程有什么不同?
观察
含有括号
5(2x+1) 1=54
( )
上节课学习的解方程的步骤有哪些?
移项
合并同类型
系数化为1
上面的方程能直接进行移项吗?
不能,移项之前要先去括号.
还记得去括号法则吗?
如果括号前面是“ ”号,去括号时括号内的各项都不改变符号.
如果括号前面是“ ”号,去括号时括号内的各项都改变符号.
例:a+(b+c)=a+b+c
a–(b+c)=a–b–c
想一想
试着解下面的一元一次方程:
探究
5(2x+1) 1=54
10x+5 1=54
10x=54 5+1
10x=50
x=10
去括号
移项
合并同类项
系数化为1
当方程中含有括号时,要先去括号;
去括号的依据:去括号法则;
去括号时,不要漏乘括号内的项,同时注意符号.
将所得的结果54减去4再除以10即可得x的值.
注意
归纳
移项
合并同类型
系数化为1
去括号
解含括号的一元一次方程的步骤是什么?
注意符号
不要漏乘
移项变号
系数相加
注意符号
分子分母数的位置
去括号法则
依据
依据
等式性质1
乘法分配律
依据
等式性质2
依据
小组合作游戏:
两人一组,按照开头的游戏规则进行游戏,或者重新制定游戏规则.
合作
典型例题
分析
【例】解方程:2(x 2) 3(4x 1)=9(1 x).
移项
合并同类型
系数化为1
解此方程的步骤:
去括号
解:去括号,得
2x 4 12x+3=9 9x.
移项,得
2x 12x+9x=9+4 3.
合并同类项,得
x=10.
两边同除以 1,得
x= 10.
典型例题
【例】解方程:2(x 2) 3(4x 1)=9(1 x).
注意:①用分配律去括号时,不要漏乘括号中的项,并且不要搞错符号;
② x=10不是方程的解,必须把x系数化为1,才算完成解的过程.
随堂练习
1.解下列方程.
(1)
(2)
(1)
解:
去括号,得
移项,得
合并同类项,得
系数化为1,得
.
随堂练习
1.解下列方程.
(1)
(2)
(2)
解:
去括号,得
移项,得
合并同类项,得
系数化为1,得
去括号
解含括号的一元一次方程的步骤:
去括号的注意事项:
去括号时不要漏乘括号中的项,并且不要搞错符号;
去括号的依据:去括号法则.
移项
合并同类型
系数化为1
去括号
教科书
第89页 练习
第1、2题
再见
