华师大版七年级下册8.2.2 不等式的简单变形 课件 (共20张PPT)
文档属性
| 名称 | 华师大版七年级下册8.2.2 不等式的简单变形 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 338.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 07:38:49 | ||
图片预览








文档简介
(共20张PPT)
不等式的
简单变形
1. 等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
2. 等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c(或a-c=b-c)
若a=b,则ac=bc(或 ,c≠0)
c
a
=
b
c
复习回顾
一、等式的基本性质
二、我们解一元一次方程有哪些基本步骤呢?
复习回顾
3、移项
4、合并同类项
5、系数化为1
1、去分母
2、去括号
移项要变号
如果把方程变为不等式我们该怎么解呢?不等式又有哪些性质?
例如解方程:
学习目标
1、理解并掌握不等式的性质
2、会正确运用不等式的性质解简单的不等式
3、体会类比与转化的思想
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
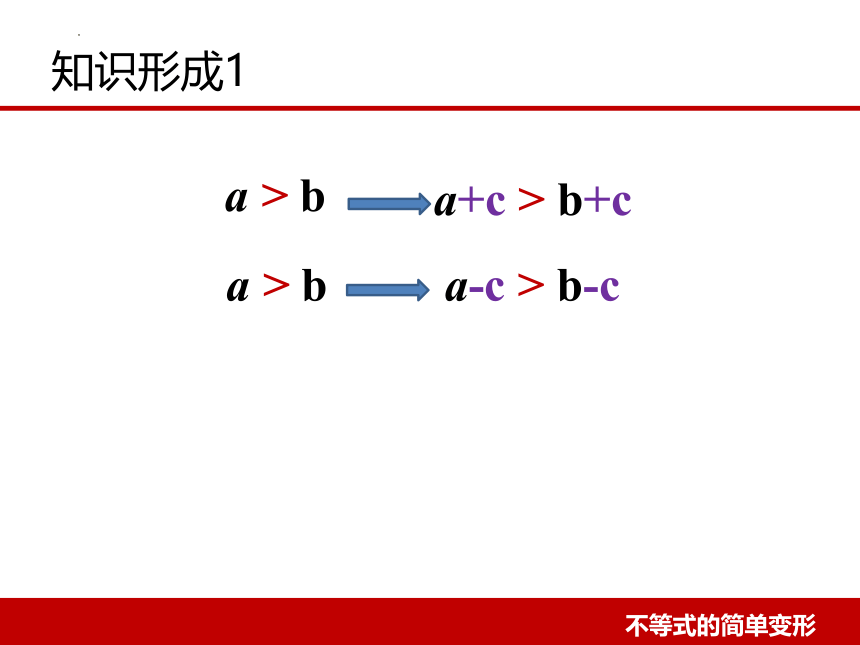
知识形成1
a > b
a+c > b+c
a-c > b-c
a > b
知识形成1
性质1、不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.
如果 a > b , 那么 a+c > b+c , a-c > b-c
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
知识形成2
试一试:根据不等式 7>4,用“>”“<”填空 并观察不等号的方向是否发生改变:
(1) 7× 3___4 ×3 (5) 7×(-1)___4×(-1)
(2) 7× 2 __4 ×2 (6) 7×(-2)___4×(-2)
(3) 7× 1___4 ×1 (7) 7×(-3)___4×(-3)
(4) 7× 0___4 ×0
>
>
>
=
<
<
<
不变
不变
不变
改变
改变
改变
知识形成2
性质2、不等式的两边都乘以(或除以)同一个
正数,不等号的方向不变.
如果 a > b,并且c>0, 那么ac>bc,
>
c
a
c
b
如果a>b,并且c<0, 那么ac<
c
a
c
b
性质3、不等式的两边都乘以(或除以)同一个
负数,不等号的方向改变.
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
例1 解不等式:
解:
(1)不等式的两边都加上7,不等式的方向不变,
x-7+7<8+7,
得 x<15
(2)不等式的两边都减去2x(即加上-2x),不等号的方向不变,
3x-2x<2x-3-2x
得 x<-3
这里的变形,与方程变形中的移项相类似,它依据的是不等式的性质1注意:移项要改变符号
(1)x-7<8 (2)3x<2x-3
所以
所以
这两小题中不等式的变形与方程的什么变形类似
x<8+7
3x-2x<-3
例2 解不等式:
解:
(1)不等式的两边都乘以2,不等号的方向不变,
1
2
x×2>(-3)×2
得 x>-6
(2)不等式的两边都除以-2(即乘以- ),不等号的方向改变,
1
2
得 x>-3
1
2
(1) x>-3 (2)-2x<6
所以
所以
-2x×(- )>6×(- )
1
2
1
2
这里的变形,与方程变形中的“将未知数的系数化为1”相类似,它依据的是不等式的性质2或3,要注意不等式两边乘以(或除以)的数是正数还是负数,确定变形时不等号的方向是否需要改变。
这两小题中不等式的变形与方程的什么变形类似 有什么不同
小试牛刀
1、判断对错并说明理由
(1) 因为-3<0,所以-3+1<1 ( )
(2) 因为-3 × 2> -5 ×2,所以-3<-5 ( )
(7)因为-2<1,所以-2a < a ( )
(3)若a(4)若-6a<-6 b,则a(5)若a>b,则-a<-b ( )
(6)若-2x>0,则x>0 ( )
(8)若a>0,则3a>2a ( )
√
√
√
√
×
×
×
×
小试牛刀
1、 根据不等式的基本性质,把下列不等式化成
x>a或x(1) x-2<3 (2) 6x<5x-1 (3) x>5 (4) –4x>3
(1)解:x-2+2<3+2
x<5
(2)解:6x-5x<5x-1-5x
x<-1
(3)解: x×3>5×3
x>15
(4)解: –4x× <3×
x<
1
3
1
3
(- )
1
4
(- )
1
4
-
3
4
大显身手
1. 设a>b,用“<”或“>”填空.
(1)- 4a____ - 4b
(2) 2-4a______2-4b
<
<
2.若-m>5,则m _____ - 5.
<
3. 由xmy的条件是 ( )
A . m≥0 B . m≤0 C. m>0 D. m<0
4.若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定
D
D
5.不等式17-3x>2的正整数解的个数是( )
A. 2
B. 3
C.4
D. 5
C
大显身手
变式训练
解下列不等式,并在数轴上表示出来:
1. x-2>0 2. x+1>0
3. -2x<4 4. 3x≤0
我们的收获
1、掌握不等式的性质
2、会正确运用不等式的性质解简单的不等式
(注意问题:不等式的基本性质3)
3、分清不等式、等式性质的异同点体会类比与转化的思想
不等式的
简单变形
1. 等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
2. 等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c(或a-c=b-c)
若a=b,则ac=bc(或 ,c≠0)
c
a
=
b
c
复习回顾
一、等式的基本性质
二、我们解一元一次方程有哪些基本步骤呢?
复习回顾
3、移项
4、合并同类项
5、系数化为1
1、去分母
2、去括号
移项要变号
如果把方程变为不等式我们该怎么解呢?不等式又有哪些性质?
例如解方程:
学习目标
1、理解并掌握不等式的性质
2、会正确运用不等式的性质解简单的不等式
3、体会类比与转化的思想
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
知识形成1
a > b
a+c > b+c
a-c > b-c
a > b
知识形成1
性质1、不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.
如果 a > b , 那么 a+c > b+c , a-c > b-c
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
知识形成2
试一试:根据不等式 7>4,用“>”“<”填空 并观察不等号的方向是否发生改变:
(1) 7× 3___4 ×3 (5) 7×(-1)___4×(-1)
(2) 7× 2 __4 ×2 (6) 7×(-2)___4×(-2)
(3) 7× 1___4 ×1 (7) 7×(-3)___4×(-3)
(4) 7× 0___4 ×0
>
>
>
=
<
<
<
不变
不变
不变
改变
改变
改变
知识形成2
性质2、不等式的两边都乘以(或除以)同一个
正数,不等号的方向不变.
如果 a > b,并且c>0, 那么ac>bc,
>
c
a
c
b
如果a>b,并且c<0, 那么ac
c
a
c
b
性质3、不等式的两边都乘以(或除以)同一个
负数,不等号的方向改变.
自主学习
用约5分钟自学课本55—57页,完成下列问题
1、自学课本55页,理解掌握不等式的性质1
2、自学课本56页,理解掌握不等式的性质2、性质3
3、自学课本57页
自学 例1,总结怎样进行不等式的“移项”;
自学 例2,总结怎样进行不等式的“系数化1”
例1 解不等式:
解:
(1)不等式的两边都加上7,不等式的方向不变,
x-7+7<8+7,
得 x<15
(2)不等式的两边都减去2x(即加上-2x),不等号的方向不变,
3x-2x<2x-3-2x
得 x<-3
这里的变形,与方程变形中的移项相类似,它依据的是不等式的性质1注意:移项要改变符号
(1)x-7<8 (2)3x<2x-3
所以
所以
这两小题中不等式的变形与方程的什么变形类似
x<8+7
3x-2x<-3
例2 解不等式:
解:
(1)不等式的两边都乘以2,不等号的方向不变,
1
2
x×2>(-3)×2
得 x>-6
(2)不等式的两边都除以-2(即乘以- ),不等号的方向改变,
1
2
得 x>-3
1
2
(1) x>-3 (2)-2x<6
所以
所以
-2x×(- )>6×(- )
1
2
1
2
这里的变形,与方程变形中的“将未知数的系数化为1”相类似,它依据的是不等式的性质2或3,要注意不等式两边乘以(或除以)的数是正数还是负数,确定变形时不等号的方向是否需要改变。
这两小题中不等式的变形与方程的什么变形类似 有什么不同
小试牛刀
1、判断对错并说明理由
(1) 因为-3<0,所以-3+1<1 ( )
(2) 因为-3 × 2> -5 ×2,所以-3<-5 ( )
(7)因为-2<1,所以-2a < a ( )
(3)若a
(6)若-2x>0,则x>0 ( )
(8)若a>0,则3a>2a ( )
√
√
√
√
×
×
×
×
小试牛刀
1、 根据不等式的基本性质,把下列不等式化成
x>a或x
(1)解:x-2+2<3+2
x<5
(2)解:6x-5x<5x-1-5x
x<-1
(3)解: x×3>5×3
x>15
(4)解: –4x× <3×
x<
1
3
1
3
(- )
1
4
(- )
1
4
-
3
4
大显身手
1. 设a>b,用“<”或“>”填空.
(1)- 4a____ - 4b
(2) 2-4a______2-4b
<
<
2.若-m>5,则m _____ - 5.
<
3. 由x
A . m≥0 B . m≤0 C. m>0 D. m<0
4.若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定
D
D
5.不等式17-3x>2的正整数解的个数是( )
A. 2
B. 3
C.4
D. 5
C
大显身手
变式训练
解下列不等式,并在数轴上表示出来:
1. x-2>0 2. x+1>0
3. -2x<4 4. 3x≤0
我们的收获
1、掌握不等式的性质
2、会正确运用不等式的性质解简单的不等式
(注意问题:不等式的基本性质3)
3、分清不等式、等式性质的异同点体会类比与转化的思想
