人教版数学七年级上册 2.2 整式的加减(3)课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级上册 2.2 整式的加减(3)课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 08:48:40 | ||
图片预览





文档简介
(共17张PPT)
2.2 整式的加减
第3课时
1.合并同类项的法则是:
合并同类项后,所得项的系数是 ,
且 不变.
2.去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的
符号与原来的符号 ;如果括号外的因数是负数,去括
号后 .
合并前各同类项的系数的和
字母连同它的指数
相同
原括号内各项的符号与原来的符号相反
1.掌握整式加减运算的法则,会进行整式加减运算,提高运算能力.
2.能根据题意列出式子,提高综合运用知识进行分析、解决问题的能力,体会整式的应用价值.
整式加减的一般步骤:
简单地讲就是:先去括号,再合并同类项.
注意:整式加减运算的结果仍然是整式.
(1)如果有括号,那么先去括号.
(2)观察有无同类项.
(3)利用加法的交换律和结合律,分组同类项.
(4)合并同类项.
例1 计算:
(1)(2x-3y)+(5x+4y)
(2)(8a-7b)-(4a-5b)
=2x-3y+5x+4y
=4a-2b
=7x+y
=8a-7b-4a+5b
【例题】
【例2】做大小两个长方形纸盒,尺寸如下(单位:cm)
(1)做这两个纸盒共用料多少cm2?
(2)做大纸盒比做小纸盒多用料多少cm2?
长 宽 高
小纸盒 a b c
大纸盒 2 a 3 b 4 c
【例题】
解:小纸盒的表面积是:
大纸盒的表面积是:
(1)做这两个纸盒共用料:
(2)做大纸盒比做小纸盒多用料:
1.某中学合唱团出场时第一排站了n名同学,从第二排起每一排都比前面一排多1人,一共站了四排,则该合唱团一共有多少名同学参加?
解:由已知得,从第二排起,到第四排,人数分别为:
(n+1)人,(n+2)人,(n+3)人.
所以 该合唱团总共有:n+(n+1)+(n+2)+(n+3)
=(4n+6)人
答:该合唱团一共有(4n+6)名同学参加.
【跟踪训练】
2.代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a,b的值.
解:(x2+ax-2y+7)-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1=(1-b)x2+(a+2)x-11y+8
因为代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字 母x的取值无关,
所以1-b=0,a+2=0,解得a=-2 ,b=1.
答:a=-2 ,b=1.
去括号
2.整式加减的结果是________或________.
单项式
多项式
1.整式加减的运算法则:一般地,几个整式相加减,如果有括号就_________ ,然后________________.
再合并同类项
1.计算3x2-2x+1-(3+x+3x2).
解:原式=3x2-2x+1-3-x-3x2
=3x2-3x2-2x-x+1-3=-3x-2.
2.计算(3a2+2a+1)-(2a2+3a-5)的结果是( )
A.a2-5a+6 B.a2-5a-4 C.a2-a-4 D.a2-a+6
D
3.求下列式子的值:
(1)a+2 -3(a-b),其中a=-3,b=2;
(2)5ab2-{2a2b-[3ab2-(4ab2-2a2b)]},
其中a=-3,b=0.5.
【答案】化简得2a,值为-6
【答案】 化简得:4ab2,值为-3
4.若代数式(2x2+ax-5y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-ab-b2)-(4a2+ab+b2)的值.
【解析】(2x2+ax-5y+b)-(2bx2-3x+5y-1)= 2x2+ax-5y+b-2bx2+3x-5y+1=(2-2b)x2+(a+3)x+(-5-5)y+b+1,
因为式子的值与字母x的取值无关,所以2-2b=0,a+3=0,
所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)= 3a2-3ab-3b2-4a2-ab-b2=
-a2-4ab-4b2=-(-3)2-4×(-3)×1-4×12 =-1.
5.为资助贫困山区儿童入学,我校甲、乙、丙三位同学
决定把平时节省下来的零花钱捐给希望工程,已知甲同
学捐资x元,乙同学捐资比甲同学捐资的3倍少8元,丙同
学捐资数是甲和乙同学捐资数的总和的 ,求甲、乙、
丙三位同学的捐资总数.
解:根据题意设,甲同学捐资x元,乙同学捐资(3x-8)元,
那么,丙同学捐资 [x+(3x-8)]元.
则甲、乙、丙的捐资总数为:
x+(3x-8)+ [x+(3x-8)]
=x+3x-8+ (4x-8)=x+3x-8+3x-6=7x-14,
答:甲、乙、丙的捐资总数为(7x-14)元.
奋斗,是理想与毅力合成的混凝土,它能架成通向彼岸的桥梁.
2.2 整式的加减
第3课时
1.合并同类项的法则是:
合并同类项后,所得项的系数是 ,
且 不变.
2.去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的
符号与原来的符号 ;如果括号外的因数是负数,去括
号后 .
合并前各同类项的系数的和
字母连同它的指数
相同
原括号内各项的符号与原来的符号相反
1.掌握整式加减运算的法则,会进行整式加减运算,提高运算能力.
2.能根据题意列出式子,提高综合运用知识进行分析、解决问题的能力,体会整式的应用价值.
整式加减的一般步骤:
简单地讲就是:先去括号,再合并同类项.
注意:整式加减运算的结果仍然是整式.
(1)如果有括号,那么先去括号.
(2)观察有无同类项.
(3)利用加法的交换律和结合律,分组同类项.
(4)合并同类项.
例1 计算:
(1)(2x-3y)+(5x+4y)
(2)(8a-7b)-(4a-5b)
=2x-3y+5x+4y
=4a-2b
=7x+y
=8a-7b-4a+5b
【例题】
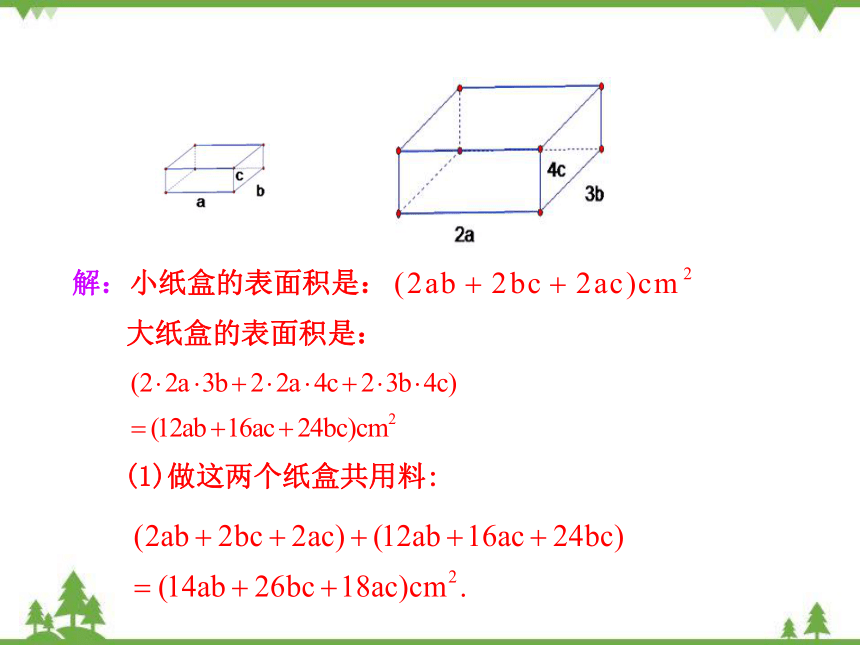
【例2】做大小两个长方形纸盒,尺寸如下(单位:cm)
(1)做这两个纸盒共用料多少cm2?
(2)做大纸盒比做小纸盒多用料多少cm2?
长 宽 高
小纸盒 a b c
大纸盒 2 a 3 b 4 c
【例题】
解:小纸盒的表面积是:
大纸盒的表面积是:
(1)做这两个纸盒共用料:
(2)做大纸盒比做小纸盒多用料:
1.某中学合唱团出场时第一排站了n名同学,从第二排起每一排都比前面一排多1人,一共站了四排,则该合唱团一共有多少名同学参加?
解:由已知得,从第二排起,到第四排,人数分别为:
(n+1)人,(n+2)人,(n+3)人.
所以 该合唱团总共有:n+(n+1)+(n+2)+(n+3)
=(4n+6)人
答:该合唱团一共有(4n+6)名同学参加.
【跟踪训练】
2.代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a,b的值.
解:(x2+ax-2y+7)-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1=(1-b)x2+(a+2)x-11y+8
因为代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字 母x的取值无关,
所以1-b=0,a+2=0,解得a=-2 ,b=1.
答:a=-2 ,b=1.
去括号
2.整式加减的结果是________或________.
单项式
多项式
1.整式加减的运算法则:一般地,几个整式相加减,如果有括号就_________ ,然后________________.
再合并同类项
1.计算3x2-2x+1-(3+x+3x2).
解:原式=3x2-2x+1-3-x-3x2
=3x2-3x2-2x-x+1-3=-3x-2.
2.计算(3a2+2a+1)-(2a2+3a-5)的结果是( )
A.a2-5a+6 B.a2-5a-4 C.a2-a-4 D.a2-a+6
D
3.求下列式子的值:
(1)a+2 -3(a-b),其中a=-3,b=2;
(2)5ab2-{2a2b-[3ab2-(4ab2-2a2b)]},
其中a=-3,b=0.5.
【答案】化简得2a,值为-6
【答案】 化简得:4ab2,值为-3
4.若代数式(2x2+ax-5y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-ab-b2)-(4a2+ab+b2)的值.
【解析】(2x2+ax-5y+b)-(2bx2-3x+5y-1)= 2x2+ax-5y+b-2bx2+3x-5y+1=(2-2b)x2+(a+3)x+(-5-5)y+b+1,
因为式子的值与字母x的取值无关,所以2-2b=0,a+3=0,
所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)= 3a2-3ab-3b2-4a2-ab-b2=
-a2-4ab-4b2=-(-3)2-4×(-3)×1-4×12 =-1.
5.为资助贫困山区儿童入学,我校甲、乙、丙三位同学
决定把平时节省下来的零花钱捐给希望工程,已知甲同
学捐资x元,乙同学捐资比甲同学捐资的3倍少8元,丙同
学捐资数是甲和乙同学捐资数的总和的 ,求甲、乙、
丙三位同学的捐资总数.
解:根据题意设,甲同学捐资x元,乙同学捐资(3x-8)元,
那么,丙同学捐资 [x+(3x-8)]元.
则甲、乙、丙的捐资总数为:
x+(3x-8)+ [x+(3x-8)]
=x+3x-8+ (4x-8)=x+3x-8+3x-6=7x-14,
答:甲、乙、丙的捐资总数为(7x-14)元.
奋斗,是理想与毅力合成的混凝土,它能架成通向彼岸的桥梁.
