上海市上海大学嘉定附高2022-2023学年高二上学期9月开学考试数学试题(含答案)
文档属性
| 名称 | 上海市上海大学嘉定附高2022-2023学年高二上学期9月开学考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 00:00:00 | ||
图片预览


文档简介
上海大学嘉定附高2022-2023学年高二上学期9月开学考试数学试题
一 填空题(本大题满分40分,本大题共有10题)
1. 在空间中,如果两条直线没有交点,那么这两条直线的位置关系是___________.
2. 已知正△ABC边长为a,那么△ABC的平面直观图的面积为______.
3. 若正四棱柱的底面边长为2,高为4,则异面直线与 所成角的余弦值是_________.
4. 正方体中,棱长为分别是、的中点,是底面的中心,过作截面,则所得截面的面积为___________.
5. 若圆柱侧面展开图是一个正方形,则它的母线长和底面半径的比值是__________.
6. 在正方体中,是的中点,则直线与平面所成的角大小为___________(结果用反三角函数表示).
7. 有下列四个命题:①三点可以确定一个平面:②若一条直线垂直于平面内的无数条直线,则该直线与平面垂直;③垂直于同一平面的两条直线平行;④若直线a,b与直线c相交成等角,则.其中正确命题的序号是___________.
8. 如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是 ____ cm3.
9. 直线交平面于点,与所成角为上两点到平面的距离分别为2 4,则长为___________.
10. 如图,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是下图中的_______________. (要求:把可能的图的序号都填上)
二 选择题(本大题满分16分,本大题共有4题)
11. 若a,b是异面直线,直线,则c与b位置关系是( )
A. 相交 B. 异面 C. 平行 D. 异面或相交
12. 三个互不重合的平面把空间分成六个部分时,它们的交线有( )
A. 1条 B. 2条 C. 3条 D. 1条或2条
13. 已知为两条不同的直线,为两个不同的平面,给出下列4个命题:
①若,则 ②若,则.
③若,. ④若,则.
其中真命题的序号为
A. ①② B. ①④ C. ③④ D. ②③
14. 二面角是直二面角,,,设直线与、所成的角分别为和,则( )
A. B.
C. D.
三 解答题(本大题满分64分,本大题共有5题)
15. 如图,和是异面直线,分别为线段上的点,且,求和所成角的大小.
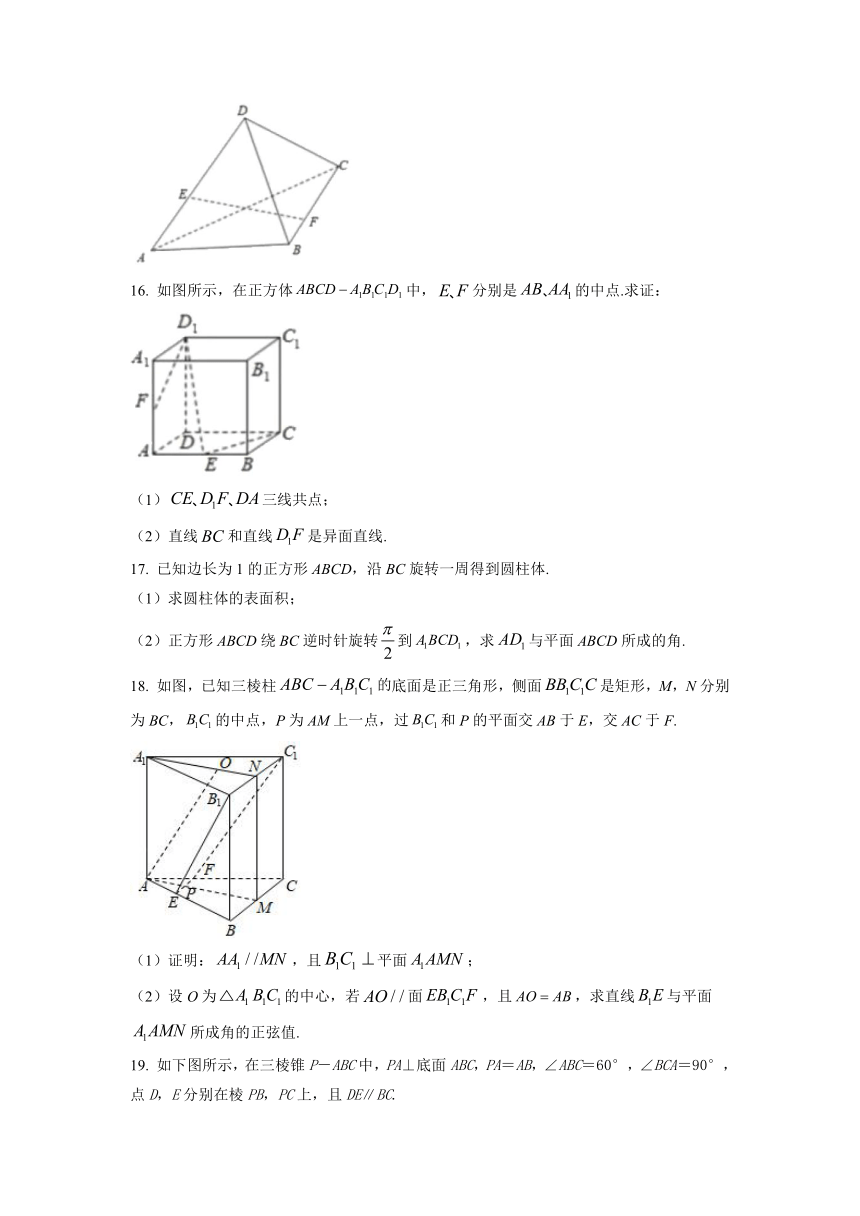
16. 如图所示,在正方体中,分别是的中点.求证:
(1)三线共点;
(2)直线和直线是异面直线.
17. 已知边长为1的正方形ABCD,沿BC旋转一周得到圆柱体.
(1)求圆柱体的表面积;
(2)正方形ABCD绕BC逆时针旋转到,求与平面ABCD所成的角.
18. 如图,已知三棱柱底面是正三角形,侧面是矩形,M,N分别为BC,的中点,P为AM上一点,过和P的平面交AB于E,交AC于F.
(1)证明:,且平面;
(2)设O为的中心,若面,且,求直线与平面所成角的正弦值.
19. 如下图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.
上海大学嘉定附高2022-2023学年高二上学期9月开学考试
数学试题答案
一 填空题(本大题满分40分,本大题共有10题)
【1题答案】
【答案】平行或异面
【2题答案】
【答案】##
【3题答案】
【答案】
【4题答案】
【答案】##
【5题答案】
【答案】
【6题答案】
【答案】##
【7题答案】
【答案】③
【8题答案】
【答案】
【9题答案】
【答案】或
【10题答案】
【答案】②③
二 选择题(本大题满分16分,本大题共有4题)
【11题答案】
【答案】D
【12题答案】
【答案】D
【13题答案】
【答案】D
【14题答案】
【答案】C
三 解答题(本大题满分64分,本大题共有5题)
【15题答案】
【答案】
【16题答案】
【答案】(1)略 (2)略
【17题答案】
【答案】(1)4π;(2)
【18题答案】
【答案】(1)答案略;(2)
【19题答案】
【答案】(1)证明略;(2) (3)略
一 填空题(本大题满分40分,本大题共有10题)
1. 在空间中,如果两条直线没有交点,那么这两条直线的位置关系是___________.
2. 已知正△ABC边长为a,那么△ABC的平面直观图的面积为______.
3. 若正四棱柱的底面边长为2,高为4,则异面直线与 所成角的余弦值是_________.
4. 正方体中,棱长为分别是、的中点,是底面的中心,过作截面,则所得截面的面积为___________.
5. 若圆柱侧面展开图是一个正方形,则它的母线长和底面半径的比值是__________.
6. 在正方体中,是的中点,则直线与平面所成的角大小为___________(结果用反三角函数表示).
7. 有下列四个命题:①三点可以确定一个平面:②若一条直线垂直于平面内的无数条直线,则该直线与平面垂直;③垂直于同一平面的两条直线平行;④若直线a,b与直线c相交成等角,则.其中正确命题的序号是___________.
8. 如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是 ____ cm3.
9. 直线交平面于点,与所成角为上两点到平面的距离分别为2 4,则长为___________.
10. 如图,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是下图中的_______________. (要求:把可能的图的序号都填上)
二 选择题(本大题满分16分,本大题共有4题)
11. 若a,b是异面直线,直线,则c与b位置关系是( )
A. 相交 B. 异面 C. 平行 D. 异面或相交
12. 三个互不重合的平面把空间分成六个部分时,它们的交线有( )
A. 1条 B. 2条 C. 3条 D. 1条或2条
13. 已知为两条不同的直线,为两个不同的平面,给出下列4个命题:
①若,则 ②若,则.
③若,. ④若,则.
其中真命题的序号为
A. ①② B. ①④ C. ③④ D. ②③
14. 二面角是直二面角,,,设直线与、所成的角分别为和,则( )
A. B.
C. D.
三 解答题(本大题满分64分,本大题共有5题)
15. 如图,和是异面直线,分别为线段上的点,且,求和所成角的大小.
16. 如图所示,在正方体中,分别是的中点.求证:
(1)三线共点;
(2)直线和直线是异面直线.
17. 已知边长为1的正方形ABCD,沿BC旋转一周得到圆柱体.
(1)求圆柱体的表面积;
(2)正方形ABCD绕BC逆时针旋转到,求与平面ABCD所成的角.
18. 如图,已知三棱柱底面是正三角形,侧面是矩形,M,N分别为BC,的中点,P为AM上一点,过和P的平面交AB于E,交AC于F.
(1)证明:,且平面;
(2)设O为的中心,若面,且,求直线与平面所成角的正弦值.
19. 如下图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.
上海大学嘉定附高2022-2023学年高二上学期9月开学考试
数学试题答案
一 填空题(本大题满分40分,本大题共有10题)
【1题答案】
【答案】平行或异面
【2题答案】
【答案】##
【3题答案】
【答案】
【4题答案】
【答案】##
【5题答案】
【答案】
【6题答案】
【答案】##
【7题答案】
【答案】③
【8题答案】
【答案】
【9题答案】
【答案】或
【10题答案】
【答案】②③
二 选择题(本大题满分16分,本大题共有4题)
【11题答案】
【答案】D
【12题答案】
【答案】D
【13题答案】
【答案】D
【14题答案】
【答案】C
三 解答题(本大题满分64分,本大题共有5题)
【15题答案】
【答案】
【16题答案】
【答案】(1)略 (2)略
【17题答案】
【答案】(1)4π;(2)
【18题答案】
【答案】(1)答案略;(2)
【19题答案】
【答案】(1)证明略;(2) (3)略
同课章节目录
