沪科版数学九年级下册 第25章 投影与视图 达标测试卷2022-2023学年(含答案)
文档属性
| 名称 | 沪科版数学九年级下册 第25章 投影与视图 达标测试卷2022-2023学年(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 09:48:13 | ||
图片预览



文档简介
第25章 投影与视图 达标测试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称为“阳马”(如图).“阳马”的俯视图是( )
(第1题) (第3题)
2.木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m
C.等于1.2 m D.小于或等于1.2 m
3.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.可能为太阳光线或灯光光线 D.该影子实际不可能存在
4.小亮在某天的8时、9时30分、10时、12时四次到室外的阳光下观察向日葵随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.12时 B.10时
C.9时30分 D.8时
5.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
(第5题) (第6题)
6.如图是由一个正方体在底部截去了一个半圆柱得到的几何体,则其左视图是( )
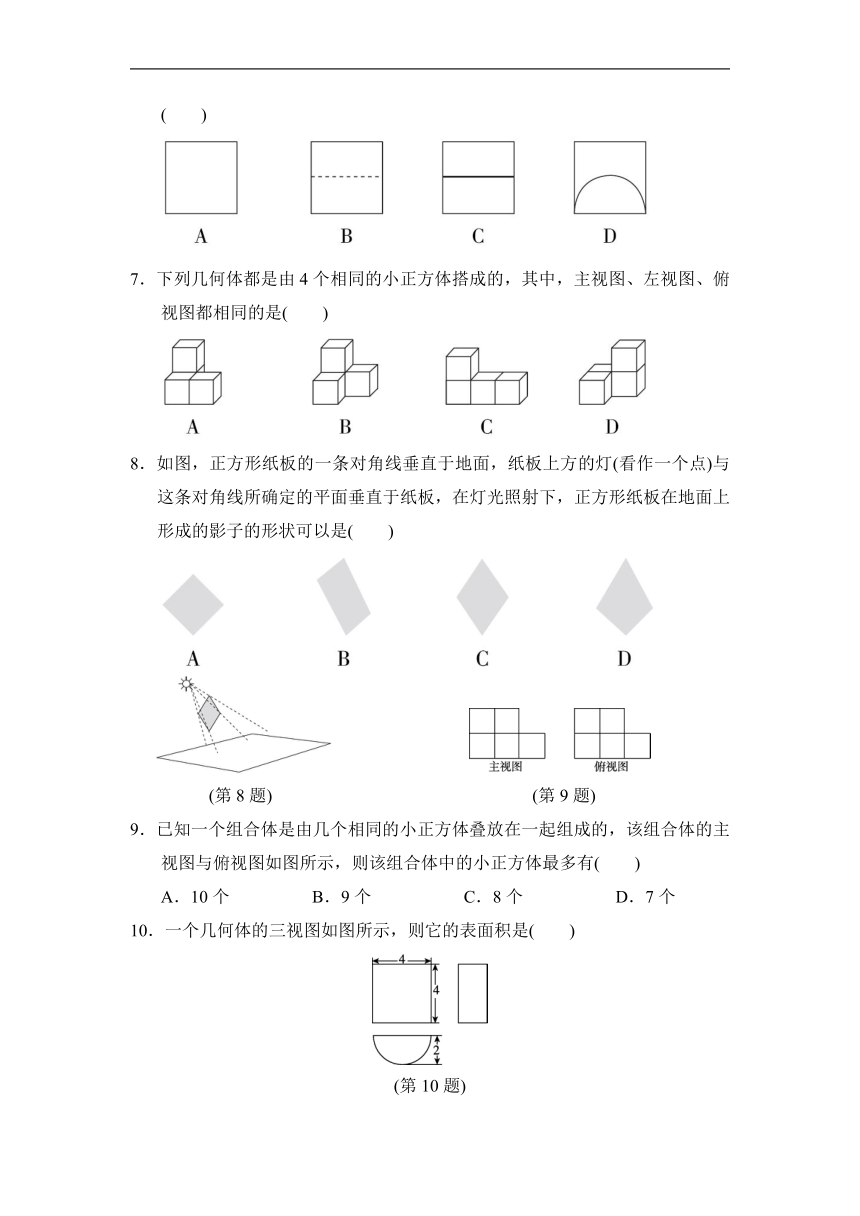
7.下列几何体都是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )
8.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
(第8题) (第9题)
9.已知一个组合体是由几个相同的小正方体叠放在一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中的小正方体最多有( )
A.10个 B.9个 C.8个 D.7个
10.一个几何体的三视图如图所示,则它的表面积是( )
(第10题)
A.24+2π B.16+4π
C.16+8π D.16+12π
二、填空题(本大题共4小题,每小题5分,共20分)
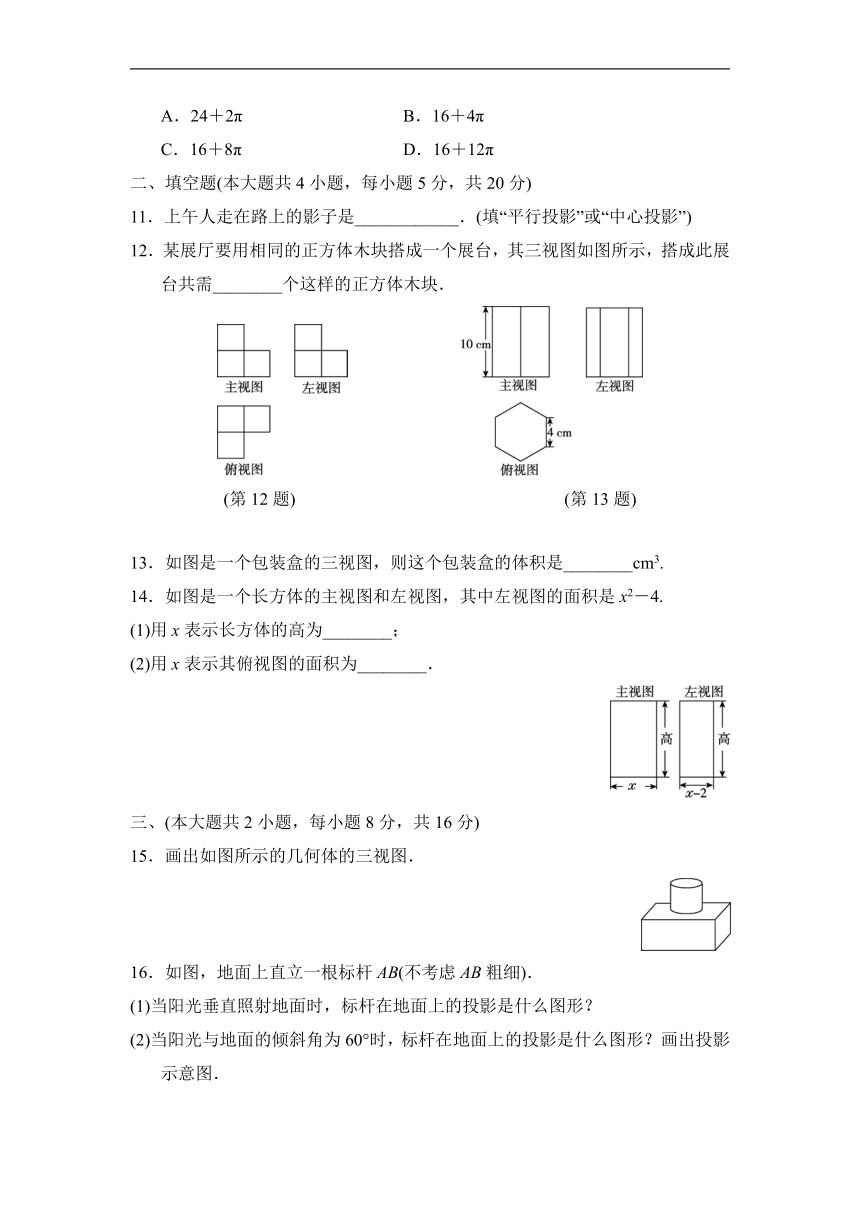
11.上午人走在路上的影子是____________.(填“平行投影”或“中心投影”)
12.某展厅要用相同的正方体木块搭成一个展台,其三视图如图所示,搭成此展台共需________个这样的正方体木块.
(第12题) (第13题)
13.如图是一个包装盒的三视图,则这个包装盒的体积是________cm3.
14.如图是一个长方体的主视图和左视图,其中左视图的面积是x2-4.
(1)用x表示长方体的高为________;
(2)用x表示其俯视图的面积为________.
三、(本大题共2小题,每小题8分,共16分)
15.画出如图所示的几何体的三视图.
16.如图,地面上直立一根标杆AB(不考虑AB粗细).
(1)当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?画出投影示意图.
四、(本大题共2小题,每小题8分,共16分)
17.一个圆锥的主视图与左视图都是边长为2 cm的等边三角形,求其俯视图的面积.
18.在长、宽都为4 m,高为3 m的房间的正中央的天花板上悬挂一只白炽灯泡,为了集中光线,加上了灯罩,如图,已知灯罩深8 cm,灯泡离地面2 m,为了使光线恰好照在墙脚,问灯罩的直径应为多少?
五、(本大题共2小题,每小题10分,共20分)
19.一个几何体是由棱长为1的小立方体搭建而成的,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方体的个数.
(1)画出该几何体的主视图和左视图;
(2)求该几何体的体积和表面积.
20.如图,电线杆上有一盏路灯,电线杆与三个等高的标杆整齐地排列在笔直的马路一侧,AB,CD,EF是三个标杆,相邻的两个标杆之间的距离都是2 m,已知AB,CD在灯光下的影长分别为BM=1.6 m,DN=0.6 m.
(1)请画出路灯的位置和标杆EF在路灯灯光下的影子;
(2)求标杆EF的影长.
六、(本题满分12分)
21.如图,用10个大小相同的小正方体搭成一个组合体.
(1)请在指定位置画出该组合体的左视图、俯视图;
(2)在不改变该组合体中小正方体个数的前提下,从中移动一个小正方体,使所得新组合体与原组合体相比,左视图、俯视图形状保持不变,但主视图的形状改变,请画出新组合体主视图的所有可能的形状.(所给的方格图不一定全用,不够可添)
七、(本题满分12分)
22.如图是由两个长方体组合而成的一个几何体的三视图,根据图中所标尺寸(单位:mm),计算这个几何体的表面积.
八、(本题满分14分)
23.一透明的敞口正方体容器ABCD A′B′C′D′中装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α).
探究:如图①,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②所示.解决问题:
(1)CQ与BE的位置关系是________,BQ的长是________dm;
(2)求液体的体积;[参考算法:直三棱柱体积(V液)=底面积(S△BCQ)×高(AB)]
(3)求液面到桌面的高度和倾斜角α的度数.(注:sin 37°≈,tan 37°≈)
答案
一、1.A 2.D 3.B 4.D 5.B 6.B 7.A 8.D 9.B 10.D
二、11.平行投影 12.4 13.240
14.(1)x+2 (2)x2-2x
三、15.解:如图所示.
16.解:(1)当阳光垂直照射地面时,标杆在地面上的投影是一个点.
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是线段BC,如图所示.
四、17.解:由题意得圆锥的底面圆的半径为1 cm,
∴π×12=π(cm2).
∴其俯视图的面积为π cm2.
18.解:过点A作AM⊥DE于点M,交BC于点N,则AN⊥BC.
由题意得BC∥DE,
∴△ABC∽△ADE.
∴=,
即=.
∴BC=0.16 m=16 cm,
即灯罩的直径为16 cm.
五、19.解:(1)如图所示.
(2)体积:1×1×1×(2+2+3+1)=8.
表面积:1×1×(6×2+4×2+5×2)=30.
20.解:(1)如图所示,O处为路灯的位置,标杆EF在路灯灯光下的影子为FP.
(2)如图,连接AE,由题意可知点C在AE上.设FP的长度为x m,易知=,=,
∴=,
即=,
解得x=0.4.
经检验,x=0.4是方程的解且符合题意,
∴标杆EF的影长为0.4 m.
六、21.解:(1)如图①所示.
(2)如图②所示.
七、22.解:S表=(6×8+6×2+2×8+4×4+4×2)×2=200(mm2),即这个几何体的表面积为200 mm2.
八、23.解:(1)平行;3
(2)V液=×3×4×4=24(dm3).
(3)过点B作BF⊥CQ,垂足为F.
∵×3×4=×5×BF,
∴BF= dm.
∴液面到桌面的高度是 dm.
在Rt△BCQ中,∵tan ∠BCQ=,
∴α=∠BCQ≈37°.
一、选择题(本大题共10小题,每小题4分,共40分)
1.在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称为“阳马”(如图).“阳马”的俯视图是( )
(第1题) (第3题)
2.木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m
C.等于1.2 m D.小于或等于1.2 m
3.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.可能为太阳光线或灯光光线 D.该影子实际不可能存在
4.小亮在某天的8时、9时30分、10时、12时四次到室外的阳光下观察向日葵随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.12时 B.10时
C.9时30分 D.8时
5.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
(第5题) (第6题)
6.如图是由一个正方体在底部截去了一个半圆柱得到的几何体,则其左视图是( )
7.下列几何体都是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )
8.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
(第8题) (第9题)
9.已知一个组合体是由几个相同的小正方体叠放在一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中的小正方体最多有( )
A.10个 B.9个 C.8个 D.7个
10.一个几何体的三视图如图所示,则它的表面积是( )
(第10题)
A.24+2π B.16+4π
C.16+8π D.16+12π
二、填空题(本大题共4小题,每小题5分,共20分)
11.上午人走在路上的影子是____________.(填“平行投影”或“中心投影”)
12.某展厅要用相同的正方体木块搭成一个展台,其三视图如图所示,搭成此展台共需________个这样的正方体木块.
(第12题) (第13题)
13.如图是一个包装盒的三视图,则这个包装盒的体积是________cm3.
14.如图是一个长方体的主视图和左视图,其中左视图的面积是x2-4.
(1)用x表示长方体的高为________;
(2)用x表示其俯视图的面积为________.
三、(本大题共2小题,每小题8分,共16分)
15.画出如图所示的几何体的三视图.
16.如图,地面上直立一根标杆AB(不考虑AB粗细).
(1)当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?画出投影示意图.
四、(本大题共2小题,每小题8分,共16分)
17.一个圆锥的主视图与左视图都是边长为2 cm的等边三角形,求其俯视图的面积.
18.在长、宽都为4 m,高为3 m的房间的正中央的天花板上悬挂一只白炽灯泡,为了集中光线,加上了灯罩,如图,已知灯罩深8 cm,灯泡离地面2 m,为了使光线恰好照在墙脚,问灯罩的直径应为多少?
五、(本大题共2小题,每小题10分,共20分)
19.一个几何体是由棱长为1的小立方体搭建而成的,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方体的个数.
(1)画出该几何体的主视图和左视图;
(2)求该几何体的体积和表面积.
20.如图,电线杆上有一盏路灯,电线杆与三个等高的标杆整齐地排列在笔直的马路一侧,AB,CD,EF是三个标杆,相邻的两个标杆之间的距离都是2 m,已知AB,CD在灯光下的影长分别为BM=1.6 m,DN=0.6 m.
(1)请画出路灯的位置和标杆EF在路灯灯光下的影子;
(2)求标杆EF的影长.
六、(本题满分12分)
21.如图,用10个大小相同的小正方体搭成一个组合体.
(1)请在指定位置画出该组合体的左视图、俯视图;
(2)在不改变该组合体中小正方体个数的前提下,从中移动一个小正方体,使所得新组合体与原组合体相比,左视图、俯视图形状保持不变,但主视图的形状改变,请画出新组合体主视图的所有可能的形状.(所给的方格图不一定全用,不够可添)
七、(本题满分12分)
22.如图是由两个长方体组合而成的一个几何体的三视图,根据图中所标尺寸(单位:mm),计算这个几何体的表面积.
八、(本题满分14分)
23.一透明的敞口正方体容器ABCD A′B′C′D′中装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α).
探究:如图①,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②所示.解决问题:
(1)CQ与BE的位置关系是________,BQ的长是________dm;
(2)求液体的体积;[参考算法:直三棱柱体积(V液)=底面积(S△BCQ)×高(AB)]
(3)求液面到桌面的高度和倾斜角α的度数.(注:sin 37°≈,tan 37°≈)
答案
一、1.A 2.D 3.B 4.D 5.B 6.B 7.A 8.D 9.B 10.D
二、11.平行投影 12.4 13.240
14.(1)x+2 (2)x2-2x
三、15.解:如图所示.
16.解:(1)当阳光垂直照射地面时,标杆在地面上的投影是一个点.
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是线段BC,如图所示.
四、17.解:由题意得圆锥的底面圆的半径为1 cm,
∴π×12=π(cm2).
∴其俯视图的面积为π cm2.
18.解:过点A作AM⊥DE于点M,交BC于点N,则AN⊥BC.
由题意得BC∥DE,
∴△ABC∽△ADE.
∴=,
即=.
∴BC=0.16 m=16 cm,
即灯罩的直径为16 cm.
五、19.解:(1)如图所示.
(2)体积:1×1×1×(2+2+3+1)=8.
表面积:1×1×(6×2+4×2+5×2)=30.
20.解:(1)如图所示,O处为路灯的位置,标杆EF在路灯灯光下的影子为FP.
(2)如图,连接AE,由题意可知点C在AE上.设FP的长度为x m,易知=,=,
∴=,
即=,
解得x=0.4.
经检验,x=0.4是方程的解且符合题意,
∴标杆EF的影长为0.4 m.
六、21.解:(1)如图①所示.
(2)如图②所示.
七、22.解:S表=(6×8+6×2+2×8+4×4+4×2)×2=200(mm2),即这个几何体的表面积为200 mm2.
八、23.解:(1)平行;3
(2)V液=×3×4×4=24(dm3).
(3)过点B作BF⊥CQ,垂足为F.
∵×3×4=×5×BF,
∴BF= dm.
∴液面到桌面的高度是 dm.
在Rt△BCQ中,∵tan ∠BCQ=,
∴α=∠BCQ≈37°.
