人教版 九年级上册 第二十三章 旋转 综合测试题 (含解析)
文档属性
| 名称 | 人教版 九年级上册 第二十三章 旋转 综合测试题 (含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 227.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 00:00:00 | ||
图片预览

文档简介
人教版九年级第二十三章综合测试题
(满分120分,时间100分钟)
一、选择题(每题3分,满分30分)
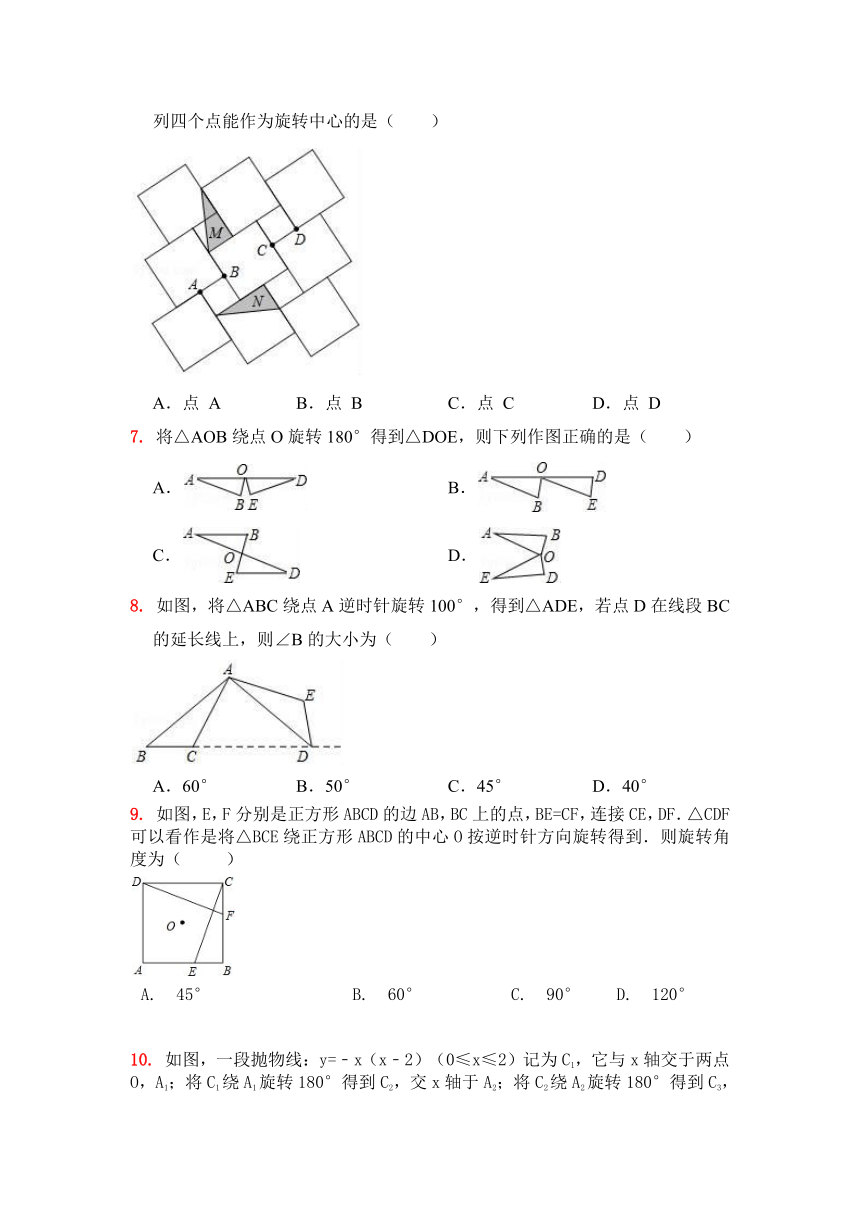
1. 下列图形绕某点旋转90°后,不能与原来图形重合的是( )
A. B.
C. D.
2. 如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是( )
A.(﹣1,2) B.(2,﹣1) C.(1,﹣2) D.(﹣2,1)
3. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
4. 如图图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5. 已知点A(a,﹣1)与B(2,b)是关于原点O的对称点,则( )
A.a=﹣2,b=﹣1 B.a=﹣2,b=1 C.a=2,b=﹣1 D.a=2,b=1
6. 若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是( )
A.点 A B.点 B C.点 C D.点 D
7. 将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A. B.
C. D.
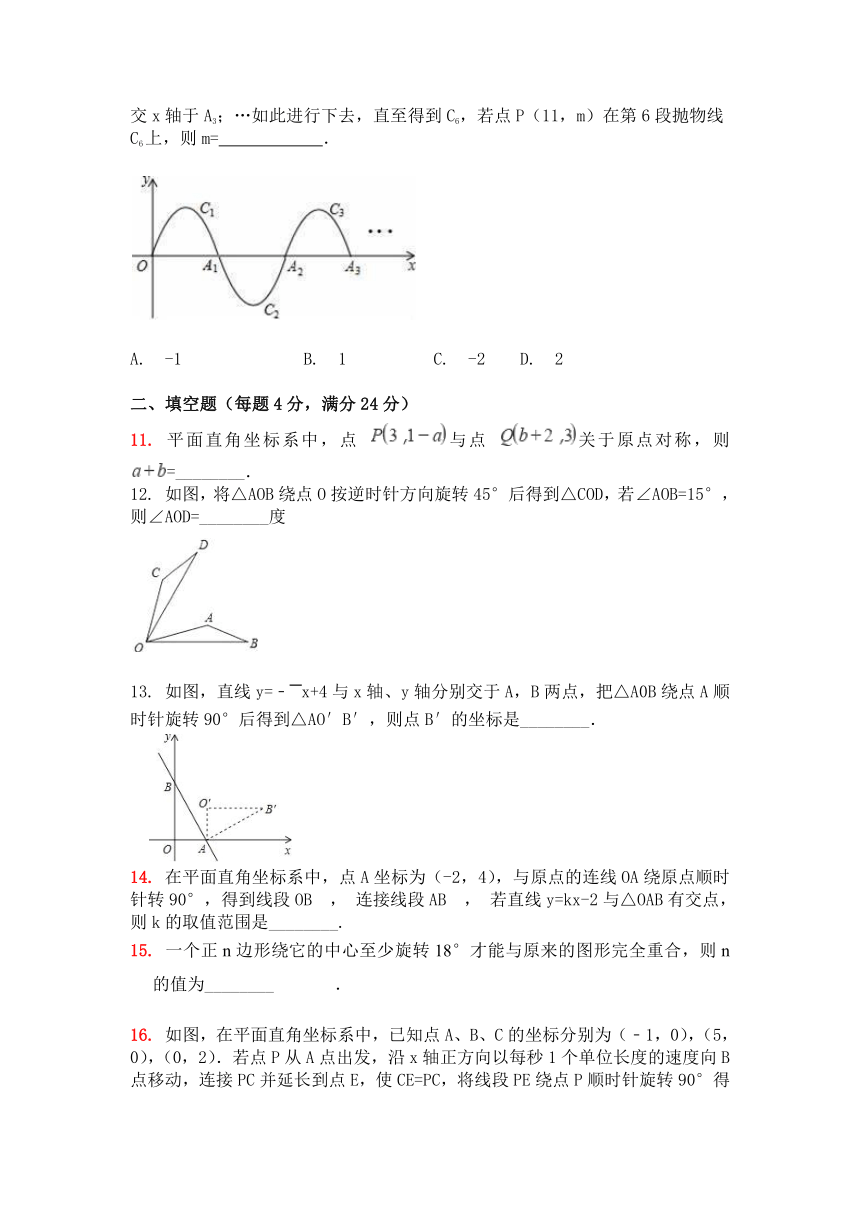
8. 如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为( )
A.60° B.50° C.45° D.40°
9. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
A. 45° B. 60° C. 90° D. 120°
10. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
A. -1 B. 1 C. -2 D. 2
二、填空题(每题4分,满分24分)
11. 平面直角坐标系中,点 与点 关于原点对称,则 =________.
12. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=________度
13. 如图,直线y=﹣x+4与x轴、y轴分别交于A,B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是________.
14. 在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB , 连接线段AB , 若直线y=kx-2与△OAB有交点,则k的取值范围是________.
15. 一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为________ .
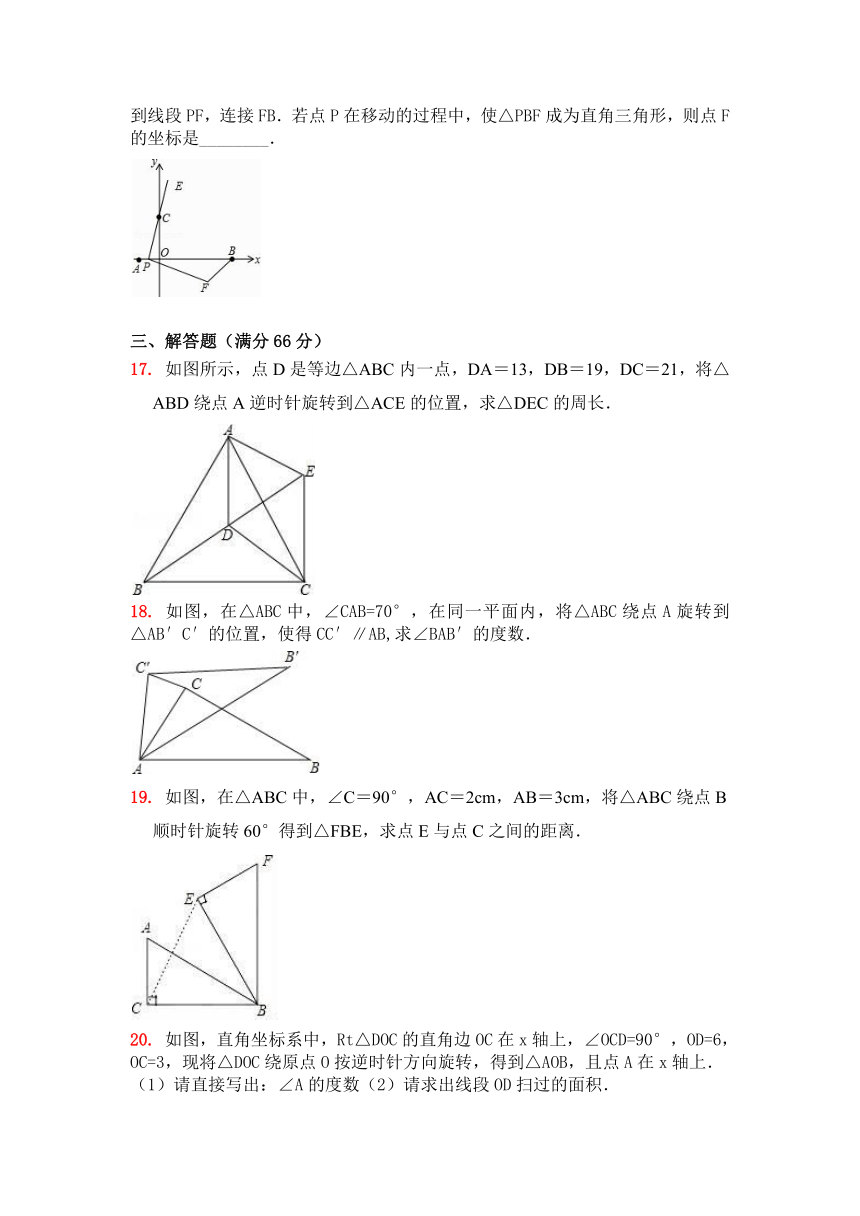
16. 如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是________.
三、解答题(满分66分)
17. 如图所示,点D是等边△ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.
18. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.
19. 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,求点E与点C之间的距离.
20. 如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数(2)请求出线段OD扫过的面积.
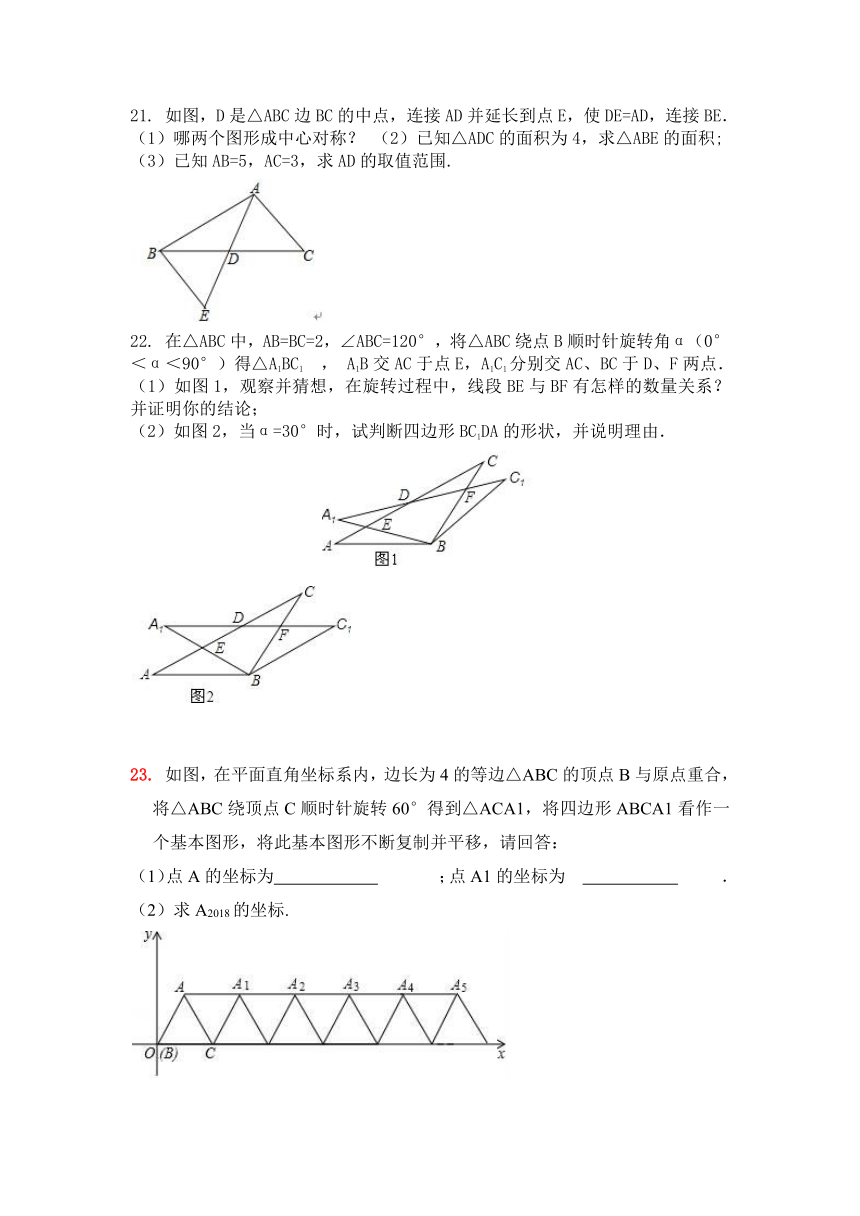
21. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称? (2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
22. 在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
23. 如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)点A的坐标为 ;点A1的坐标为 .
(2)求A2018的坐标.
24. 如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
参考答案
答案:
选择题
1. A、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
B、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
C、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
D、绕它的中心旋转120°才能与原图形重合,故本选项符合题意.
故选:D.
2. 将A点绕原点O逆时针旋转90°得到A1,
即将Rt△OBA点绕原点O逆时针旋转90°得到Rt△OB1A1,如图,
所以OB1=OB=2,A1B1=AB=1,
所以点A1的坐标是(﹣1,2).
故选:A.
3. 根据中心对称的概念,知②③④都是中心对称.
故选:C.
4. A、是轴对称图形,不是中心对称图形,不合题意;
B、不是轴对称图形,是中心对称图形,不合题意;
C、是轴对称图形,不是中心对称图形,不合题意;
D、是轴对称图形,也是中心对称图形,符合题意.
故选:D.
5.∵点A(a,﹣1)与点B(2,b)是关于原点O的对称点,
∴a=﹣2,b=1,
故选:B.
6. 如图所示:三角形M绕点C经过逆时针旋转变换能得到三角形N,
故选:C.
7. ∵△AOB绕点O旋转180°得到△DOE,
∴作图正确是C选项图形.
故选:C.
8. 根据旋转的性质,可得:AB=AD,∠BAD=100°,
∴∠B=∠ADB=×(180°﹣100°)=40°.
故选:D.
9. 将△CBE绕正方形的对角线交点O按顺时针方向旋转到△CDF时,C和D重合,
即∠COD是旋转角,
∵四边形ABCD是正方形,
∴∠OCD=∠ODC=45°,
∴∠COD=180°-45°-45°=90°,
即旋转角是90°,
故答案为90 .
10. ∵y=﹣x(x﹣2)(0≤x≤2),
∴配方可得y=﹣(x﹣1)2+1(0≤x≤2),
∴顶点坐标为(1,1),
∴A1坐标为(2,0)
∵C2由C1旋转得到,
∴OA1=A1A2,即C2顶点坐标为(3,﹣1),A2(4,0);
照此类推可得,C3顶点坐标为(5,1),A3(6,0);
C4顶点坐标为(7,﹣1),A4(8,0);
C5顶点坐标为(9,1),A5(10,0);
C6顶点坐标为(11,﹣1),A6(12,0);
∴m=﹣1.
故答案为:A
填空题
11.-1 提示:1-a=-3,b+2=-3, ∴a=4,b=-5, ∴a+b=-1
12. C∵将△AOB绕点O按逆时针方向旋转60°后得到△COD,
∴∠BOD=60°,∵∠AOB=15°,∴∠AOD=∠DOB-∠AOB=60°-15°=45°.
13. 直线y=﹣x+4与x轴,y轴分别交于A(3,0),B(0,4)两点.旋转前后三角形全等.
由图易知点B′的纵坐标为OA长,即为3,即横坐标为OA+OB=OA+O′B′=3+4=7.
故点B′的坐标是(7,3)
14.
如图,点A(-2,4)绕原点顺时针转90°后的对应点B的坐标为(4,2),
直线经过点A时,-2k-2=4,
解得k=-3,
直线经过点B时,4k-2=2,
解得k=1,
所以,直线y=kx-2与△OAB有交点时k的取值范围是k≤-3或k≥1.
故答案为:k≤-3或k≥1
15.20 提示:n=360/18=20
16. (5,2),( , )提示:①若F为直角顶点,过F作FD⊥x轴于D,由(2)可知BP=6-t,DP=2OC=4,
在Rt△OCP中,OP=t-1,
由勾股定理易求得CP 2 =t 2 -2t+5,那
么PF 2 =(2CP) 2 =4(t 2 -2t+5);
在Rt△PFB中,FD⊥PB,
由射影定理可求得PB=PF 2 ÷PD=t 2 -2t+5,
而PB的另一个表达式为:PB=6-t,
联立两式可得t 2 -2t+5=6-t,即t=
②B为直角顶点,△PFB ∽ △CPO,且相似比为2,
那么BP=2OC=4,即OP=OB-BP=1,此时t=2,
P点坐标为(1,0).FD=2(t-1)=2,
则F点坐标为(5,2)
解答题
17. 解:∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵△ABD绕点A逆时针旋转到△ACE的位置,
∴AD=AE,CE=BD=19,∠DAE=∠BAC=60°,
∴△ADE为等边三角形,
∴DE=AD=13,
∴△DEC的周长=DE+DC+CE=13+21+19=53.
18.∵CC′∥AB ,
∴∠A CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
19. 解:连接EC,即线段EC的长是点E与点C之间的距离,
在Rt△ACB中,由勾股定理得:BC===
将△ABC绕点B顺时针旋转60°得到△FBE,
∴BC=BE,∠CBE=60°
∴△BEC是等边三角形
∴EC=BE=BC=
20. 在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴sin∠D=.
∴∠D=30°,
由旋转的性质可知:∠A=∠D=30°.
(2)在Rt△DOC,∠OCD=90°,∠D=30°,
∴∠DOC=60°,
∴∠AOD=180°﹣60°=120°,
∴线段OD扫过的面积为.
21. 解:(1)∵将△ACD旋转后能与△EBD重合,
∴旋转中心是点D,旋转了180度;
故答案为:D,180;
(2)∵将△ACD旋转后能与△EBD重合,
∴BE=AC=4,DE=AD,
在△ABE中,由三角形的三边关系得,AB﹣BE<AE<AB+BE,
∵AB=7,
∴3<AE<11,即3<2AD<11,
∴1.5<AD<5.5,
即中线AD长的取值范围是1.5<AD<5.5.
22.
解:(1)EA1=FC;
证明:∵AB=BC,
∴∠∠A=∠C,
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF,
∴BE=BF,
又∵BA1=BC,
∴BA1-BE=BC-BF,即EA1=FC;
(2)四边形BC1DA是菱形;理由:
∵∠A1=∠ABA1=30°,
∴A1C1∥AB,同理AC∥BC1,
∴四边形BC1DA是平行四边形,
又∵AB=BC1,
∴四边形BC1DA是菱形
23. 解:(1)∵边长为4的等边△ABC的顶点B与原点重合,
∴OA=BC=4,∠AOC=60°.
如图,过点A作AD⊥x轴于点D,
∴BD=DC=BC=2,AD=2,
∴点A的坐标为(2,2).
∵将△ABC绕顶点C顺时针旋转60°得到△ACA1,
∴四边形ABCA1是平行四边形,
∴AA1=BC=4,AA1∥BC,
∴点A1的坐标为(2+4,2),即(6,2).
故答案为:(2,2);(6,2).
(2)∵将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,
∴点A2的坐标为(2+4×2,2),即(10,2);点A3的坐标为(2+4×3,2),即(14,2);……;
∴点A2018的坐标为(2+4×2018,2),即(8074,2).
故答案为:(8074,2).
24. (1)
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
(2)①成立,
证明:如图2,
延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
②不同,猜想:AF+AB=BE,
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AF+AB=BE.
(满分120分,时间100分钟)
一、选择题(每题3分,满分30分)
1. 下列图形绕某点旋转90°后,不能与原来图形重合的是( )
A. B.
C. D.
2. 如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是( )
A.(﹣1,2) B.(2,﹣1) C.(1,﹣2) D.(﹣2,1)
3. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
4. 如图图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5. 已知点A(a,﹣1)与B(2,b)是关于原点O的对称点,则( )
A.a=﹣2,b=﹣1 B.a=﹣2,b=1 C.a=2,b=﹣1 D.a=2,b=1
6. 若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是( )
A.点 A B.点 B C.点 C D.点 D
7. 将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A. B.
C. D.
8. 如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为( )
A.60° B.50° C.45° D.40°
9. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
A. 45° B. 60° C. 90° D. 120°
10. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
A. -1 B. 1 C. -2 D. 2
二、填空题(每题4分,满分24分)
11. 平面直角坐标系中,点 与点 关于原点对称,则 =________.
12. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=________度
13. 如图,直线y=﹣x+4与x轴、y轴分别交于A,B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是________.
14. 在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB , 连接线段AB , 若直线y=kx-2与△OAB有交点,则k的取值范围是________.
15. 一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为________ .
16. 如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是________.
三、解答题(满分66分)
17. 如图所示,点D是等边△ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.
18. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.
19. 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,求点E与点C之间的距离.
20. 如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数(2)请求出线段OD扫过的面积.
21. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称? (2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
22. 在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
23. 如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)点A的坐标为 ;点A1的坐标为 .
(2)求A2018的坐标.
24. 如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
参考答案
答案:
选择题
1. A、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
B、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
C、绕它的中心旋转90°能与原图形重合,故本选项不合题意;
D、绕它的中心旋转120°才能与原图形重合,故本选项符合题意.
故选:D.
2. 将A点绕原点O逆时针旋转90°得到A1,
即将Rt△OBA点绕原点O逆时针旋转90°得到Rt△OB1A1,如图,
所以OB1=OB=2,A1B1=AB=1,
所以点A1的坐标是(﹣1,2).
故选:A.
3. 根据中心对称的概念,知②③④都是中心对称.
故选:C.
4. A、是轴对称图形,不是中心对称图形,不合题意;
B、不是轴对称图形,是中心对称图形,不合题意;
C、是轴对称图形,不是中心对称图形,不合题意;
D、是轴对称图形,也是中心对称图形,符合题意.
故选:D.
5.∵点A(a,﹣1)与点B(2,b)是关于原点O的对称点,
∴a=﹣2,b=1,
故选:B.
6. 如图所示:三角形M绕点C经过逆时针旋转变换能得到三角形N,
故选:C.
7. ∵△AOB绕点O旋转180°得到△DOE,
∴作图正确是C选项图形.
故选:C.
8. 根据旋转的性质,可得:AB=AD,∠BAD=100°,
∴∠B=∠ADB=×(180°﹣100°)=40°.
故选:D.
9. 将△CBE绕正方形的对角线交点O按顺时针方向旋转到△CDF时,C和D重合,
即∠COD是旋转角,
∵四边形ABCD是正方形,
∴∠OCD=∠ODC=45°,
∴∠COD=180°-45°-45°=90°,
即旋转角是90°,
故答案为90 .
10. ∵y=﹣x(x﹣2)(0≤x≤2),
∴配方可得y=﹣(x﹣1)2+1(0≤x≤2),
∴顶点坐标为(1,1),
∴A1坐标为(2,0)
∵C2由C1旋转得到,
∴OA1=A1A2,即C2顶点坐标为(3,﹣1),A2(4,0);
照此类推可得,C3顶点坐标为(5,1),A3(6,0);
C4顶点坐标为(7,﹣1),A4(8,0);
C5顶点坐标为(9,1),A5(10,0);
C6顶点坐标为(11,﹣1),A6(12,0);
∴m=﹣1.
故答案为:A
填空题
11.-1 提示:1-a=-3,b+2=-3, ∴a=4,b=-5, ∴a+b=-1
12. C∵将△AOB绕点O按逆时针方向旋转60°后得到△COD,
∴∠BOD=60°,∵∠AOB=15°,∴∠AOD=∠DOB-∠AOB=60°-15°=45°.
13. 直线y=﹣x+4与x轴,y轴分别交于A(3,0),B(0,4)两点.旋转前后三角形全等.
由图易知点B′的纵坐标为OA长,即为3,即横坐标为OA+OB=OA+O′B′=3+4=7.
故点B′的坐标是(7,3)
14.
如图,点A(-2,4)绕原点顺时针转90°后的对应点B的坐标为(4,2),
直线经过点A时,-2k-2=4,
解得k=-3,
直线经过点B时,4k-2=2,
解得k=1,
所以,直线y=kx-2与△OAB有交点时k的取值范围是k≤-3或k≥1.
故答案为:k≤-3或k≥1
15.20 提示:n=360/18=20
16. (5,2),( , )提示:①若F为直角顶点,过F作FD⊥x轴于D,由(2)可知BP=6-t,DP=2OC=4,
在Rt△OCP中,OP=t-1,
由勾股定理易求得CP 2 =t 2 -2t+5,那
么PF 2 =(2CP) 2 =4(t 2 -2t+5);
在Rt△PFB中,FD⊥PB,
由射影定理可求得PB=PF 2 ÷PD=t 2 -2t+5,
而PB的另一个表达式为:PB=6-t,
联立两式可得t 2 -2t+5=6-t,即t=
②B为直角顶点,△PFB ∽ △CPO,且相似比为2,
那么BP=2OC=4,即OP=OB-BP=1,此时t=2,
P点坐标为(1,0).FD=2(t-1)=2,
则F点坐标为(5,2)
解答题
17. 解:∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵△ABD绕点A逆时针旋转到△ACE的位置,
∴AD=AE,CE=BD=19,∠DAE=∠BAC=60°,
∴△ADE为等边三角形,
∴DE=AD=13,
∴△DEC的周长=DE+DC+CE=13+21+19=53.
18.∵CC′∥AB ,
∴∠A CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
19. 解:连接EC,即线段EC的长是点E与点C之间的距离,
在Rt△ACB中,由勾股定理得:BC===
将△ABC绕点B顺时针旋转60°得到△FBE,
∴BC=BE,∠CBE=60°
∴△BEC是等边三角形
∴EC=BE=BC=
20. 在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴sin∠D=.
∴∠D=30°,
由旋转的性质可知:∠A=∠D=30°.
(2)在Rt△DOC,∠OCD=90°,∠D=30°,
∴∠DOC=60°,
∴∠AOD=180°﹣60°=120°,
∴线段OD扫过的面积为.
21. 解:(1)∵将△ACD旋转后能与△EBD重合,
∴旋转中心是点D,旋转了180度;
故答案为:D,180;
(2)∵将△ACD旋转后能与△EBD重合,
∴BE=AC=4,DE=AD,
在△ABE中,由三角形的三边关系得,AB﹣BE<AE<AB+BE,
∵AB=7,
∴3<AE<11,即3<2AD<11,
∴1.5<AD<5.5,
即中线AD长的取值范围是1.5<AD<5.5.
22.
解:(1)EA1=FC;
证明:∵AB=BC,
∴∠∠A=∠C,
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF,
∴BE=BF,
又∵BA1=BC,
∴BA1-BE=BC-BF,即EA1=FC;
(2)四边形BC1DA是菱形;理由:
∵∠A1=∠ABA1=30°,
∴A1C1∥AB,同理AC∥BC1,
∴四边形BC1DA是平行四边形,
又∵AB=BC1,
∴四边形BC1DA是菱形
23. 解:(1)∵边长为4的等边△ABC的顶点B与原点重合,
∴OA=BC=4,∠AOC=60°.
如图,过点A作AD⊥x轴于点D,
∴BD=DC=BC=2,AD=2,
∴点A的坐标为(2,2).
∵将△ABC绕顶点C顺时针旋转60°得到△ACA1,
∴四边形ABCA1是平行四边形,
∴AA1=BC=4,AA1∥BC,
∴点A1的坐标为(2+4,2),即(6,2).
故答案为:(2,2);(6,2).
(2)∵将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,
∴点A2的坐标为(2+4×2,2),即(10,2);点A3的坐标为(2+4×3,2),即(14,2);……;
∴点A2018的坐标为(2+4×2018,2),即(8074,2).
故答案为:(8074,2).
24. (1)
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
(2)①成立,
证明:如图2,
延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
②不同,猜想:AF+AB=BE,
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AF+AB=BE.
同课章节目录
