2.2.1对数与对数运算(第一课时)
文档属性
| 名称 | 2.2.1对数与对数运算(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 357.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-28 16:31:01 | ||
图片预览








文档简介
课件24张PPT。2.2.1 对数与对数的运算 (第一课时)1、如果我国GDP平均每年增长8%,则经过多少年我国的GDP是现在的两倍? 解:设经过x年国民生产总值是现在的两倍,令现在的国民生产总值为a. 依题意得: 即:?知识引入2、求下列各式中x的值?.72)3( .16)41)(2( .322 )1(===xxx知识引入第 1、2 题有什么共同特点?已知底数和幂的值,求指数。其中a叫做对数的底数, N叫做真数. 1.对数的定义: 一般地,如果ax=N ( a > 0 , 且a ≠ 1 )那么数x叫做以a为底N的对数,记作: 讲授新课 为什么在定义中要规定:底数a>0且a≠1;N >0。探讨(1)若a<0,则N取某些数值时,logaN不存在
因此,规定a不能小于0.为什么对数logaN只有在a>0且a≠1时才有意义呢?因此,规定a≠0.探究一:因此,规定a≠1综上所述,对数符号logaN只有在a>0且a≠1时才有意义 练习1:将下列指数式写成对数式:以5为底25的对数是2,
记作64126=-讲授新课以2为底 的对数是-6,
记作以2为底7的对数是x,
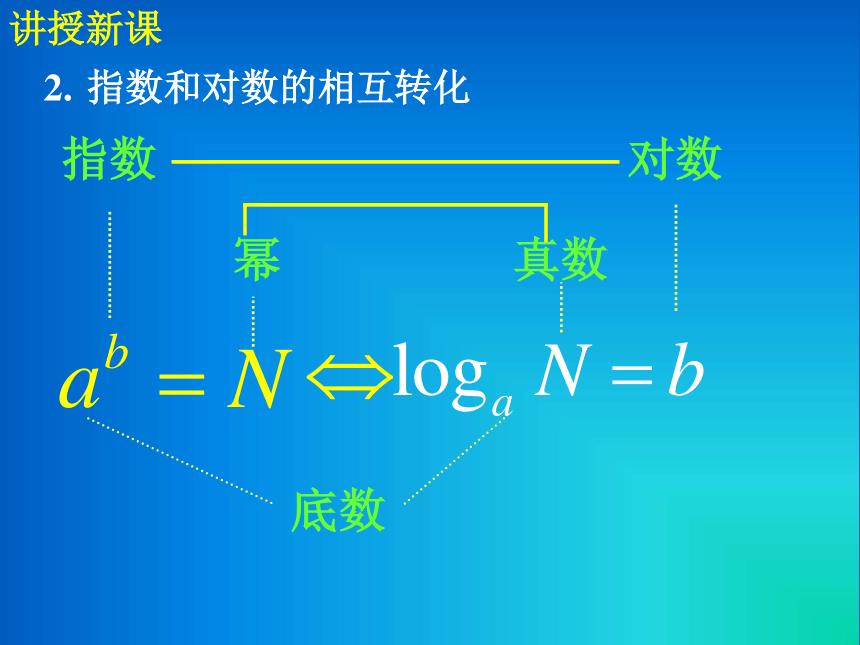
记作①③②思考:对数与指数有什么区别与联系?名称式子axN底数底数指数对数幂真数讲授新课底数幂真数指数对数指数和对数的相互转化讲授新课?3.两个重要的对数:(1)常用对数:以10为底的对数 。
简记作 。如 简记为(2)自然对数:
以无理数e = 2.71828…为底的对数 。
简记作 。如 简记为讲授新课例1.将下列指数式写成对数式: 5.73)31((4)2710(3)b1e(2)6255(1)ma64====-解: 例题分析(练习:课本P64 1)例2.将下列对数式写成指数式: 解:例题分析(练习:课本P64 2)例3 求下列各式中的x的值例题分析3、运用指数运算求值讲授新课4.对数的性质结论:零和负数没有对数探究活动
(1)、试求下列各式的值:讲授新课4.对数的性质探究活动
(2)、求下列各式的值:思考:你发现了什么?讲授新课探究活动
(3)、求下列各式的值:思考:你发现了什么?4.对数的性质讲授新课探究活动
(4)、求下列各式的值:思考:你发现了什么?4.对数的性质讲授新课探究活动
(5)、求下列各式的值:思考:你发现了什么?课堂练习:P64,练习3、44.对数的性质讲授新课4.对数的性质(1)负数和零没有对数(∵在指数式中 N > 0 ) 即:1的对数是0即:底数的对数是1(4)对数恒等式: (5)对数恒等式:.结论:巩固练习D 2、 对数式中x的取值范围是______3.求下列各式的值(1) (2) (3) (4) 巩固练习ab=N=alogaN=b底数方根底数指数根指数对数幂被开方数真数乘方,
由a,b求N开方,
由N,b求a对数,
由a,N求b比较指数式、根式、对数式:(1)开方运算、对数运算都是指数运算的逆运算。(2)弄清对数式与指数式的互换是掌握对数意义及运算的关键表达形式abN对应的运算1、对数的定义2、指数式和对数式的互换; 一般地, ax=N(a>0,a≠1),那么数x叫做以a为底 N的对数, 记作logaN=x。(式中的a叫做对数的底数,N叫做真数.)归纳小结思考:各位同学在这节课上有什么收获?归纳小结(1)负数和零没有对数即:1的对数是0即:底数的对数是14、对数的性质3、运用指数运算求值布置作业作业:P74 习题A组 1、2
因此,规定a不能小于0.为什么对数logaN只有在a>0且a≠1时才有意义呢?因此,规定a≠0.探究一:因此,规定a≠1综上所述,对数符号logaN只有在a>0且a≠1时才有意义 练习1:将下列指数式写成对数式:以5为底25的对数是2,
记作64126=-讲授新课以2为底 的对数是-6,
记作以2为底7的对数是x,
记作①③②思考:对数与指数有什么区别与联系?名称式子axN底数底数指数对数幂真数讲授新课底数幂真数指数对数指数和对数的相互转化讲授新课?3.两个重要的对数:(1)常用对数:以10为底的对数 。
简记作 。如 简记为(2)自然对数:
以无理数e = 2.71828…为底的对数 。
简记作 。如 简记为讲授新课例1.将下列指数式写成对数式: 5.73)31((4)2710(3)b1e(2)6255(1)ma64====-解: 例题分析(练习:课本P64 1)例2.将下列对数式写成指数式: 解:例题分析(练习:课本P64 2)例3 求下列各式中的x的值例题分析3、运用指数运算求值讲授新课4.对数的性质结论:零和负数没有对数探究活动
(1)、试求下列各式的值:讲授新课4.对数的性质探究活动
(2)、求下列各式的值:思考:你发现了什么?讲授新课探究活动
(3)、求下列各式的值:思考:你发现了什么?4.对数的性质讲授新课探究活动
(4)、求下列各式的值:思考:你发现了什么?4.对数的性质讲授新课探究活动
(5)、求下列各式的值:思考:你发现了什么?课堂练习:P64,练习3、44.对数的性质讲授新课4.对数的性质(1)负数和零没有对数(∵在指数式中 N > 0 ) 即:1的对数是0即:底数的对数是1(4)对数恒等式: (5)对数恒等式:.结论:巩固练习D 2、 对数式中x的取值范围是______3.求下列各式的值(1) (2) (3) (4) 巩固练习ab=N=alogaN=b底数方根底数指数根指数对数幂被开方数真数乘方,
由a,b求N开方,
由N,b求a对数,
由a,N求b比较指数式、根式、对数式:(1)开方运算、对数运算都是指数运算的逆运算。(2)弄清对数式与指数式的互换是掌握对数意义及运算的关键表达形式abN对应的运算1、对数的定义2、指数式和对数式的互换; 一般地, ax=N(a>0,a≠1),那么数x叫做以a为底 N的对数, 记作logaN=x。(式中的a叫做对数的底数,N叫做真数.)归纳小结思考:各位同学在这节课上有什么收获?归纳小结(1)负数和零没有对数即:1的对数是0即:底数的对数是14、对数的性质3、运用指数运算求值布置作业作业:P74 习题A组 1、2
