2022-2023学年沪科版七年级数学上册 3.2 一元一次方程的应用 第1课时 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册 3.2 一元一次方程的应用 第1课时 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 13:12:42 | ||
图片预览




文档简介
(共15张PPT)
3.2 一元一次方程的应用
第1课时 等积与行程问题
等积变形和行程问题
学习目标
1. 能用一元一次方程解决等积变形和行程问题.
2. 能分析出实际问题中的数量关系,并根据等量关系列出方程.
3. 通过对实际问题的分析、解决,感受方程作为刻画现实世界的有效
模型的意义,培养学生分析问题、解决问题的能力.
4. 通过列方程解决实际问题,培养学生应用数学的能力,体会数学与
实际生活的联系.
传说,古希腊的一位国王让金匠给他制作了一顶纯金的皇冠,国王怀疑皇冠中掺了白银,于是让阿基米德检验一下,阿基米德苦思冥想了很长时间,才找到了测量皇冠体积的办法.
情境引入
你知道是什么方法吗?
等积问题
典型例题
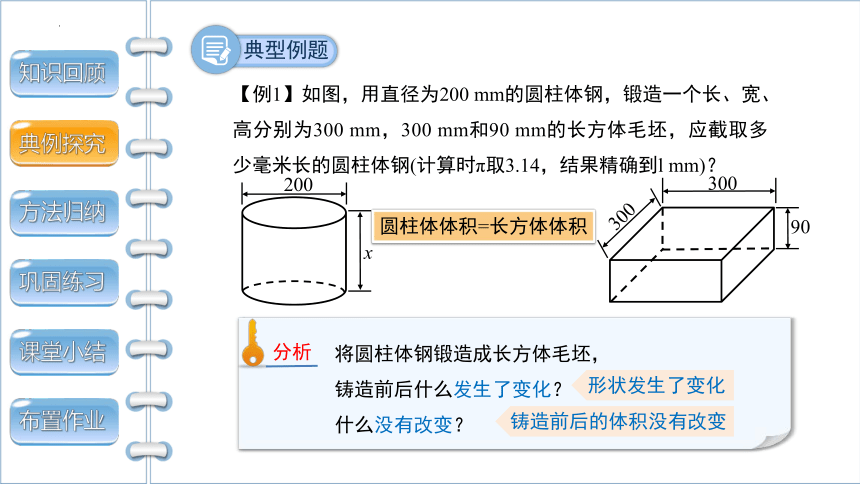
【例1】如图,用直径为200 mm的圆柱体钢,锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到l mm)?
200
x
300
90
300
将圆柱体钢锻造成长方体毛坯,
铸造前后什么发生了变化?
什么没有改变?
分析
形状发生了变化
铸造前后的体积没有改变
圆柱体体积=长方体体积
典型例题
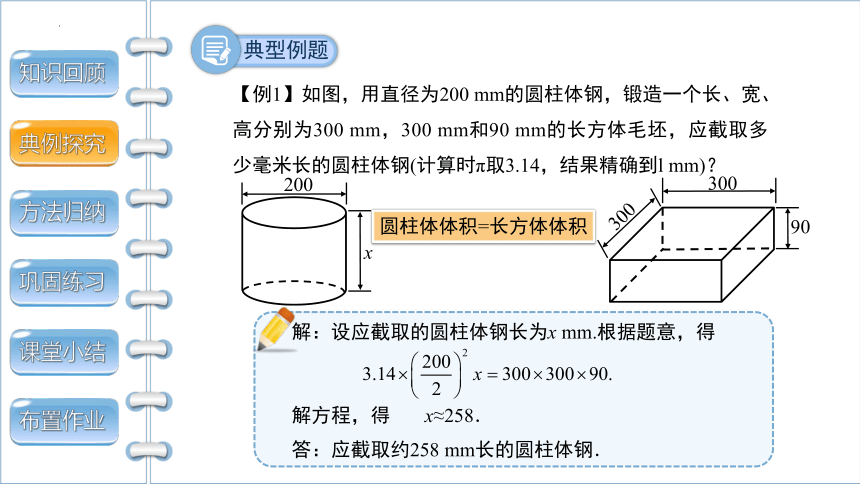
【例1】如图,用直径为200 mm的圆柱体钢,锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到l mm)?
解方程,得 x≈258.
解:设应截取的圆柱体钢长为x mm.根据题意,得
答:应截取约258 mm长的圆柱体钢.
200
x
300
90
300
圆柱体体积=长方体体积
典型例题
【例2】为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
行程问题中常涉及的量有哪些?
分析
这些量之间有什么基本关系?
路程
平均速度
时间
路程=平均速度×时间
典型例题
【例2】为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40)km.客车行驶路程1110 km,平均速度是(x+40)km/h,所需时间是10 h.根据题意,得
10(x+40)=1110
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
路程=平均速度×时间
归纳
列方程解应用题的一般步骤:
审题:弄清问题中的已知量和未知量,找出等量关系;
设未知数:设直接未知数或设间接未知数,哪种简单用哪种;
列方程:根据已知量和未知量之间的等量关系,列出方程;
解方程:解方程求出未知数的值;
检验并写出答案:检验所得的值是否正确和符合实际情形,
并写出答案(包括单位名称).
1
2
3
4
5
归纳
列一元一次方程解应用题的基本过程:
实际
问题
一元一次
方程
一元一次
方程的解
实际问题的答案
解方程
检验解是否符合题意
抽象出
数学模型
ds
1.用直径为4 cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2 cm,高为16 cm的圆柱形零件,则需要截取多长的圆钢?
随堂练习
解:设需要截取x cm的圆钢.根据题意,得
π×2 x=3×π×2 ×16.
解方程,得 x=12.
答:需要截取12 cm的圆钢.
随堂练习
2.在铁路线上有A,B两站,它们之间的距离为360 km,一列货车从B站开出,每小时行驶160 km,货车开出30 min后,一列动车从A站开出,每小时行驶240 km,两车同向而行,动车在货车后面,问动车开出后多少小时追上货车?
360 km
货车:160 km/h
动车:240 km/h
货车先行驶30 min的路程
A
B
D
C
相遇处
等量关系: 360km + 货车行驶的路程 = 动车行驶的路程
分析:行程问题中的等量关系,可以借助线段示意图.
随堂练习
2.在铁路线上有A,B两站,它们之间的距离为360 km,一列货车从B站开出,每小时行驶160 km,货车开出30 min后,一列动车从A站开出,每小时行驶240 km,两车同向而行,动车在货车后面,问动车开出后多少小时追上货车?
解方程,得
解:动车开出后x小时追上货车.根据题意,得
答:动车开出 h后追上货车.
等量关系: 360km + 货车行驶的路程 = 动车行驶的路程
等积变形和行程问题
列方程解应用题的一般步骤:
基本思路:
审题
设未知数
列方程
解方程
检验并写出答案
关键:弄清题意,找出相等关系.
实际
问题
一元一次
方程
一元一次
方程的解
实际问题的答案
解方程
检验解是否符合题意
抽象出
数学模型
教科书
第94页 练习
第1、2、3题
再见
3.2 一元一次方程的应用
第1课时 等积与行程问题
等积变形和行程问题
学习目标
1. 能用一元一次方程解决等积变形和行程问题.
2. 能分析出实际问题中的数量关系,并根据等量关系列出方程.
3. 通过对实际问题的分析、解决,感受方程作为刻画现实世界的有效
模型的意义,培养学生分析问题、解决问题的能力.
4. 通过列方程解决实际问题,培养学生应用数学的能力,体会数学与
实际生活的联系.
传说,古希腊的一位国王让金匠给他制作了一顶纯金的皇冠,国王怀疑皇冠中掺了白银,于是让阿基米德检验一下,阿基米德苦思冥想了很长时间,才找到了测量皇冠体积的办法.
情境引入
你知道是什么方法吗?
等积问题
典型例题
【例1】如图,用直径为200 mm的圆柱体钢,锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到l mm)?
200
x
300
90
300
将圆柱体钢锻造成长方体毛坯,
铸造前后什么发生了变化?
什么没有改变?
分析
形状发生了变化
铸造前后的体积没有改变
圆柱体体积=长方体体积
典型例题
【例1】如图,用直径为200 mm的圆柱体钢,锻造一个长、宽、高分别为300 mm,300 mm和90 mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到l mm)?
解方程,得 x≈258.
解:设应截取的圆柱体钢长为x mm.根据题意,得
答:应截取约258 mm长的圆柱体钢.
200
x
300
90
300
圆柱体体积=长方体体积
典型例题
【例2】为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
行程问题中常涉及的量有哪些?
分析
这些量之间有什么基本关系?
路程
平均速度
时间
路程=平均速度×时间
典型例题
【例2】为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40)km.客车行驶路程1110 km,平均速度是(x+40)km/h,所需时间是10 h.根据题意,得
10(x+40)=1110
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
路程=平均速度×时间
归纳
列方程解应用题的一般步骤:
审题:弄清问题中的已知量和未知量,找出等量关系;
设未知数:设直接未知数或设间接未知数,哪种简单用哪种;
列方程:根据已知量和未知量之间的等量关系,列出方程;
解方程:解方程求出未知数的值;
检验并写出答案:检验所得的值是否正确和符合实际情形,
并写出答案(包括单位名称).
1
2
3
4
5
归纳
列一元一次方程解应用题的基本过程:
实际
问题
一元一次
方程
一元一次
方程的解
实际问题的答案
解方程
检验解是否符合题意
抽象出
数学模型
ds
1.用直径为4 cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2 cm,高为16 cm的圆柱形零件,则需要截取多长的圆钢?
随堂练习
解:设需要截取x cm的圆钢.根据题意,得
π×2 x=3×π×2 ×16.
解方程,得 x=12.
答:需要截取12 cm的圆钢.
随堂练习
2.在铁路线上有A,B两站,它们之间的距离为360 km,一列货车从B站开出,每小时行驶160 km,货车开出30 min后,一列动车从A站开出,每小时行驶240 km,两车同向而行,动车在货车后面,问动车开出后多少小时追上货车?
360 km
货车:160 km/h
动车:240 km/h
货车先行驶30 min的路程
A
B
D
C
相遇处
等量关系: 360km + 货车行驶的路程 = 动车行驶的路程
分析:行程问题中的等量关系,可以借助线段示意图.
随堂练习
2.在铁路线上有A,B两站,它们之间的距离为360 km,一列货车从B站开出,每小时行驶160 km,货车开出30 min后,一列动车从A站开出,每小时行驶240 km,两车同向而行,动车在货车后面,问动车开出后多少小时追上货车?
解方程,得
解:动车开出后x小时追上货车.根据题意,得
答:动车开出 h后追上货车.
等量关系: 360km + 货车行驶的路程 = 动车行驶的路程
等积变形和行程问题
列方程解应用题的一般步骤:
基本思路:
审题
设未知数
列方程
解方程
检验并写出答案
关键:弄清题意,找出相等关系.
实际
问题
一元一次
方程
一元一次
方程的解
实际问题的答案
解方程
检验解是否符合题意
抽象出
数学模型
教科书
第94页 练习
第1、2、3题
再见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
