人教版数学八年级上册 第十五章第50课时 分 式 方 程(一)课件 (共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十五章第50课时 分 式 方 程(一)课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 12:03:26 | ||
图片预览






文档简介
(共19张PPT)
第十五章分式
第50课时 分 式 方 程(一)
目录
01
本课目标
02
课堂导练
1.了解分式方程的概念,能判断一个方程是不是分式方程.
2.掌握分式方程的解法,会解可化为一元一次方程的分式方程,并会检验一个数是不是原方程的增根.
本课目标
知识重点
知识点一:分式方程的概念
分母中含未知数的方程叫做_____________.
分式方程
对点范例
D
知识点二:分式方程的解法
解分式方程的基本思路是将分式方程化为___________,具体做法是“去分母”,即方程两边乘_________________,这也是解分式方程的一般方法.最后要将整式方程的解代入最简公分母,若最简公分母的值不为0,则整式方程的解就是原分式方程的解;否则,这个解不是原分式方程的解.
知识重点
整式方程
最简公分母
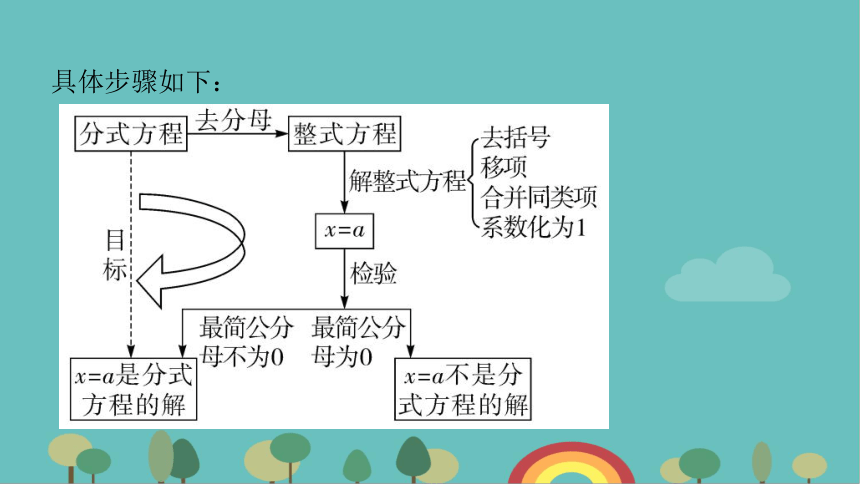
具体步骤如下:
对点范例
x(x+1)
2x=x+1
x=1
1
x(x+1)≠0
x=1
课堂导练
典型例题
②
举一反三
①②③
典型例题
解:方程两边乘(x-2),得
x-3+x-2=-3.
解得x=1.
检验:当x=1时,x-2≠0.
∴原分式方程的解为x=1.
思路点拨:解分式方程时,首先找出分式方程的最简公分母,去分母得到整式方程再求解,最后记得一定要验根.
解:方程两边乘x(x+1),得
2x-4(x+1)=0.
解得x=-2.
检验:当x=-2时,x(x+1)≠0.
∴原分式方程的解为x=-2.
举一反三
解:方程两边乘(2x-1),得
x-5=2(2x-1).
解得x=-1 .
检验:当x=-1时,2x-1≠0 .
∴原分式方程的解为x=-1 .
解:方程两边乘(x+1)(x-1),得
3(x-1)=2(x+1).
解得x=5.
检验:当x=5时,(x+1)(x-1)≠0.
∴原分式方程的解为x=5.
典型例题
解:方程两边乘(x-4),得
1-(x-3)=x-4.
解得x=4.
检验:当x=4时,x-4=0.
因此x=4不是原分式方程的解.
∴原分式方程无解.
举一反三
解:方程两边乘(x-2),得
x-1=1+3(x-2).
解得x=2.
检验:当x=2时,x-2=0.
因此x=2不是原分式方程的解.
∴原分式方程无解.
典型例题
举一反三
谢 谢
第十五章分式
第50课时 分 式 方 程(一)
目录
01
本课目标
02
课堂导练
1.了解分式方程的概念,能判断一个方程是不是分式方程.
2.掌握分式方程的解法,会解可化为一元一次方程的分式方程,并会检验一个数是不是原方程的增根.
本课目标
知识重点
知识点一:分式方程的概念
分母中含未知数的方程叫做_____________.
分式方程
对点范例
D
知识点二:分式方程的解法
解分式方程的基本思路是将分式方程化为___________,具体做法是“去分母”,即方程两边乘_________________,这也是解分式方程的一般方法.最后要将整式方程的解代入最简公分母,若最简公分母的值不为0,则整式方程的解就是原分式方程的解;否则,这个解不是原分式方程的解.
知识重点
整式方程
最简公分母
具体步骤如下:
对点范例
x(x+1)
2x=x+1
x=1
1
x(x+1)≠0
x=1
课堂导练
典型例题
②
举一反三
①②③
典型例题
解:方程两边乘(x-2),得
x-3+x-2=-3.
解得x=1.
检验:当x=1时,x-2≠0.
∴原分式方程的解为x=1.
思路点拨:解分式方程时,首先找出分式方程的最简公分母,去分母得到整式方程再求解,最后记得一定要验根.
解:方程两边乘x(x+1),得
2x-4(x+1)=0.
解得x=-2.
检验:当x=-2时,x(x+1)≠0.
∴原分式方程的解为x=-2.
举一反三
解:方程两边乘(2x-1),得
x-5=2(2x-1).
解得x=-1 .
检验:当x=-1时,2x-1≠0 .
∴原分式方程的解为x=-1 .
解:方程两边乘(x+1)(x-1),得
3(x-1)=2(x+1).
解得x=5.
检验:当x=5时,(x+1)(x-1)≠0.
∴原分式方程的解为x=5.
典型例题
解:方程两边乘(x-4),得
1-(x-3)=x-4.
解得x=4.
检验:当x=4时,x-4=0.
因此x=4不是原分式方程的解.
∴原分式方程无解.
举一反三
解:方程两边乘(x-2),得
x-1=1+3(x-2).
解得x=2.
检验:当x=2时,x-2=0.
因此x=2不是原分式方程的解.
∴原分式方程无解.
典型例题
举一反三
谢 谢
