23.2.3 关于原点对称的点的坐标 同步练习(含答案)
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 11:43:27 | ||
图片预览

文档简介
23.2.3 关于原点对称的点的坐标
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
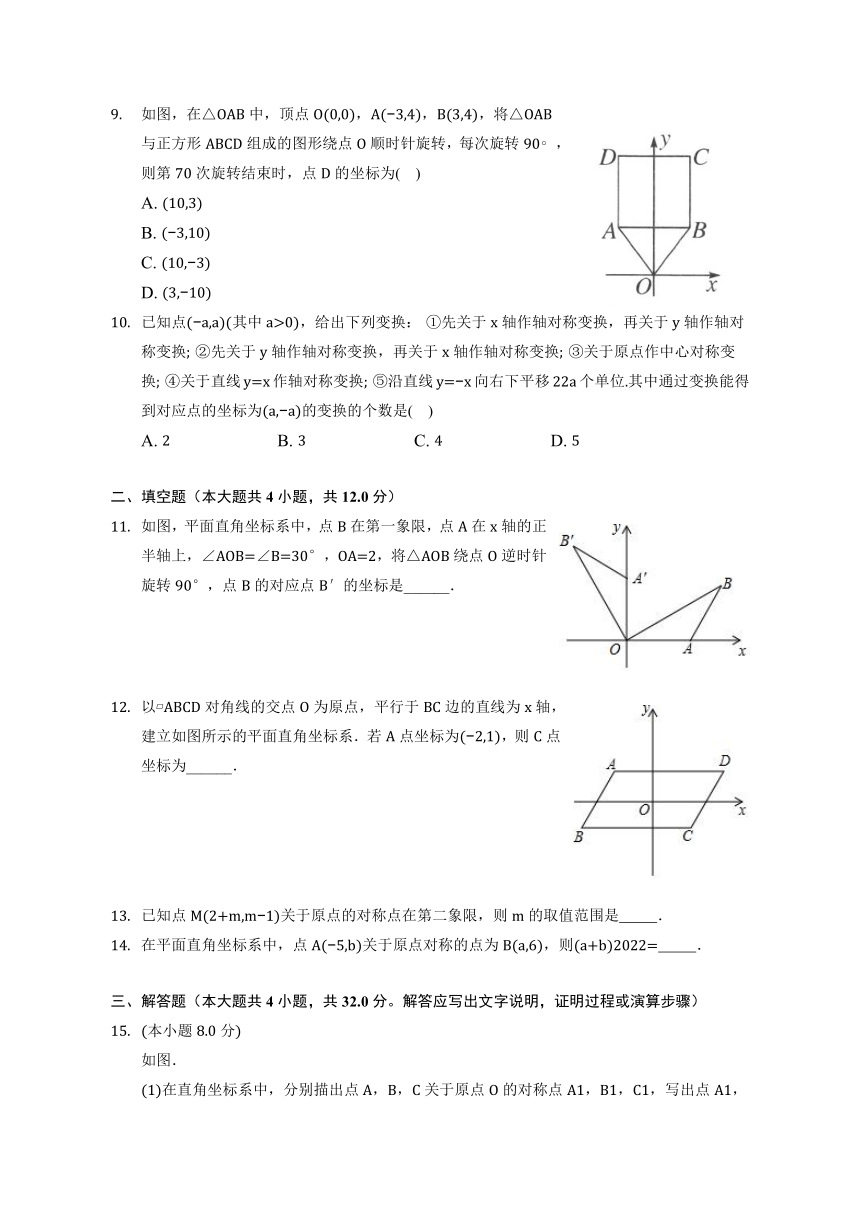
在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A. (2,3) B. ( 3,2) C. ( 3, 2) D. ( 2, 3)
如果点P1(a,3)和P2( 4,b)关于原点对称,则a+b的值为( )
A. 1 B. 1 C. 7 D. 7
在平面直角坐标系xOy中,△ABC与△A′B′C′关于原点O成中心对称的是( )
A. B.
C. D.
平面直角坐标系内与点P(3,4)关于原点对称的点的坐标是( )
A. ( 3,4) B. ( 3, 4) C. (3, 4) D. (4,3)
已知点A(x 2,3)与点B(x+4,y 5)关于原点对称,则( )
A. x= 1,y=2 B. x= 1,y=8
C. x= 1,y= 2 D. x=1,y=8
在平面直角坐标系中,点( 2,3)关于原点对称的点是( )
A. (3, 2) B. ( 2, 3) C. (2,3) D. (2, 3)
点P((π 3.14)0, ( 4)2)关于原点对称的点的坐标为( )
A. ( 1, 4) B. (1,4) C. ( 1,4) D. (1, 4)
若点P(2 m,5)关于原点对称的点是P′(3,2n+1),则m n的值为( )
A. 6 B. 3 C. 8 D. 9
如图,在△OAB中,顶点O(0,0),A( 3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90 ,则第70次旋转结束时,点D的坐标为( )
A. (10,3)
B. ( 3,10)
C. (10, 3)
D. (3, 10)
已知点( a,a)(其中a>0),给出下列变换: ①先关于x轴作轴对称变换,再关于y轴作轴对称变换; ②先关于y轴作轴对称变换,再关于x轴作轴对称变换; ③关于原点作中心对称变换; ④关于直线y=x作轴对称变换; ⑤沿直线y= x向右下平移22a个单位.其中通过变换能得到对应点的坐标为(a, a)的变换的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空题(本大题共4小题,共12.0分)
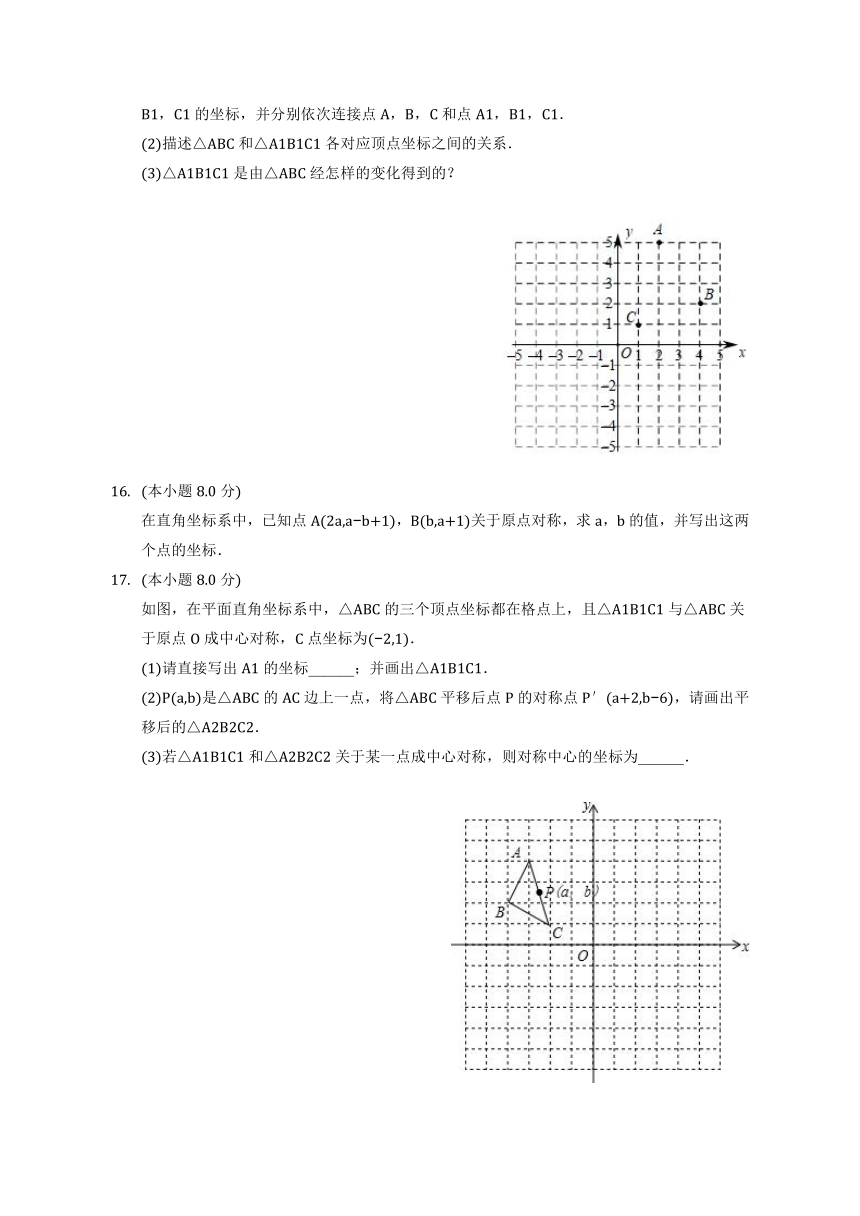
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是______.
以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为( 2,1),则C点坐标为______.
已知点M(2+m,m 1)关于原点的对称点在第二象限,则m的取值范围是 .
在平面直角坐标系中,点A( 5,b)关于原点对称的点为B(a,6),则(a+b)2022= .
三、解答题(本大题共4小题,共32.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题8.0分)
如图.
(1)在直角坐标系中,分别描出点A,B,C关于原点O的对称点A1,B1,C1,写出点A1,B1,C1的坐标,并分别依次连接点A,B,C和点A1,B1,C1.
(2)描述△ABC和△A1B1C1各对应顶点坐标之间的关系.
(3)△A1B1C1是由△ABC经怎样的变化得到的?
(本小题8.0分)
在直角坐标系中,已知点A(2a,a b+1),B(b,a+1)关于原点对称,求a,b的值,并写出这两个点的坐标.
(本小题8.0分)
如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为( 2,1).
(1)请直接写出A1的坐标______;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P′(a+2,b 6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为______.
(本小题8.0分)
如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】( 3,3)
12.【答案】(2, 1)
13.【答案】 214.【答案】1
15.【答案】解:(1)如图所示:
(2)△ABC和△A1B1C1各对应顶点的横坐标互为相反数,纵坐标互为相反数;
(3)△A1B1C1是由△ABC绕着原点O旋转180°得到的.
16.【答案】解:由点A(2a,a b+1),B(b,a+1)关于原点对称,得
2a+b=0a b+1+a+1=0,
解得a= 12b=1,
点A( 1, 12),B(1,12).
17.【答案】解:(1)(3, 4),如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)(1, 3)
18.【答案】解:(1)根据对称中心的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4 2=2,
∴B,C的坐标分别是( 2,4),( 2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上所述,可得顶点B,C,B1, C1的坐标分别是( 2,4),( 2,2),(2,1),(2,3).
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A. (2,3) B. ( 3,2) C. ( 3, 2) D. ( 2, 3)
如果点P1(a,3)和P2( 4,b)关于原点对称,则a+b的值为( )
A. 1 B. 1 C. 7 D. 7
在平面直角坐标系xOy中,△ABC与△A′B′C′关于原点O成中心对称的是( )
A. B.
C. D.
平面直角坐标系内与点P(3,4)关于原点对称的点的坐标是( )
A. ( 3,4) B. ( 3, 4) C. (3, 4) D. (4,3)
已知点A(x 2,3)与点B(x+4,y 5)关于原点对称,则( )
A. x= 1,y=2 B. x= 1,y=8
C. x= 1,y= 2 D. x=1,y=8
在平面直角坐标系中,点( 2,3)关于原点对称的点是( )
A. (3, 2) B. ( 2, 3) C. (2,3) D. (2, 3)
点P((π 3.14)0, ( 4)2)关于原点对称的点的坐标为( )
A. ( 1, 4) B. (1,4) C. ( 1,4) D. (1, 4)
若点P(2 m,5)关于原点对称的点是P′(3,2n+1),则m n的值为( )
A. 6 B. 3 C. 8 D. 9
如图,在△OAB中,顶点O(0,0),A( 3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90 ,则第70次旋转结束时,点D的坐标为( )
A. (10,3)
B. ( 3,10)
C. (10, 3)
D. (3, 10)
已知点( a,a)(其中a>0),给出下列变换: ①先关于x轴作轴对称变换,再关于y轴作轴对称变换; ②先关于y轴作轴对称变换,再关于x轴作轴对称变换; ③关于原点作中心对称变换; ④关于直线y=x作轴对称变换; ⑤沿直线y= x向右下平移22a个单位.其中通过变换能得到对应点的坐标为(a, a)的变换的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空题(本大题共4小题,共12.0分)
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是______.
以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为( 2,1),则C点坐标为______.
已知点M(2+m,m 1)关于原点的对称点在第二象限,则m的取值范围是 .
在平面直角坐标系中,点A( 5,b)关于原点对称的点为B(a,6),则(a+b)2022= .
三、解答题(本大题共4小题,共32.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题8.0分)
如图.
(1)在直角坐标系中,分别描出点A,B,C关于原点O的对称点A1,B1,C1,写出点A1,B1,C1的坐标,并分别依次连接点A,B,C和点A1,B1,C1.
(2)描述△ABC和△A1B1C1各对应顶点坐标之间的关系.
(3)△A1B1C1是由△ABC经怎样的变化得到的?
(本小题8.0分)
在直角坐标系中,已知点A(2a,a b+1),B(b,a+1)关于原点对称,求a,b的值,并写出这两个点的坐标.
(本小题8.0分)
如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为( 2,1).
(1)请直接写出A1的坐标______;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P′(a+2,b 6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为______.
(本小题8.0分)
如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】( 3,3)
12.【答案】(2, 1)
13.【答案】 2
15.【答案】解:(1)如图所示:
(2)△ABC和△A1B1C1各对应顶点的横坐标互为相反数,纵坐标互为相反数;
(3)△A1B1C1是由△ABC绕着原点O旋转180°得到的.
16.【答案】解:由点A(2a,a b+1),B(b,a+1)关于原点对称,得
2a+b=0a b+1+a+1=0,
解得a= 12b=1,
点A( 1, 12),B(1,12).
17.【答案】解:(1)(3, 4),如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)(1, 3)
18.【答案】解:(1)根据对称中心的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4 2=2,
∴B,C的坐标分别是( 2,4),( 2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上所述,可得顶点B,C,B1, C1的坐标分别是( 2,4),( 2,2),(2,1),(2,3).
同课章节目录
