5.2反比例函数的图象与性质(1)[上学期]
文档属性
| 名称 | 5.2反比例函数的图象与性质(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-12 06:48:00 | ||
图片预览





文档简介
课件14张PPT。反比例函数的图象和性质(1)复习提问1. 下列函数中哪些是反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1y = 2x2y = 3x2. 上节课我们学的反比例函数解析式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)1. 我们已研究过正比例函数,一次函
数的图像,那反比例函数的图像是否象
前面所学的函数一样是直线呢?
设问: 2. 图像会与坐标轴相交吗,为什么?
(不相交,x≠0 ,y≠0)反比例函数的图象和性质本节目标:1.进一步熟悉作函数图象的步骤,会作反比例
函数的图象。
2.体会函数的三种表示方法的相互转化,对函
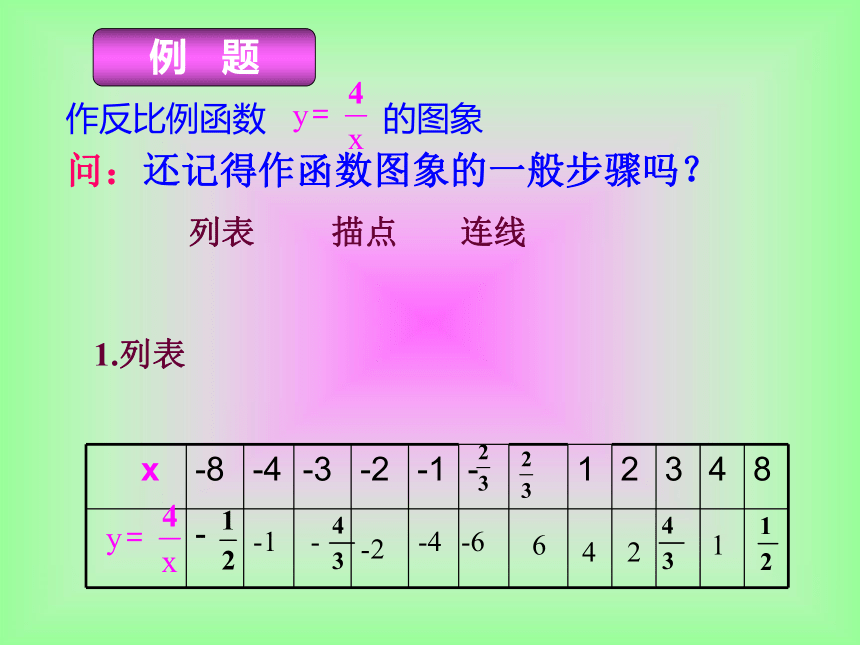
数进行认识上的整合.作反比例函数 的图象问:还记得作函数图象的一般步骤吗?
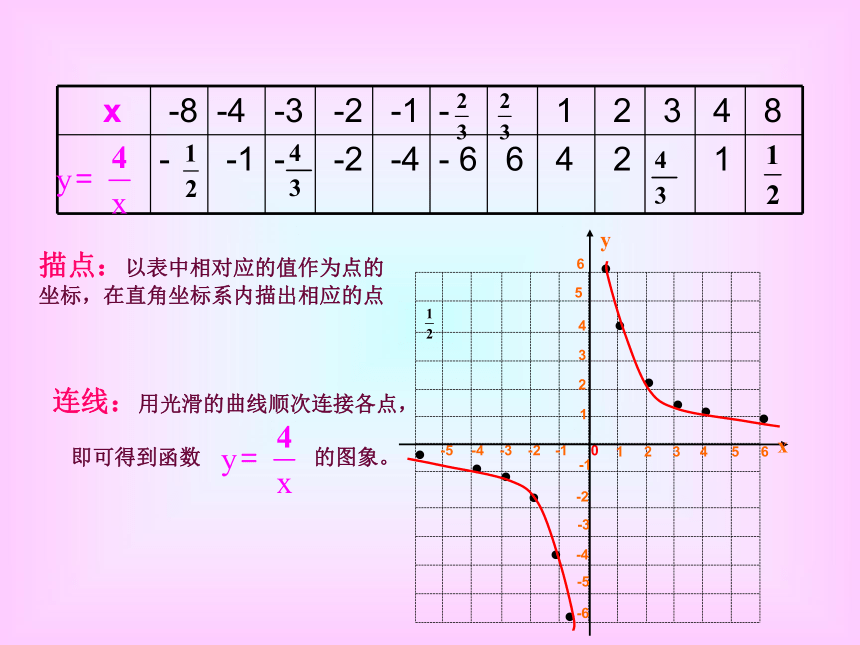
连线列表描点1.列表-1--2-4-64216例 题描点:以表中相对应的值作为点的坐标,在直角坐标系内描出相应的点连线:用光滑的曲线顺次连接各点,
即可得到函数 的图象。123456-1-3-2-4-51234-1-2-3-40-6-556xy............ 议一议:你认为作反比例函数图象时应该注意
哪些问题?
与同伴进行交流。 列表时,自变量的值可以选取绝对值相等而符号相反的
一对一对的值,这样既可简化计算,又便于描点; 列表、描点时,要尽量多取一些数值,多描出一些点,
这样方便连线。 连线必须是光滑的曲线。图象越来越靠近坐标轴,但与坐标轴不相交。 做一做:
作反比例函数 的图象123456-1-3-2-4-51234-1-2-3-40-6-556xy-- 讨论:
1. 如果列表时所取的数值不同,那么
图象的形状是否相同?
2. 函数 和 的图象
的两个分支 能经过旋转或平移相互得到吗?-(两个图象自身都是轴对称图形,关于原点中
心对称。)K<0K<0K>0K>0x取不为0的
所有实数 y=kx(k≠0)
x取一切实数你学到了什么?回顾本节:作反比例函数的图象 列表时,自变量的值可以选取绝对值相等而符号相反的
一对一对的值,这样既可简化计算,又便于描点; 列表、描点时,要尽量多取一些数值,多描出一些点,
这样方便连线。 连线必须是光滑的曲线。图象越来越靠近坐标轴,但与坐标轴不相交。反比例函数的图象反比例函数 的图象是由两支曲线组成的。
当 K>0 时,两支曲线分别位于第一、三象限内,当 K<0 时,两支曲线分别位于第二、四象限内。二,四m < 2一、三3一、三
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1y = 2x2y = 3x2. 上节课我们学的反比例函数解析式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)1. 我们已研究过正比例函数,一次函
数的图像,那反比例函数的图像是否象
前面所学的函数一样是直线呢?
设问: 2. 图像会与坐标轴相交吗,为什么?
(不相交,x≠0 ,y≠0)反比例函数的图象和性质本节目标:1.进一步熟悉作函数图象的步骤,会作反比例
函数的图象。
2.体会函数的三种表示方法的相互转化,对函
数进行认识上的整合.作反比例函数 的图象问:还记得作函数图象的一般步骤吗?
连线列表描点1.列表-1--2-4-64216例 题描点:以表中相对应的值作为点的坐标,在直角坐标系内描出相应的点连线:用光滑的曲线顺次连接各点,
即可得到函数 的图象。123456-1-3-2-4-51234-1-2-3-40-6-556xy............ 议一议:你认为作反比例函数图象时应该注意
哪些问题?
与同伴进行交流。 列表时,自变量的值可以选取绝对值相等而符号相反的
一对一对的值,这样既可简化计算,又便于描点; 列表、描点时,要尽量多取一些数值,多描出一些点,
这样方便连线。 连线必须是光滑的曲线。图象越来越靠近坐标轴,但与坐标轴不相交。 做一做:
作反比例函数 的图象123456-1-3-2-4-51234-1-2-3-40-6-556xy-- 讨论:
1. 如果列表时所取的数值不同,那么
图象的形状是否相同?
2. 函数 和 的图象
的两个分支 能经过旋转或平移相互得到吗?-(两个图象自身都是轴对称图形,关于原点中
心对称。)K<0K<0K>0K>0x取不为0的
所有实数 y=kx(k≠0)
x取一切实数你学到了什么?回顾本节:作反比例函数的图象 列表时,自变量的值可以选取绝对值相等而符号相反的
一对一对的值,这样既可简化计算,又便于描点; 列表、描点时,要尽量多取一些数值,多描出一些点,
这样方便连线。 连线必须是光滑的曲线。图象越来越靠近坐标轴,但与坐标轴不相交。反比例函数的图象反比例函数 的图象是由两支曲线组成的。
当 K>0 时,两支曲线分别位于第一、三象限内,当 K<0 时,两支曲线分别位于第二、四象限内。二,四m < 2一、三3一、三
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
