反比例函数的图象与性质2[上学期]

课件21张PPT。决不要企图掩饰自己知识上的缺陷。
哪怕是用最大胆的猜度和假设作为
借口来掩饰。
——巴普洛甫反比例函数的图象与性质复习回顾画函数图象的一般步骤
反比例函数是一条双曲线，它
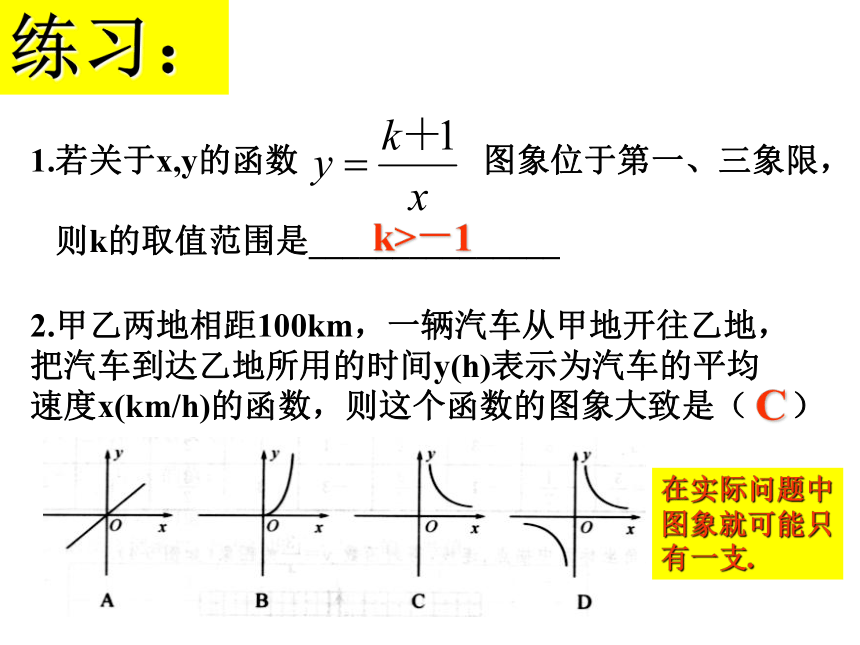
所在象限与k的关系怎样？列表 描点 连线练习：1.若关于x,y的函数 图象位于第一、三象限，
则k的取值范围是_______________k>－12.甲乙两地相距100km，一辆汽车从甲地开往乙地，
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数，则这个函数的图象大致是（ ）C在实际问题中
图象就可能只
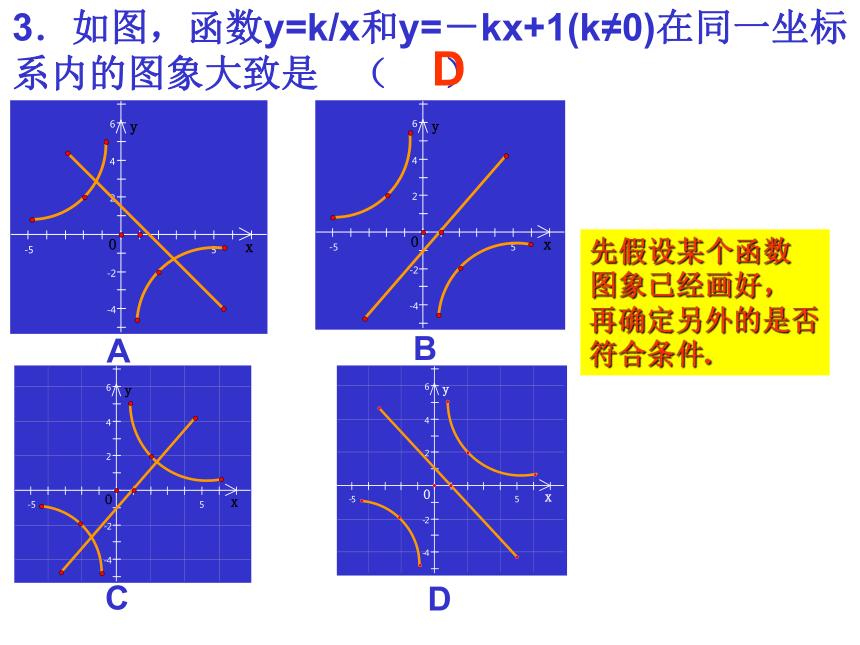
有一支.3．如图，函数y=k/x和y=－kx+1(k≠0)在同一坐标系内的图象大致是 （ ）BACDD先假设某个函数
图象已经画好，
再确定另外的是否
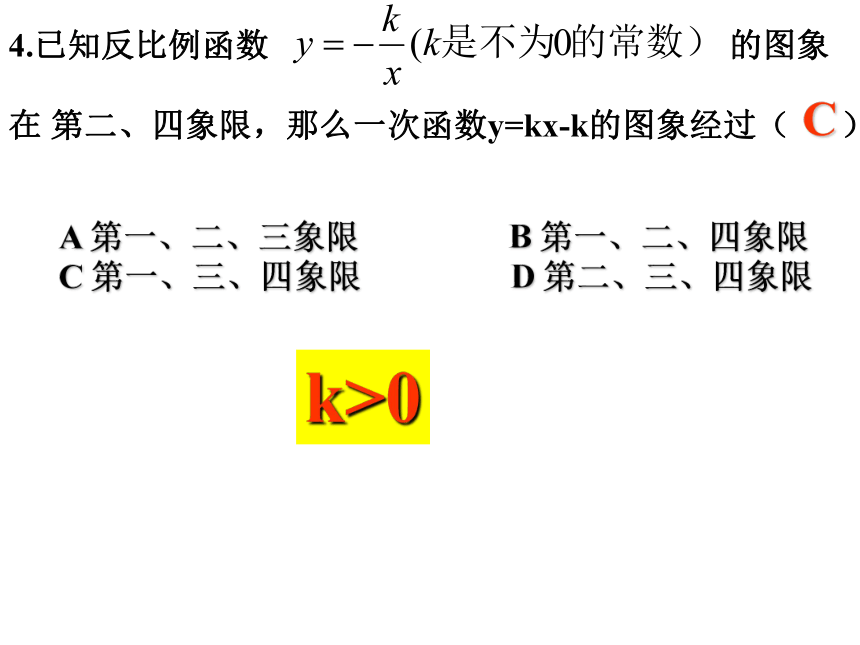
符合条件.4.已知反比例函数 的图象
在 第二、四象限，那么一次函数y=kx-k的图象经过（ ）A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限Ck>05.已知点（－m,n）在反比例函数的图象上，则
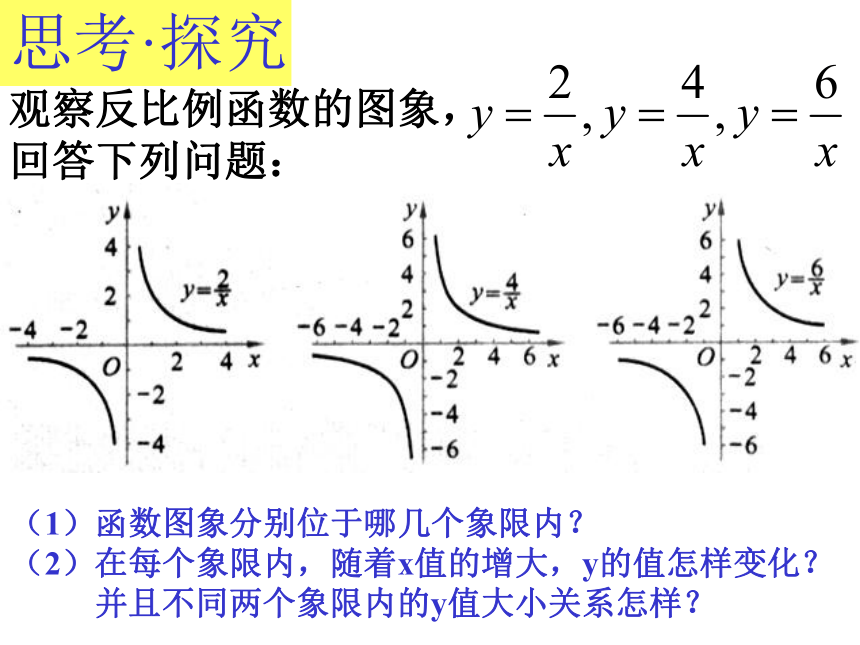
它的图象也一定经过点__________(m, －n)思考·探究观察反比例函数的图象，
回答下列问题：（1）函数图象分别位于哪几个象限内？
（2）在每个象限内，随着x值的增大，y的值怎样变化？
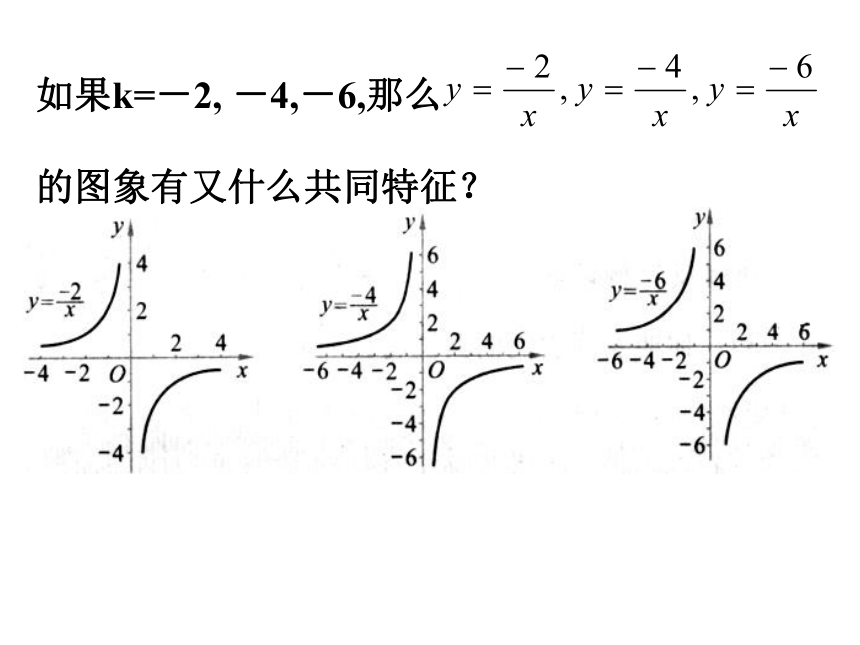
并且不同两个象限内的y值大小关系怎样？如果k=－2, －4,－6,那么
的图象有又什么共同特征？重要结论反比例函数的图象，当k>0时，在每一象限内，
y的值随x值的增大而减小，并且第一象限内的
y值大于第三象限内的y值；当k<0时，在每一
象限内，y的值随x值的增大而增大，并且第二
象限内的y值大于第四象限内的y值.例1 函数 的图象上有三点
（－3,y1）, （－1,y2）, （2,y3）,则函数值y1、y2、y3的
大小关系是_______________;y3< y1< y2例2 已知反比例函数 ,y随x的
增大而减小，求a的值和表达式.PQS1S2S1、S2有什么关系？为什么？反比例函数应用迁移,巩固提高考点一:反比例函数的性质.例1:（1）在一个反比例函数图象上任取两点P、Q，过点P分别作x轴、y轴的平行线，与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S2，S1与S2 有什么关系？（2）将反比例函数的图象绕原点旋转180°后，能与原来的图形重合吗？KQ（x2,y2）HONP（x1,y1）Mxy(k ≠0)应用迁移,巩固提高考点一:反比例函数的性质.例1:（1）在一个反比例函数图象上任取两点P、Q，过点P分别作x轴、y轴的平行线，与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S2，S1与S2 有什么关系？（2）将反比例函数的图象绕原点旋转180°后，能与原来的图形重合吗？KQ（x2,y2）HONP（x1,y1）Mxy(k ≠0)解:(2)能,反比例函数的图象是一个关于原点为中心的中心对称图形.注意:同时反比例函数的图象也是关于y=x和关于y= - x的轴对称图形.应用迁移,巩固提高考点二:反比例函数与一次函数的综合运用.解:∵∴∴∵∴∴
应用迁移,巩固提高考点二:反比例函数与一次函数的综合运用.例3.请在同一坐标系中,画出y=ax+b与 (其中ab≠0)的可能的大致图象.应用迁移,巩固提高考点二:反比例函数与一次函数的综合运用.例4.(2004贵阳)如图,一次函数y=ax+b的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于
一次函数的值的x的取值范围.应用迁移,巩固提高考点二:反比例函数与一次函数的综合运用.例4.(2004贵阳)如图,一次函数y=ax+b的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于
一次函数的值的x的取值范围.解:∴一次函数是y=2x-2(2)由图象可知:
当x<-1,或0要使两个函数的图象有两个不同的交点,必须使方程x2+6x+k=0有两个不相等的实数根,∴△=62 - 4k>0,解得k<9又k≠0∴当k<9且k≠0时,这两个函数的图象有两个不同的交点.总结与反思一.总结:
1.本节学习的数学知识:
(1)_____________________________,
(2)______________________________________________.反比例函数的图象与性质能将一次函数与反比例函数的图象与性质综合运用2.本节学习的数学方法:____________________________.数形结合,待定系数法二.反思:
反比例函数 (k≠0) 中的比例系数k有什么几何意义?