人教版七年级数学下册5.2 平行线及其判定 习题卷(含答案)
文档属性
| 名称 | 人教版七年级数学下册5.2 平行线及其判定 习题卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 00:00:00 | ||
图片预览


文档简介
5.2 平行线及其判定(习题卷)-2022年人教新版数学七年级下册
选择题
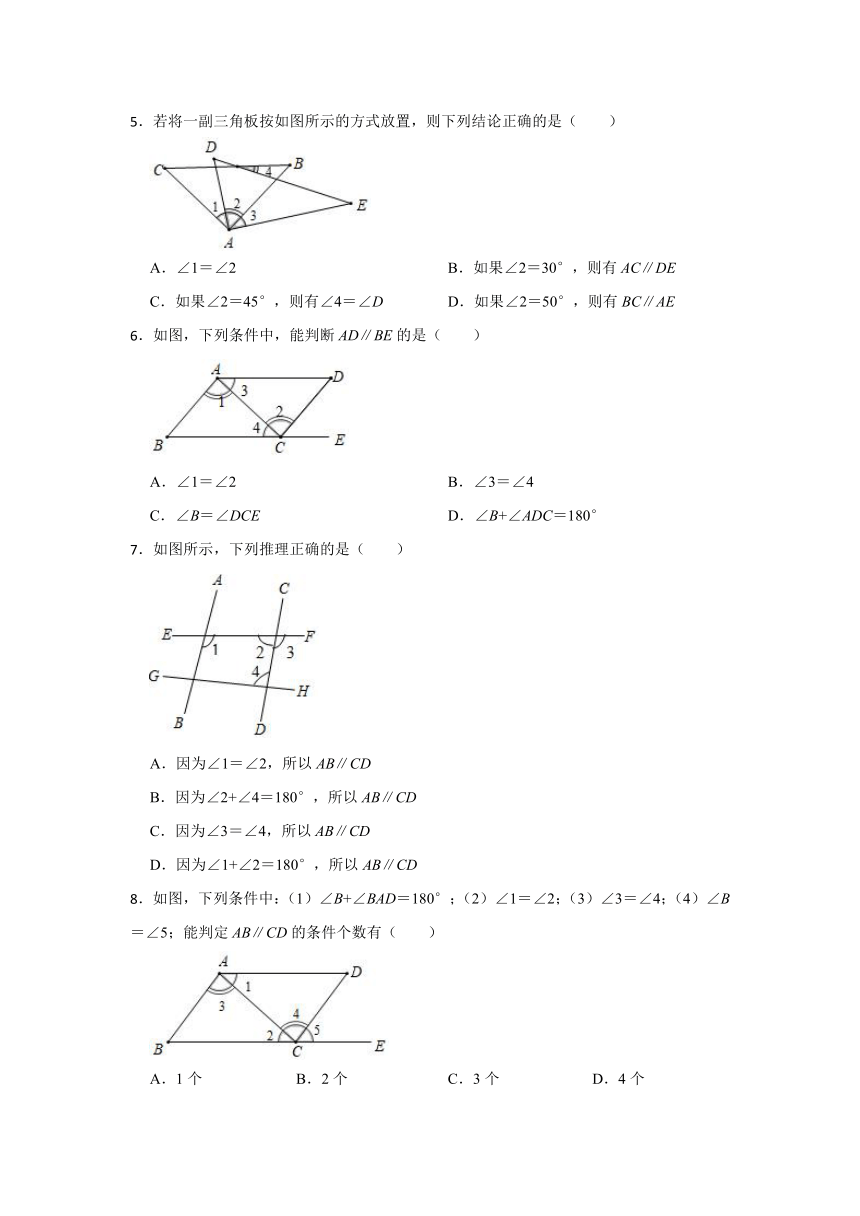
.如图,已知∠1=40°,∠B=50°,AB⊥AC,下列结论正确的是( )
A.AC⊥CD B.AB∥CD C.∠D=50° D.AD∥BC
.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1+∠2=90°
.如图,直线AB、CD被EF所截,∠1=135°,若要使AB∥CD,那么∠2的度数应为( )
A.150° B.45° C.135° D.180°
.如图,已知:∠1=∠2,∠3=∠4,那么下列结论成立的是( )
A.∠1=∠3 B.∠2=∠3 C.AB∥CD D.AE∥DF
.若将一副三角板按如图所示的方式放置,则下列结论正确的是( )
A.∠1=∠2 B.如果∠2=30°,则有AC∥DE
C.如果∠2=45°,则有∠4=∠D D.如果∠2=50°,则有BC∥AE
.如图,下列条件中,能判断AD∥BE的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠B+∠ADC=180°
.如图所示,下列推理正确的是( )
A.因为∠1=∠2,所以AB∥CD
B.因为∠2+∠4=180°,所以AB∥CD
C.因为∠3=∠4,所以AB∥CD
D.因为∠1+∠2=180°,所以AB∥CD
.如图,下列条件中:(1)∠B+∠BAD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5;能判定AB∥CD的条件个数有( )
A.1个 B.2个 C.3个 D.4个
.下面说法正确的个数为( )
(1)在同一平面内,过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
.如图,AC、BD相交于点O,连接AB、BC、CD、DA,能判定AD∥BC的条件是( )
A.∠CDB=∠ABD B.∠ADC+∠DAB=180°
C.∠DCA=∠BAC D.∠DAC=∠BCA
填空题
.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,
改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 .
.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2; ②∠3=∠6;③∠1=∠4;④∠5+∠8=180°,其中能判断a∥b的条件是: .(把你认为正确的序号填在空格内)
.如图所示,请写出一个能判定l1∥l2的条件: .
.如图,能判断AD∥BC的条件是 (写出一个正确的就可以).
.下列说法中:
①棱柱的上、下底面的形状相同;
②若AB=BC,则点B为线段AC的中点;
③相等的两个角一定是对顶角;
④在同一平面内,不相交的两条直线叫做平行线;
⑤直线外一点与直线上各点连接的所有线段中,垂线段最短.正确的有 .(只填序号)
三.解答题
.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
.先填空,再完成证明.
证明:平行于同一条直线的两条直线平行.
已知:如图,直线a、b、c中, .
求证: .
证明: .
.将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).
.阅读下面材料
[材料一]异面直线
(1)定义:不同在任何一个平面内的两直线叫做异面直线.
(2)特点:既不相交,也不平行.
(3)理解:
①“不同在任何一个平面内”,指这两条直线不具备确定平面的条件,因此,异面直线既不相交,也不平行,要注意把握异面直线的不共面性.
②“不同在任……”也可以理解为“任何一个平面都不可能同时经过这两条直线”.
③不能把异面直线误解为分别在不同平面内的两条直线为异面直线.也就是说,在两个不同平面内的直线,它们既可以是平行直线,也可以是相交直线.
例如:如图,在长方体ABCD﹣A1B1C1D1中,棱A1D1所在直线与棱AB所在直线是异面直线,棱A1D1所在直线与棱BC所在直线就不是异面直线.
[材料二]在七年级下册第五章有这样一段话:“由平行公理,进一步可以得到如下结论:
如果两条直线都与第三条直线平行,那么这两条直线也平行.
其实,这个结论不仅在平面内成立,在空间内仍然成立.
利用材料中的信息,解答下列问题
(1)如图,在长方体ABCD﹣A1B1C1D1中,与棱A1A所在直线成异面直线的是
A.棱A1D1所在直线 B.棱B1C1所在直线
C.棱C1C所在直线 D.棱B1B 所在直线
(2)在空间内,两条直线的位置关系有 、 、 .(重合除外)
(3)如图,在长方体ABCD﹣A1B1C1D1中,已知E,F分别为BC,AB的中点,求证:EF∥A1C1.
.如图1,已知AC∥BD,点P是直线AC,BD间的一点,连接AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
选择题
.如图,已知∠1=40°,∠B=50°,AB⊥AC,下列结论正确的是( )
A.AC⊥CD B.AB∥CD C.∠D=50° D.AD∥BC
.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1+∠2=90°
.如图,直线AB、CD被EF所截,∠1=135°,若要使AB∥CD,那么∠2的度数应为( )
A.150° B.45° C.135° D.180°
.如图,已知:∠1=∠2,∠3=∠4,那么下列结论成立的是( )
A.∠1=∠3 B.∠2=∠3 C.AB∥CD D.AE∥DF
.若将一副三角板按如图所示的方式放置,则下列结论正确的是( )
A.∠1=∠2 B.如果∠2=30°,则有AC∥DE
C.如果∠2=45°,则有∠4=∠D D.如果∠2=50°,则有BC∥AE
.如图,下列条件中,能判断AD∥BE的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠B+∠ADC=180°
.如图所示,下列推理正确的是( )
A.因为∠1=∠2,所以AB∥CD
B.因为∠2+∠4=180°,所以AB∥CD
C.因为∠3=∠4,所以AB∥CD
D.因为∠1+∠2=180°,所以AB∥CD
.如图,下列条件中:(1)∠B+∠BAD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5;能判定AB∥CD的条件个数有( )
A.1个 B.2个 C.3个 D.4个
.下面说法正确的个数为( )
(1)在同一平面内,过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
.如图,AC、BD相交于点O,连接AB、BC、CD、DA,能判定AD∥BC的条件是( )
A.∠CDB=∠ABD B.∠ADC+∠DAB=180°
C.∠DCA=∠BAC D.∠DAC=∠BCA
填空题
.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,
改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 .
.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2; ②∠3=∠6;③∠1=∠4;④∠5+∠8=180°,其中能判断a∥b的条件是: .(把你认为正确的序号填在空格内)
.如图所示,请写出一个能判定l1∥l2的条件: .
.如图,能判断AD∥BC的条件是 (写出一个正确的就可以).
.下列说法中:
①棱柱的上、下底面的形状相同;
②若AB=BC,则点B为线段AC的中点;
③相等的两个角一定是对顶角;
④在同一平面内,不相交的两条直线叫做平行线;
⑤直线外一点与直线上各点连接的所有线段中,垂线段最短.正确的有 .(只填序号)
三.解答题
.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
.先填空,再完成证明.
证明:平行于同一条直线的两条直线平行.
已知:如图,直线a、b、c中, .
求证: .
证明: .
.将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).
.阅读下面材料
[材料一]异面直线
(1)定义:不同在任何一个平面内的两直线叫做异面直线.
(2)特点:既不相交,也不平行.
(3)理解:
①“不同在任何一个平面内”,指这两条直线不具备确定平面的条件,因此,异面直线既不相交,也不平行,要注意把握异面直线的不共面性.
②“不同在任……”也可以理解为“任何一个平面都不可能同时经过这两条直线”.
③不能把异面直线误解为分别在不同平面内的两条直线为异面直线.也就是说,在两个不同平面内的直线,它们既可以是平行直线,也可以是相交直线.
例如:如图,在长方体ABCD﹣A1B1C1D1中,棱A1D1所在直线与棱AB所在直线是异面直线,棱A1D1所在直线与棱BC所在直线就不是异面直线.
[材料二]在七年级下册第五章有这样一段话:“由平行公理,进一步可以得到如下结论:
如果两条直线都与第三条直线平行,那么这两条直线也平行.
其实,这个结论不仅在平面内成立,在空间内仍然成立.
利用材料中的信息,解答下列问题
(1)如图,在长方体ABCD﹣A1B1C1D1中,与棱A1A所在直线成异面直线的是
A.棱A1D1所在直线 B.棱B1C1所在直线
C.棱C1C所在直线 D.棱B1B 所在直线
(2)在空间内,两条直线的位置关系有 、 、 .(重合除外)
(3)如图,在长方体ABCD﹣A1B1C1D1中,已知E,F分别为BC,AB的中点,求证:EF∥A1C1.
.如图1,已知AC∥BD,点P是直线AC,BD间的一点,连接AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图2,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
