2022-2023学年 人教版九年级 数学上册22.3 实际问题与二次函数 销售问题 同步卷 (含答案)
文档属性
| 名称 | 2022-2023学年 人教版九年级 数学上册22.3 实际问题与二次函数 销售问题 同步卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 538.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 16:05:08 | ||
图片预览




文档简介
22.3 销售问题(实际问题与二次函数)同步卷
一、单选题
1.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
2.将进货单价为元的某种商品按零售价元一个售出时,每天能卖出个.若这种商品的零售价在一定范围内每降价元,其日销售量就增加个,则能获取的最大利润是( )
A.元 B.元 C.元 D.元
3.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
4.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
5.西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3 B.0.4 C.0.3 D.0.2
二、填空题
6.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
7.商场某种商品进价为120元/件,售价130元/件时,每天可销售70件;售价单价高于130元时,每涨价1元,日销售量就减少1件,据此,若销售单价为 __________元时,商场每天盈利达1500元.
三、解答题
8.商场某种商品平均每天可销售30件,每件赢利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多销售出2件.
(1)若某天,该商品每天降价4元,当天可获利多少元?
(2)每件商品降多少元,商场日利润可达2100元?
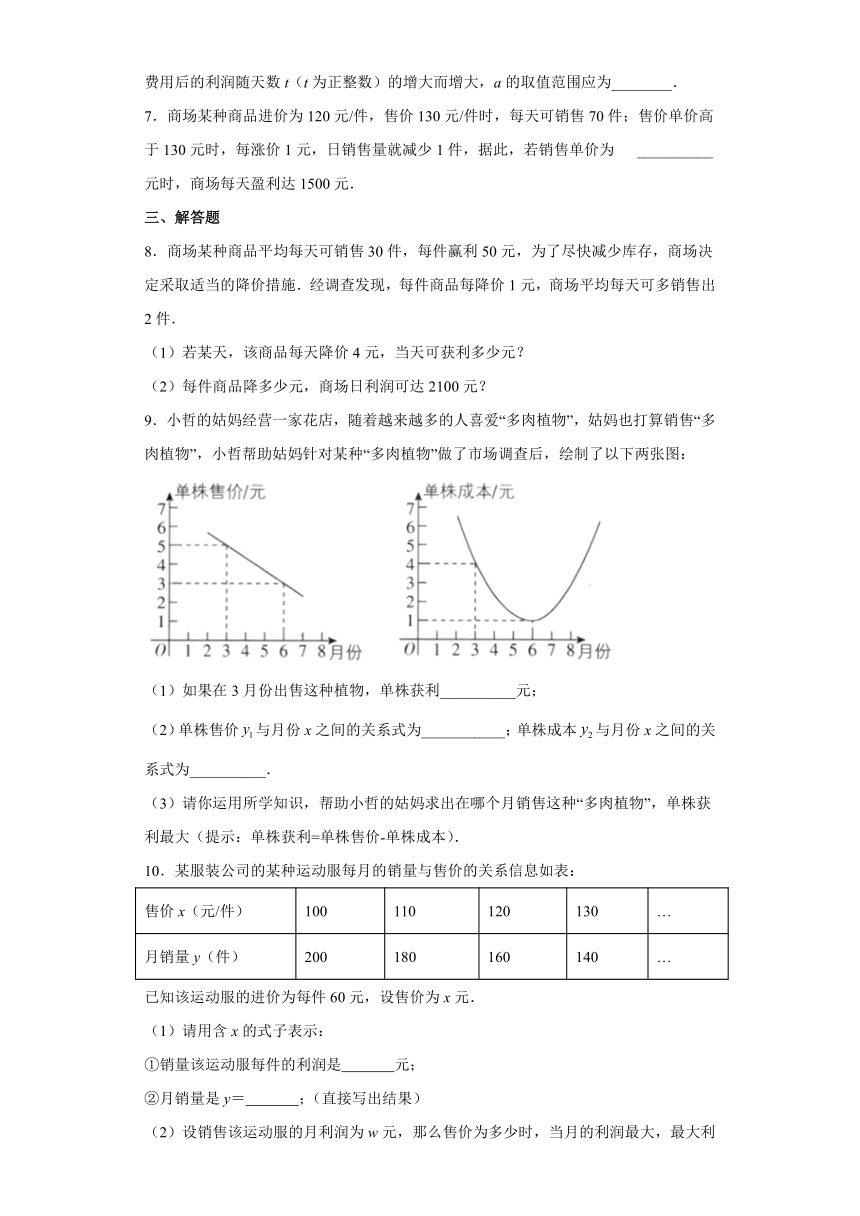
9.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图:
(1)如果在3月份出售这种植物,单株获利__________元;
(2)单株售价与月份x之间的关系式为___________;单株成本与月份x之间的关系式为__________.
(3)请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).
10.某服装公司的某种运动服每月的销量与售价的关系信息如表:
售价x(元/件) 100 110 120 130 …
月销量y(件) 200 180 160 140 …
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:
①销量该运动服每件的利润是 元;
②月销量是y= ;(直接写出结果)
(2)设销售该运动服的月利润为w元,那么售价为多少时,当月的利润最大,最大利润时多少?
(3)该公司决定每销售一件运动服,就捐赠a(a>0)元利润给希望工程,物价部门规定该运动服售价不得超过120元,设销售该运动服的月利润为w元,若月销售最大利润是8800元,求a的值.
11.2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,某市政府加大各部门和各单位的对口扶贫力度.某单位帮扶某村完成一种农产品的销售工作,其成本为每件10元,销售过程中发现,该产品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的一次函数关系.
(1)请求出y与x之间的函数解析式;
(2)该农产品的销售单价为多少元时,每天的销售利润最大?最大利润是多少元?
12.某超市以每次20元的价格新进一批商品,经市场调研发现该商品每天的销售量件与销售价格元件的关系如图所示.
(1)试确定y与x之间的函数表达式(写出自变量的取值范围);
(2)若超市一天销售该商品的利润为(元),写出W与商品的售价(元件)之间的函数表达式;
(3)在(2)的条件下,当销售价格x定为多少时,一天的利润W最大,最大利润是多少?
13.小月的妈妈经营一家装饰店,随着越来越多的人喜爱鲜花,小月的妈妈也打算销售鲜花.小月帮助妈妈针对某种鲜花做了市场调查后,绘制了以下两张图表:
(1)如果在六月份出售这种鲜花,单株获利 元;
(2)请你运用所学知识,求出在哪个月销售这种鲜花,单株获利最大,最大值为多少?(提示:单株获利=单株售价﹣单株成本)
14.汈汊湖素有鱼米之乡的美誉,某水产养殖大户为了更好地发挥技术优势,一次性收购了淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系为;y与t的函数关系如图所示.
(1)分别求出当和时,y与t的函数关系式;
(2)设将这批淡水鱼放养t天后一次性出售所得利润为w元,求当t为何值时,w最大?并求出最大值.(利润=销售总额-总成本)
1.C
【详解】解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
2.B
【详解】解:设降价元,所获得的利润为元,
则
,
,
当元时,二次函数有最大值.
获得的最大利润为625元.
故选:.
3.D
【详解】因为每降低5元,每天可多售出10件,所以每降价1元可多售2件,
设每件降价x元,每天的利润为y元,则每天可售(20+2x)件,每件利润为40-x,
所以每天的利润为
将整理成顶点式有,
由顶点式可知当销售单价降低15元时,每天获得利润最大,每天的最大利润为1250元,故A、B正确;
将x=10代入到解析式中解得y=1200,故C正确;
令y=1050,则,解得,即当每天的利润为1050元,则销售单价可能降低了5元,也可能降低了25元,所以D错误;
综上所述,答案选D.
4.B
【详解】解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得: 即y=(x-35)(400-5x),
故选:B.
5.C
【详解】设应将每千克小型西瓜的售价降低x元.那么每千克的利润为:(3﹣2﹣x),由于这种小型西瓜每降价O.1元/千克,每天可多售出40千克.所以降价x元,则每天售出数量为:200+千克.本题的等量关系为:每千克的利润×每天售出数量﹣固定成本=200.
解:设应将每千克小型西瓜的售价降低x元.
根据题意,得(3﹣2﹣x)(200+)﹣24=200.
解这个方程,得x1=0.2,x2=0.3.
∵200+>200+,
∴应将每千克小型西瓜的售价降低0.3元.
故选C.
6.0<a<6
【详解】试题解析:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)-(20+4t)a
化简,得
y=-4t2+(260-4a)t+1400-20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴
解得,a<6,
又∵a>0,
即a的取值范围是:0<a<6.
7.150或170 170或150
【详解】解:设涨价x元,根据题意得:(130+x-120)(70-x)=1500,
整理得:x2-60x+800=0,
解得:x1=20,x2=40,
所以销售单价为130+20=150元或130+40=170元,
故答案为:150或170.
8.(1)1748元;(2)20元.
【详解】解:(1)当天盈利:(50-4)×(30+2×4)=1748(元).
答:若某天该商品每件降价4元,当天可获利1748元.
(2)设每件商品降价x元,则商场日销售量增加2x件,每件商品,盈利(50-x)元.根据题意,得:
(50-x)×(30+2x)=2100,
整理,得:x2-35x+300=0,
解得:x1=15,x2=20,
∵商城要尽快减少库存,
∴x=20.
答:每件商品降价20元时,商场日盈利可达到2100元.
9.(1)1;(2);;(3)5月份销售这种“多肉植物”,单株获利最大.
【详解】(1)从题图知,3月份的单株售价为5元,单株成本为4元,
∴单株获利为(元).
故答案为1.
(2)设直线的关系式为.
把点代入上式得
解得
∴直线的关系式为.
设抛物线的关系式为.
把点代入上式得,
解得,
∴抛物线的关系式为.
故答案为;.
(3).
∵,
∴当时,取得最大值.
答:5月份销售这种“多肉植物”,单株获利最大.
10.(1)(x﹣60);﹣2x+400;(2)售价为130元时,当月的利润最大,最大利润是9800元;(3)a=5.
【详解】(1)①销售该运动服每件的利润是(x﹣60)元;
②设月销量y与x的关系式为y=kx+b,
由题意得,,
解得,,
∴y=﹣2x+400;
(2)由题意得,w=(x﹣60)(﹣2x+400)
=﹣2x2+520x﹣24000
=﹣2(x﹣130)2+9800,
∴售价为130元时,当月的利润最大,最大利润是9800元;
(3)根据题意得,w=(x﹣60﹣a)(﹣2x+400)=﹣2x2+(520+2a)x﹣24000﹣400a,
∵对称轴x=,
∴①当<120时(舍),②当≥120时,x=120时,w求最大值8800,
解得:a=5.
11.(1)y=﹣10x+300;(2)销售单价定为20元时,每天销售利润最大,最大销售利润为1000元
【详解】解:(1)设y与x的函数关系式为y=kx+b,将(20,100),(25,50)代入y=kx+b,
得,
解得:,
∴y与x的函数关系式为y=﹣10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元.
12.(1);
(2);
(3)当销售价格x定为45元时,一天的利润W最大,最大利润是6250元
【详解】解:分两种情况:当时,设,
根据题意,得,
,
解得
故;
当时,设,
根据题意,得,
解得,
;
故每天销售量件与售价元件之间的函数表达式是:
;
,
当时,,
由于,抛物线开口向上,又,
因此当时,;
当时,,
由于,抛物线开口向下,又,
所以当时,,
综上所述,当时,.
13.(1)2;(2)5月份销售这种鲜花,单株获利最大,最大值为元
【详解】解:(1)从左图看,6月份售价为3元,从右图看,6月份的成本为1元,
则每株获利为3﹣1=2(元),
故答案为:2;
(2)设直线的表达式为:y1=kx+b(k≠0),
把点(3,5)、(6,3)代入上式得:,
解得:,
∴直线的表达式为:y1=x+7;
设:抛物线的表达式为:y2=a(x﹣m)2+n,
∵顶点为(6,1),则函数表达式为:y2=a(x﹣6)2+1,
把点(3,4)代入上式得:
4=a(3﹣6)2+1,解得:a=,
则抛物线的表达式为:y2=(x﹣6)2+1,
∴y1﹣y2=x+7﹣(x﹣6)2﹣1=﹣(x﹣5)2+,
∵﹣<0,
∴x=5时,函数取得最大值,最大值为元,
故:5月份销售这种鲜花,单株获利最大,最大值为元.
14.(1)当和时,和;(2)当t为55天时,w最大,最大值为180250元.
【详解】(1)当时,设y与t的函数关系式为产.
依题意得:,解得:
与t的函数关系式为.
当时,设y与x的函数关系式为.
依题意得:,解得:
与t的函数关系式为.
当和时,
y与t的函数关系式分别为和.
(2)由题意得,当时,
,当时,(元)
当时,
,当时,
综上所述,当t为55天时,w最大,最大值为180250元.
一、单选题
1.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
2.将进货单价为元的某种商品按零售价元一个售出时,每天能卖出个.若这种商品的零售价在一定范围内每降价元,其日销售量就增加个,则能获取的最大利润是( )
A.元 B.元 C.元 D.元
3.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
4.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
5.西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3 B.0.4 C.0.3 D.0.2
二、填空题
6.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
7.商场某种商品进价为120元/件,售价130元/件时,每天可销售70件;售价单价高于130元时,每涨价1元,日销售量就减少1件,据此,若销售单价为 __________元时,商场每天盈利达1500元.
三、解答题
8.商场某种商品平均每天可销售30件,每件赢利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多销售出2件.
(1)若某天,该商品每天降价4元,当天可获利多少元?
(2)每件商品降多少元,商场日利润可达2100元?
9.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图:
(1)如果在3月份出售这种植物,单株获利__________元;
(2)单株售价与月份x之间的关系式为___________;单株成本与月份x之间的关系式为__________.
(3)请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).
10.某服装公司的某种运动服每月的销量与售价的关系信息如表:
售价x(元/件) 100 110 120 130 …
月销量y(件) 200 180 160 140 …
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:
①销量该运动服每件的利润是 元;
②月销量是y= ;(直接写出结果)
(2)设销售该运动服的月利润为w元,那么售价为多少时,当月的利润最大,最大利润时多少?
(3)该公司决定每销售一件运动服,就捐赠a(a>0)元利润给希望工程,物价部门规定该运动服售价不得超过120元,设销售该运动服的月利润为w元,若月销售最大利润是8800元,求a的值.
11.2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,某市政府加大各部门和各单位的对口扶贫力度.某单位帮扶某村完成一种农产品的销售工作,其成本为每件10元,销售过程中发现,该产品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的一次函数关系.
(1)请求出y与x之间的函数解析式;
(2)该农产品的销售单价为多少元时,每天的销售利润最大?最大利润是多少元?
12.某超市以每次20元的价格新进一批商品,经市场调研发现该商品每天的销售量件与销售价格元件的关系如图所示.
(1)试确定y与x之间的函数表达式(写出自变量的取值范围);
(2)若超市一天销售该商品的利润为(元),写出W与商品的售价(元件)之间的函数表达式;
(3)在(2)的条件下,当销售价格x定为多少时,一天的利润W最大,最大利润是多少?
13.小月的妈妈经营一家装饰店,随着越来越多的人喜爱鲜花,小月的妈妈也打算销售鲜花.小月帮助妈妈针对某种鲜花做了市场调查后,绘制了以下两张图表:
(1)如果在六月份出售这种鲜花,单株获利 元;
(2)请你运用所学知识,求出在哪个月销售这种鲜花,单株获利最大,最大值为多少?(提示:单株获利=单株售价﹣单株成本)
14.汈汊湖素有鱼米之乡的美誉,某水产养殖大户为了更好地发挥技术优势,一次性收购了淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系为;y与t的函数关系如图所示.
(1)分别求出当和时,y与t的函数关系式;
(2)设将这批淡水鱼放养t天后一次性出售所得利润为w元,求当t为何值时,w最大?并求出最大值.(利润=销售总额-总成本)
1.C
【详解】解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
2.B
【详解】解:设降价元,所获得的利润为元,
则
,
,
当元时,二次函数有最大值.
获得的最大利润为625元.
故选:.
3.D
【详解】因为每降低5元,每天可多售出10件,所以每降价1元可多售2件,
设每件降价x元,每天的利润为y元,则每天可售(20+2x)件,每件利润为40-x,
所以每天的利润为
将整理成顶点式有,
由顶点式可知当销售单价降低15元时,每天获得利润最大,每天的最大利润为1250元,故A、B正确;
将x=10代入到解析式中解得y=1200,故C正确;
令y=1050,则,解得,即当每天的利润为1050元,则销售单价可能降低了5元,也可能降低了25元,所以D错误;
综上所述,答案选D.
4.B
【详解】解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得: 即y=(x-35)(400-5x),
故选:B.
5.C
【详解】设应将每千克小型西瓜的售价降低x元.那么每千克的利润为:(3﹣2﹣x),由于这种小型西瓜每降价O.1元/千克,每天可多售出40千克.所以降价x元,则每天售出数量为:200+千克.本题的等量关系为:每千克的利润×每天售出数量﹣固定成本=200.
解:设应将每千克小型西瓜的售价降低x元.
根据题意,得(3﹣2﹣x)(200+)﹣24=200.
解这个方程,得x1=0.2,x2=0.3.
∵200+>200+,
∴应将每千克小型西瓜的售价降低0.3元.
故选C.
6.0<a<6
【详解】试题解析:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)-(20+4t)a
化简,得
y=-4t2+(260-4a)t+1400-20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴
解得,a<6,
又∵a>0,
即a的取值范围是:0<a<6.
7.150或170 170或150
【详解】解:设涨价x元,根据题意得:(130+x-120)(70-x)=1500,
整理得:x2-60x+800=0,
解得:x1=20,x2=40,
所以销售单价为130+20=150元或130+40=170元,
故答案为:150或170.
8.(1)1748元;(2)20元.
【详解】解:(1)当天盈利:(50-4)×(30+2×4)=1748(元).
答:若某天该商品每件降价4元,当天可获利1748元.
(2)设每件商品降价x元,则商场日销售量增加2x件,每件商品,盈利(50-x)元.根据题意,得:
(50-x)×(30+2x)=2100,
整理,得:x2-35x+300=0,
解得:x1=15,x2=20,
∵商城要尽快减少库存,
∴x=20.
答:每件商品降价20元时,商场日盈利可达到2100元.
9.(1)1;(2);;(3)5月份销售这种“多肉植物”,单株获利最大.
【详解】(1)从题图知,3月份的单株售价为5元,单株成本为4元,
∴单株获利为(元).
故答案为1.
(2)设直线的关系式为.
把点代入上式得
解得
∴直线的关系式为.
设抛物线的关系式为.
把点代入上式得,
解得,
∴抛物线的关系式为.
故答案为;.
(3).
∵,
∴当时,取得最大值.
答:5月份销售这种“多肉植物”,单株获利最大.
10.(1)(x﹣60);﹣2x+400;(2)售价为130元时,当月的利润最大,最大利润是9800元;(3)a=5.
【详解】(1)①销售该运动服每件的利润是(x﹣60)元;
②设月销量y与x的关系式为y=kx+b,
由题意得,,
解得,,
∴y=﹣2x+400;
(2)由题意得,w=(x﹣60)(﹣2x+400)
=﹣2x2+520x﹣24000
=﹣2(x﹣130)2+9800,
∴售价为130元时,当月的利润最大,最大利润是9800元;
(3)根据题意得,w=(x﹣60﹣a)(﹣2x+400)=﹣2x2+(520+2a)x﹣24000﹣400a,
∵对称轴x=,
∴①当<120时(舍),②当≥120时,x=120时,w求最大值8800,
解得:a=5.
11.(1)y=﹣10x+300;(2)销售单价定为20元时,每天销售利润最大,最大销售利润为1000元
【详解】解:(1)设y与x的函数关系式为y=kx+b,将(20,100),(25,50)代入y=kx+b,
得,
解得:,
∴y与x的函数关系式为y=﹣10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元.
12.(1);
(2);
(3)当销售价格x定为45元时,一天的利润W最大,最大利润是6250元
【详解】解:分两种情况:当时,设,
根据题意,得,
,
解得
故;
当时,设,
根据题意,得,
解得,
;
故每天销售量件与售价元件之间的函数表达式是:
;
,
当时,,
由于,抛物线开口向上,又,
因此当时,;
当时,,
由于,抛物线开口向下,又,
所以当时,,
综上所述,当时,.
13.(1)2;(2)5月份销售这种鲜花,单株获利最大,最大值为元
【详解】解:(1)从左图看,6月份售价为3元,从右图看,6月份的成本为1元,
则每株获利为3﹣1=2(元),
故答案为:2;
(2)设直线的表达式为:y1=kx+b(k≠0),
把点(3,5)、(6,3)代入上式得:,
解得:,
∴直线的表达式为:y1=x+7;
设:抛物线的表达式为:y2=a(x﹣m)2+n,
∵顶点为(6,1),则函数表达式为:y2=a(x﹣6)2+1,
把点(3,4)代入上式得:
4=a(3﹣6)2+1,解得:a=,
则抛物线的表达式为:y2=(x﹣6)2+1,
∴y1﹣y2=x+7﹣(x﹣6)2﹣1=﹣(x﹣5)2+,
∵﹣<0,
∴x=5时,函数取得最大值,最大值为元,
故:5月份销售这种鲜花,单株获利最大,最大值为元.
14.(1)当和时,和;(2)当t为55天时,w最大,最大值为180250元.
【详解】(1)当时,设y与t的函数关系式为产.
依题意得:,解得:
与t的函数关系式为.
当时,设y与x的函数关系式为.
依题意得:,解得:
与t的函数关系式为.
当和时,
y与t的函数关系式分别为和.
(2)由题意得,当时,
,当时,(元)
当时,
,当时,
综上所述,当t为55天时,w最大,最大值为180250元.
同课章节目录
